3 Ықтималдықтарды көбейту теоремасы

Теорема. Екі тәуелді оқиға көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығын сол оқиға пайда болды деп алынғандағы екінші оқиғаның шартты ықтималдығына көбейткенге тең:

(1)

немесе

(1^/)

Мысал. М О С К В А сөзін құрастыратын кеспе әріптер әбден араластырылып, 4 кеспе әріпті қатарынан қойғанда К В А С сөзінің шығу ықтималдығын анықтау керек.

Шешуі: Бірінші алынған кеспе әріп К болуы А₁ оқиғасы болсын, екіншісі В болуы –А₂, үшіншісі А болуы –А₃, төртіншісі С болуы А₄ оқиғасы болсын десек, онда КВАС сөзінің пайда болуы А оқиғасы болады. Көбейту теоремасы бойынша

болып шығады.

Теорема. Екі тәуелсіз оқиғалар көбейтіндісінің ықтималдығы олардың шартсыз ықтималдықтарының көбейтіндісіне тең, яғни

болады.

4 Дәріс . Ең болмағанда бір оқиғаның пайда болуының ықтималдығы

1. Ықтималдықтарды қосудың жалпы теоремасы

2. Ықтималдықтың толық (орта) формуласы

3. Байес формуласы

1. Ықтималдықтарды қосудың жалпы теоремасы

Теорема. Екі оқиғаның кемінде біреуінің пайда болу ықтималдығы олардың ықтималдықтарының қосындысынан оқиғалардың бірден пайда болу ықтималдығын шегерткенге тең болады.

(1)

Мысал. Колодада 36 карта бар. Кездейсоқ алынған бір картаның көзір немесе тұз болу ықтималдығын анықтау керек.

Шешуі: Шыққан картаның көзір болуы А оқиғасы, тұз болуы В оқиғасы болсын. Сонда көзір тұздың шығуы АВ оқиғасы болады. Мұның ықтималдығы

А және В оқиғалары үйлесімді, өйткені көзір карта тұз болуы да мүмкін. Олай болса,

немесе 33,3%, өйткені

2. Ықтималдықтың толық (орта) формуласы

Айталық, Н₁, Н₂, ...,Н_п оқиғалары қос-қостан үйлесімсіз оқиғалардың толық тобын құрайтын болсын. Ал В оқиғасы осы оқиғалардың тек біреуімен ғана бірігіп орындалады дейік. Оның үстіне р(Н₁), р(Н₂), ...,р(Н_п) және ықтималдықтары белгілі болсын. Осы берілгендер бойынша В оқиғасының ықтималдығын анықтауға бола ма және ол неге тең деген сұрақ туады. Мұның жауабын ықтималдықтың толық формуласы береді.

Шынында,

(1)

Ал Н₁, Н₂, ...,Н_п қос-қостан үйлесімсіз болғандықтан, оқиғалары да қос-қостан үйлесімсіз. Олай болса, бұл оқиғаларға қосу теоремасын қолдануға болады. Сонда

шығады.

Көбейту теоремасы бойынша

болады.

Демек,

немесе

(2)

жоғарыдағы берілгендері бойынша В-нің ықтималдығын осы (2) формуламен анықтайды. Бұл формуланы ықтималдықтардың толық формуласы деп атайды. Әдетте, Н₁, Н₂, ...,Н_п оқиғаларын гипотезалар (болжамдар) деп атайды.

Байес формуласы

Осы уақытқа дейін қарастырып келген ықтималдықтар интуитивті түрде теориялық болжамдарға сүйеніп, тәжірибе жүргізбей-ақ, комплекс шарт жөніндегі білім (түсінік) негізінде анықталып келді. Тәжірибеге дейінгі Н₁, Н₂, ...,Н_п гипотезалар (оқиғалар) ықтималдығы сәйкес түрде р(Н₁), р(Н₂), ...,р(Н_п) болатынды.

Тәжірибе жүргізілді делік, соның нәтижесінде В оқиғасының пайда болғаны анықталды, енді осы В оқиғасының пайда болуына байланысты Н₁, Н₂, ...,Н_п гипотезаларының ықтималдығын қайта қарауға тура келеді. Яғни ықтималдықтар мәнін анықтауға тіреледі. Бұл ықтималдықты анықтау үшін, көбейту теоремасы мен ықтималдықтардың толық формуласын пайдаланамыз.

Тәуелді оқиғалар В мен үшін

(1)

Бұдан

(2)

шығады. Бұл формулаға толық ықтималдық формуласынан мәнін қойсақ, онда

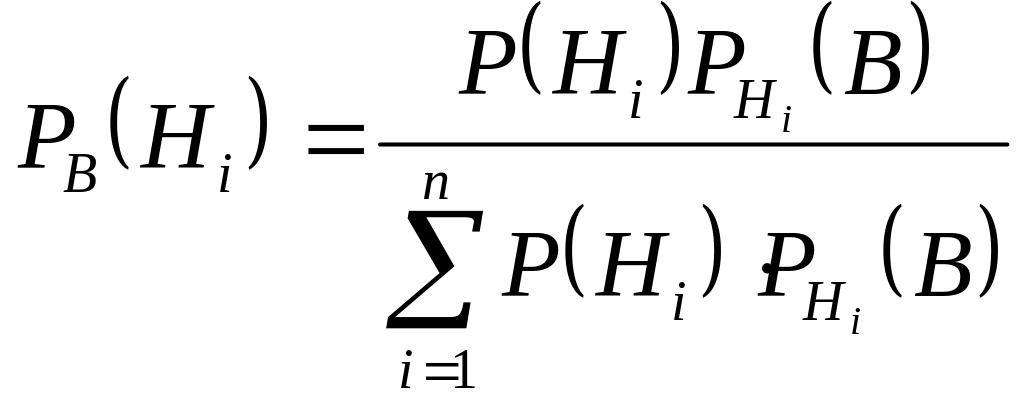(3)

шығады. Осы (3) формуланы Байес формуласы деп айтады.