Мысал-17. Iрiктеудi статистикалық үлестiрiлу мынандай болады:

	17	18	19	20	21	22 .	23
	7	7	3	1	3	2	2

олардың белгiсiнiң салыстырмалы жиiлiктерiнiң үлестiрiлуiн Х түрге келеді:

	17	18	19	20	21	22	23
	0,28	0,28	0,12	0,04	0,12	0,08	0,08

Мiнездеменi табамыз

Белгiнiң орташа арифметикалық ортасын X формула бойынша табамыз: - нұсқанын шарты.

тең болсын , онда .

Х дисперсиясы мынаған тең ,

Онда және варияциясынын коэффициенті мынаған тең:

Мысал-18. Кездейсоқ үйреншiктi емес таңдаулы бөлшектің ықтималдығы 0, 2 тең . кездейсоқ алынған 600 бөлшектерiнің арасында қалыпсыз бөлшегiнің пайда болуы ықтималдығынан салыстырмалы жиiлiгi абсолюттiк шама бойынша 0, 05 тен аспайтын қапылыста қисайтуға кеткен ықтималдығы қандай?

Шешуі: шарт бойынша . табу керек. формуланы қолдану арқылы табамыз. Лаплас функцияларының мәнiн кесте арқылы Ф (3,06)алып, ол 0,49888 тең. Онда .

Мысал-19. Қатенi iрiктеуге кепiлдiк беретін қажеттi нақты көлемдi бөлшектердi анықтаймыз (абсолют А оқиғаның пайда болуының ықтималдығынан, салыстырмалы жиiлiктiң ауытқуы, шамаға байланысты), егер ақаулы бөлшектiң пайда болу ықтималдығы 0, 2 тең екені белгiлi болса.

Шешуі: шарт бойынша . Тартып алынған п бөлшектердiң санын табуға керек болады. Мына формуламен табатын болсақ ,алатынымыз . осыдан

Лаплас функцияларының мәнiн кесте арқылы аламыз: _{. осыдан . Демек, 144 бөлшекті тартып алуға керек.}

&&&

$$$003-002-000$3.3.13

№13 практикалық сабаққа әдістемелік нұсқау

Мысал-20. Бөлшектердi партиясы берілген. Егер көлемнiң iрiктеуі п = 625 тең стандартты емес 40 бөлшекті айкын болса брак санын айкындайсыз . Сенiмдi ықтималдықпен 0,95 шекараны табамыз,мұнда барлық партияда брактiң пайызы жасалған.

Шешуі: Шарт бойынша . Шектi қателiктiң есептеулерi үшiн, кепiлдiк берiлген ықтималдықты 0,95ті деген салыстырмалы жиiлiкпен оқиғаның пайда болу А жағдайы мен белгiсiз ықтималдықты алмастырамыз.

0,064. Онда . Мына формуланы колдану арқылы:

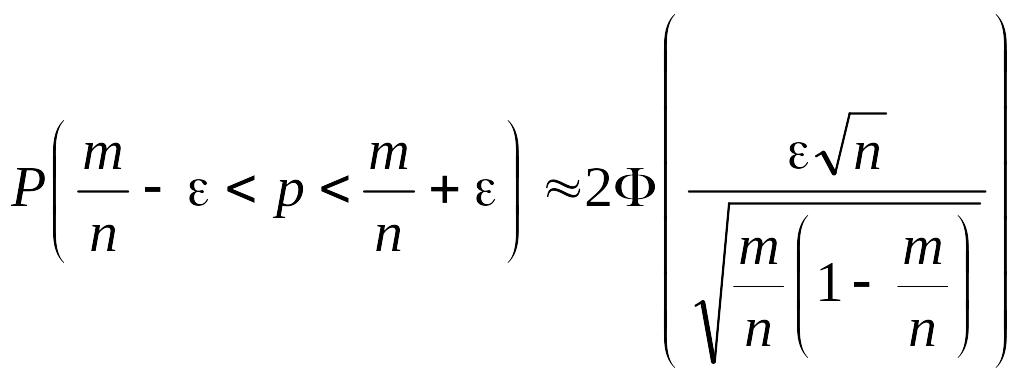
табатынымыз, . Мұндағы . Лаплас функцияларының мәнiн кесте арқылы аламыз: .

бұдан табамыз.

Осы арқылы: _{тең болады.}

_{Сонымен} 6,2% < р <6,6%.

&&&

$$$003-002-000$3.3.14 Сенімділік интервалы

№14 практикалық сабаққа әдістемелік нұсқау

Мысал-21. Көлемi п=25 iрiктеуi бойынша жасалған белдiкшелердiң үлкен партиясынан iшiнара орташа арифметикалық диаметрi 10 мм ге тең белдiкше табылған. Х- белдікшенің диаметрі кез келген алынған көлем деп алсақ, сенімді интегралды табамыз,ал ол 0,99 сенімді ықтималдықпен диаметрі а белдікшені белгісіз математикалық күтіммен басады.

Шешуі: есептің шарты бойынша . Біздің жағдайымызда белгілі, онда а пареметірді бағалау мына шартпен жүзеге асады: _{, шарттан} t _{белгiсiз мәнді аламыз. Ф(t ) мәндердiң кестесi бойынша t = 2, 58 табамыз. Онда бағалау тура: болады. Демек, iзделетiн сенiмдi интервал}

9,95 < а < 10,05. _{тең болады.}

&&&

$$$003-002-000$3.3.15 Регрессия теңдеуін құру

№15 практикалық сабаққа әдістемелік нұсқау

Мысал-22. Бақылау аймақтарында 10 сынау жүргізілген. Сынау нәтижелері кестеде берілген.

	6	11	11	7	8	10	12	6	10	9
	27	32	33	30	30	33	34	29	31	32

Мұндағы:

X – т/га тыңайтқыш мөлшері, Y - ц/га жиналған өнім.

Y тің Xке регрессияның түзу сызығының iшiнара теңдеудi табамыз

Шешуі: Өнiмдiктiң жоғарылатуына тыңайтқыштардың үлкеюiн ықпалды енгiзудi қарап шығамыз. Оқылытын белгiлердiң арасындағы байланыс Yның регрессиясының түзу сызығы теңдеумен X-қа бейнелене алады:

_{А және Bның параметрлерiнiң есептеулерi үшiн есептi кестенi құраймыз:}

№ бақылау
1	27	6	36	162
2	32	11	121	352
3	33	11	121	363
4	30	7	49	210
5	30	8	64	240
6	33	10	100	330
7	34	12	144	408
8	28	6	36	168
9	31	10	100	310
10	32	9	81	288

Ізделінді ажәне b параметрларын төмендегі жүйеден таба аламыз:

Демек .

Онда берілген кореляциялық кесте бойынша Х-ке Y регрессиясының теңдеуі мына түрде болады: .