2. Математикалық күтім, дисперсия және орта квадраттық ауытқу

№6 практикалық сабаққа әдістемелік нұсқау

Мысал-6. Х дискреттi кездейсоқ мәнi келесi ықтималдықтардың үлестiрiлу кестесiмен берiлген:

	2	5	8	9
	0,1	0,4	0,3	0,2

табайық.

Шешуі: Өйткенi ықтималдықтардың үлестiрiлу кестесi белгiлi, онда

• табу үшін алдымен 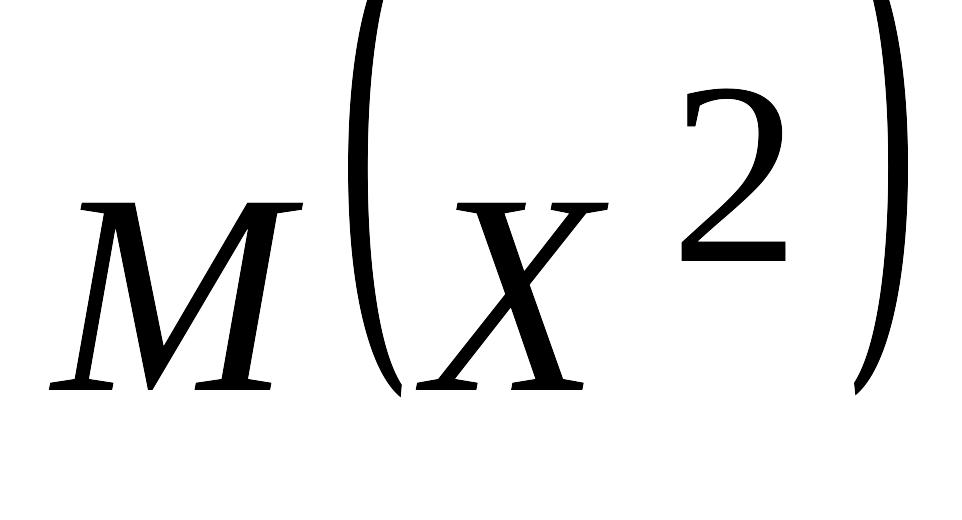табу керек

Сонда

, .

&&&

$$$003-002-000$3.3.7 Үзіліссіз кездейсоқ шама. Үлестіру функциясы және тығыздық

№7 практикалық сабаққа әдістемелік нұсқау

Мысал-7. Егер 100 билет алса, әрбiр лотереялық билеттердiң ұтыстының ықтималдығының дисперсиялары 0,05 тең. Математикалық күтімді және Лотереялық билеттің дисперсиясын табамыз

Шешуі: . Х – ұтып алынған лотереялық билеттердiң саны болсын. Кездейсоқ мәндi Х олардың биномиалды үлестiрiлуi болады, қарастырылып отырған есеп Бернулли схемасын қанағаттандырады. Сондықтан

.

&&&

$$$003-002-000$3.3.8 Дискреттi кездейсоқ үлестірім заңы

№8 практикалық сабаққа әдістемелік нұсқау

Мысал-8. Х дискреттi кездейсоқ мәнi келесi ықтималдықтардың үлестiрiлу кестесiмен берiлген:

	1	2	3	4	5
	0,1	0,15	0,2	0,35	0,2

Интегралдық функцияның үлестірілуін тап.

Шешуі: Дискреттi кездейсоқ мән үшiн

Егер онда

Егер онда

Егер онда

Егер онда

Егер онда

Егер онда

Сайып келгенде,

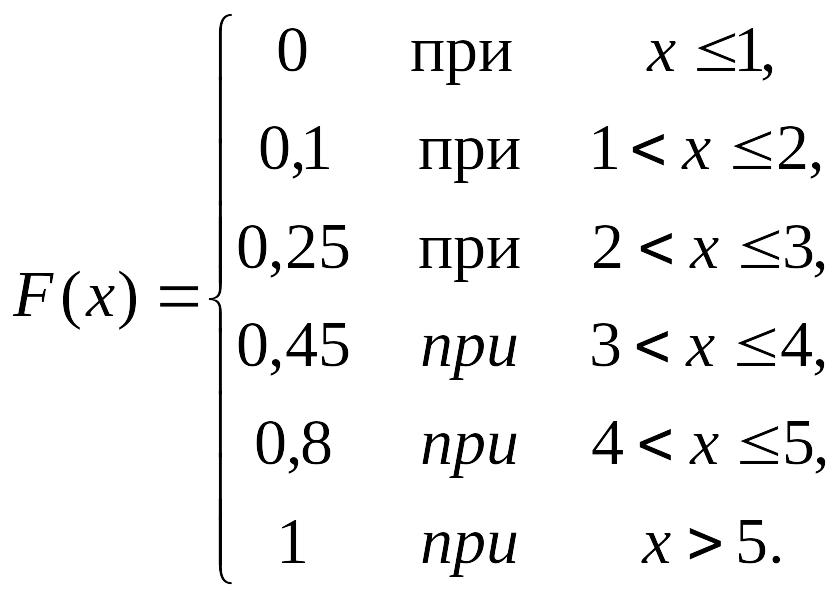
Мысал-9. Математикалық күтiм және кездейсоқ мәннiң х дисперсиясын тап,интегралдық функциямен берілген.

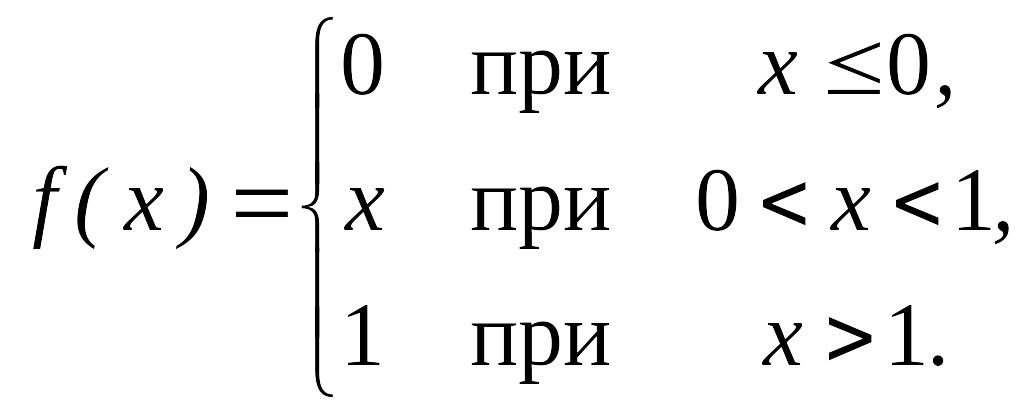
Шешуі: Дифференциалдық функцияны табамыз:

Математикалық күтімді табамыз

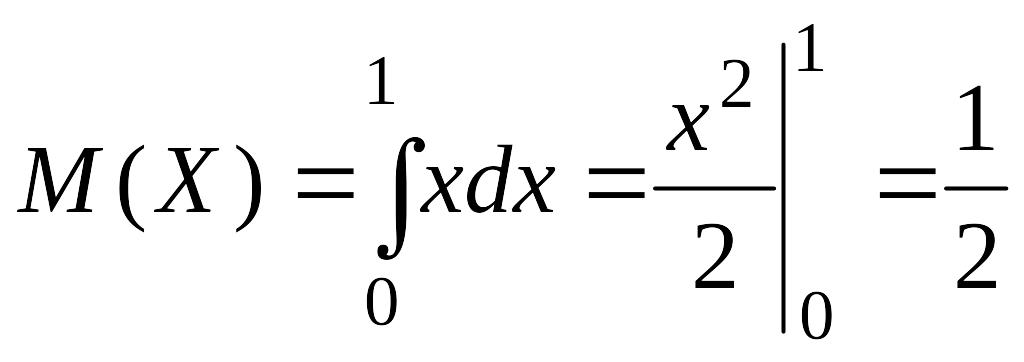
Дисперсиясын табамыз:

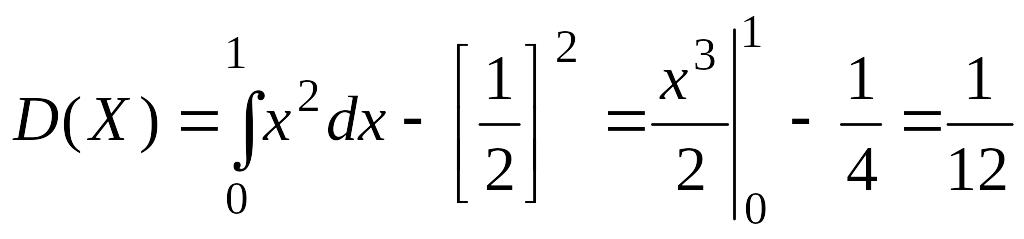
Мысал-10. Х кездейсоқ мәнi нормалдың таратылу заңының математикалық күтіммен үлестiрiлулері 3 – ке тең, және 4-шi дисперсиясымен. Ықтималдықтар тығыздығы үшiн кездейсоқ шамаларды табамыз.

Кездейсоқ мәннiң ықтималдығының тығыздығы Х мына турде алынады

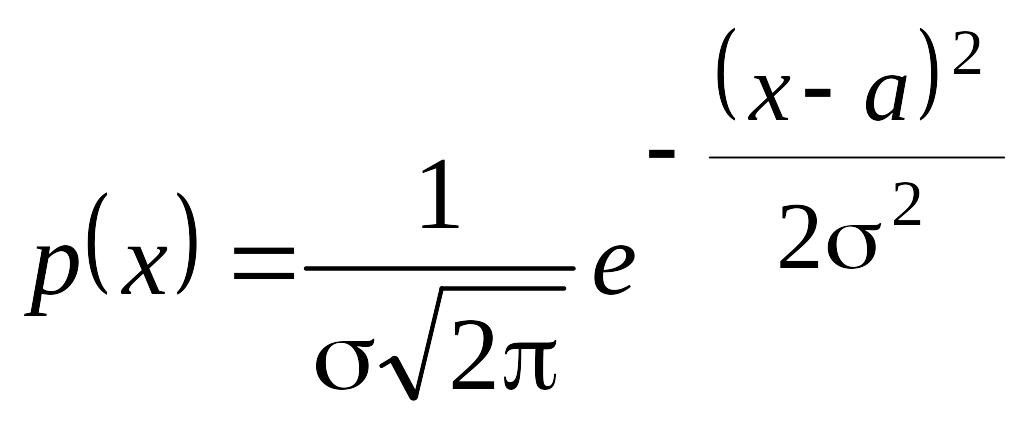
Есеп шартты бойынша тең.

&&&

$$$003-002-000$3.3.9 Қалыпты үлсетіру заңы

№9 практикалық сабаққа әдістемелік нұсқау

Мысал-11. Құрал қызметінің мерзiмi кездейсоқ мәндi,қалыпты үлестіру заңына бағынады, 15 жыл кепілдікпен және орташа квадраттылық ауытқуымен 3 жылдарға тең. 10 жыл мен 20 жыл аралығындағы уақытта . құрал қызмет ету ықтималдығын анықтаймыз.

Шешуі: Есеп шартты бойынша: . Табу керек . мына формуланы қоя отырып - ті аламыз.

Лаплас функциясының кестелерiнен мына мәнді табамыз. Демек шығады.

Мысал-12. Зауытта шығарылатын консерва банкаларының салмағы орташа салмақпен алғанда нормальды үлестiрiлуiнің заңына байланысты 250 г. және орташа квадраттылық ауытқуы 5г. Орта салмақпен алганда абсолюттiк шаманың банкалардың салмағынан 8 г. ықтималдық ауытқуын анықтаймыз.

Шешуі: Есеп шартты бойынша , . Оқиғалар ықтималдығын табуға керек . осы формуланы қолдана отырып мына формуланы аламыз.

Лаплас функциясының кестелерiнен мына мәнді табамыз. Демек .

Мысал-13. Нысаналар бойынша атыстың жанында, нысананың ортасынан ауытқудың 30 см, артық-кемiн радиустың шеңберi ұсынатын өзiменмен 6см тең. Чебышевтiң леммасын пайдалана отырып, нысананың ұтылуы ықтималдығын бiр атыста бағалаймыз. Шешiм. Егер оқиға болса , нысананы шалдықтырады. ауытқудың ортасынан Нысанаға дейін артық-кемi тең. Онда формула бойынша алатынымыз,

Mысал-14. Бөлшектер партиясы дайындалды. Бөлшектiң орташа ұзындығының мәнi 50cм ге тең, орташа квадраттық ауытқу 0, 2 тең кездейсоқ алған бөлшектiң ықтималдығы және оның ұзындығы кемiнде 49, 5 см болатын және 50, 5 см аспайтын болу керек екенін бағалаймыз.

Шешiм. Холардың кездейсоқ мәнi - бөлшектi ұзындық - математикалық күтiм де түпкi дисперсиясы болады. Демек, қаралатын оқиғаның ықтималдығы бағалау үшiн астыдан Чебышевтiң теңсiздiгi қолданамыз. Теңсіздіктен шығатыны, , онда

.

болғандықтан

.

&&&

$$$003-002-000$3.3.10 Чебышев теоремасы

№10 практикалық сабаққа әдістемелік нұсқау

Mысал-15. 4-шi 1000 тәуелсiз кездейсоқ мәндердiң әрбiрi дисперсия. Ықтималдық абсолюттiк шама олардың математикалық күтiмдерiнiң орташа арифметикалығы бұл кездейсоқ мәндердiң орташа арифметикалығының ауытқу 0,2 шектен шықпаған бағалаймыз.

Шешуi: Қаралатын кездейсоқ мәндердiң тiзбектерiне Чебышевтiң теоремасын қолдануға болады, өйткенi: 1) тәуелсiз шама, 2) дисперсиялар шектелген: 3) математикалық күтiмдер бар болады. Iзделiпіп отырған теңсiздiктi былай бағалап, пайдалана аламыз,

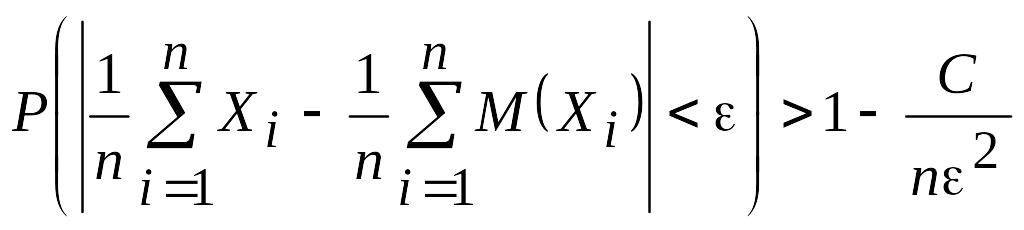
мұндағы , : .

&&&

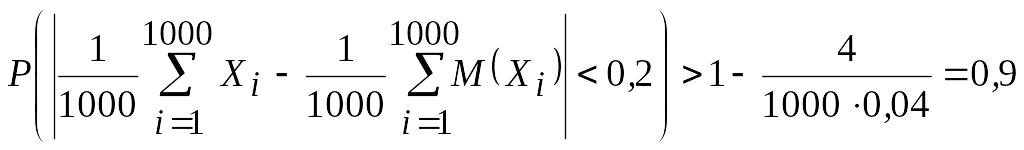$$$003-002-000$3.3.11 Математикалық статистика

№11 практикалық сабаққа әдістемелік нұсқау

Мысал-16. Сұрау жолымен бiрiншi курстiң 25 студенттерiнiң (толық жылдардың саны) жас шамасы туралы келесi мәлiметтер алынған:

18,	17,	23,	18,	17,
19,	18,	20,	17,	22,
19,	21,	18,	18,	17,
22,	18,	21,	17,	21,
18,	19,	17,	23,	17.

Жас шамасы бойынша студенттердiң статистикалық үлестiрiлуiн құраймыз. Құлашты өзгертудi табамыз, жиiлiктердiң полигоны құрастырамыз және салыстырмалы жиiлiктердiң үлестiрiлуiн де қатар құраймыз .

Шешуi: Iрiктеудi статистикалық үлестiрiлудi бастапқы деректерді қолдану арқылы құраймыз.

	17 .	18	19	20	21	22	23
	7	7	3	1	3	2	2

Өзгертудi құлаш сонда болады: R = 23-17=6.

Жиiлiктердiң полигоны құрастыру үшiн,болуы мүмкiн белгiнiң мәндерi және алған нүктелерден абсциссаларды өстерiне бөлiп шығарып қоямыз биiктiктiң перпендикулярларын қалпына келтiремiз. 1-шi сурет кесiндiлердiң перпендикулярлары осыдан кейiн дәйектi түрде қарасырамыз.)

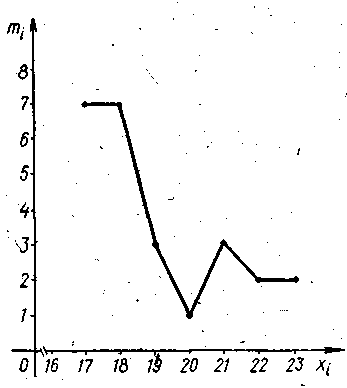
Белгiнiң мәнiнiң салыстырмалы жиiлiктерi X, содан соң табатынымыз салыстырмалы жиiлiктердiң үлестiрiлуi мына қатарды құраймыз:

	17	18	19	20	21	22	23
	0,28	0,28	0,12	0,04	0,12	0,08	0,08

&&&

$$$003-002-000$3.3.12 Статистикалық таңдама

№12 практикалық сабаққа әдістемелік нұсқау