Эмпирикалық үлестірудің қалыпты ауытқуын бағалау. Ассиметрия және эксцесс.

Қалыпты үлестіруден өзгеше үлестіруді оқығанда олардың айырмашылығын сандық бағалау қажеттігі туады. Сол мақсат үшін арнайы сипаттама енгізіледі, дербес жағдайда ассимметрия және эксцесс ұғымы енгізіледі. Қалыпты үлестіру үшін бұл сипаттамалар нөльге тең. Сондықтан, тексеріп отырған үлестіру ассимериясы және эксцессі аз ғана мән қабылдаса, онда бұл үлестірудің қалыптыға жақын екенін байқауға болады. керісінше, ассимметрия мен эксцесс үлкен мәнді болса, оның қалыпты үлестіруден көп ауытқитынын көрсетеді.

Теориялық үлестірудің ассимметриясы деп үшінші ретті орталық моменттің орташа квадраттық ауытқудың кубына қатынасын айтады.

Егер үлестіру қисығының «ұзын бөлігі» математикалық күтімнің оң жағында жатса, ассимметрия оң болады, ал егер «ұзын бөлігі» сол жағында жатса, ассиметрия теріс болады.

Практикада ассиметрияның таңбасын үлестіру қисығының модаға қарағанда орналасуына қарап анықтайды (дифференциалдық функцияның максимум нүктесі) «Тіктігін» бағалау үшін, яғни теориялық үлестіру сызығының қалыпты қисықпен салыстырғанда аз немесе көп көтеріңкі болатынын бағалау үшін эксцесс деген сипаттамамен пайдаланады.

Теориялық үлестірудің эксцессі деп теңдігімен анықталатын сипаттаманы айтады. Қалыпты үлестіру үшін болғандықтан, эксцесс нөльге тең болады.

Егер эксцесс оң болса, онда қалыпты қисыққа қарағанда қисықтың биік және «үшкір» төбесі болады. Егер эксцесс теріс болса, қалыпты қисыққа қарағанда салыстырып отырған қисық төмен және «жазық» төбелі болады.

Эмпирикалық үлестірудің ассиметриясы теңдігімен анықталады, мұндағы - үшінші ретті орталық эмпирикалық момент.

Эмпирикалық үлестірудің эксцессі теңдігімен анықталады, мұндағы - төртінші ретті орталық эмпирикалық момент.

және моменттерді көбейту әдісімен және қосынды әдісімен төмендегі формулалар арқылы табады.

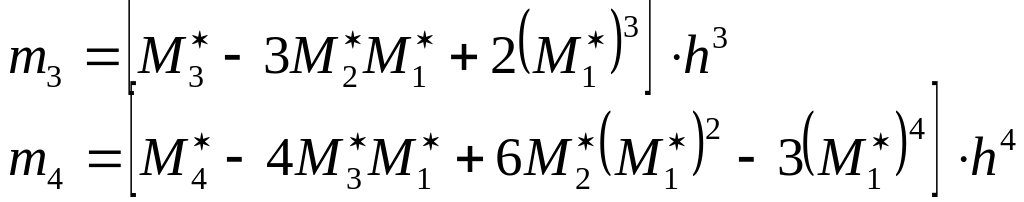
3 Практикалық сабақтар

Практикалық сабақ

&&&

$$$003-001-000$3.3.1 Комбинаторика элементтері.

&&&

$$$003-001-001$3.3.1.1 №1 практикалық сабаққа әдістемелік нұсқау

Мысал

Мысал-1 . А={1; 2; 3; 4; 5} жиыны берілген. А жиынының элементтерін қалданып неше тәсілмен а) бір орынды; б) екі орынды; в) үш орынды; г) төрт орынды санды құруға болады? (цифрлары қайталанбайтын болса)

Шешуі: а) Бір орынды санды бес тәсілмен алуға болатыны анық көрініп тұр:1, 2, 3, 4, 5. Шындығында, 5 элементтен 1 элемент алу, демек = бір орынды сан.

б) Екі орынды сан - 5 элементтен 2 элемент алу (алмастыру), = екі орынды сан.

в) = үш орынды сан.

г)

Мысал-2. Төрт оқушы емтихан тапсыруда. Егер олардың ешқайсысына «қанағаттанарлықсыз» бағасы қойылмайтын болса, онда төрт бала емтихан тапсырмайды.Неше әдіспен баға қоюға болады, егер оларға қанағаттандырмайтын баға қойылатын болса?

Шешуі: Әрбір студент «өте жақсы», «жақсы», «қанағаттандырады» деген бағалардың арқайсысын алуы мүмкін. Қарастырып отырған көпмүшеміз 3 түлі элементтен тұрады. Демек, үш қайталаудан төрт элемент қайталанды. Ал олардың саны .

&&&

$$$003-002-000$3.3.2 Ықтималдықты табуда комбинаторика элементтерін пайдалану

№2 практикалық сабаққа әдістемелік нұсқау

Мысал-2. 15 ұл баладан 5 қыз баладан құралған туристік группада шаруашылық командасын құру керек болады.Жребие арқылы шаруашылық командасына 4 адамнан бөлді. Бұл команданың құрамында екi ұл бала және екi қыз бала болу ықтималдығын тап?

Шешуі: Сынаудың басты мақсаты, 20 адамдардың ішінен 4 адам таңдап алу. Таңдау жеребе бойынша iске асады, сонда сынаудың барлық нәтижелерi бiрдей ықтималдықпен және бұдан басқа, олар үйлеспейді. Сынаудың нәтижелерiнiң саны , комбинациясы төрт элементтерден және комбинациялардағы олардың орналастырылуының реті есепке алынбайды. А оқиғасындағы құрамда екi ұл бала және екi қыз бала болатын болсын. 15 ұл баланың ішінде екі ұл баланы былай таңдап лауға болады, өйткенi комбинация 4 элементтен тұрады және комбинацияның реті есептелмейді. А оқиғасында 2 ұл бала, 2 қыз бала бир құрамда болсын. 15 ұлдан еки ұлды , 2 қыз баладан 5 рет таңдап алуға болады. А оқиға шығармаларының ережесі бойынша сынаудың нәтижелерiне жағдай жасайды. Ізделiп отырған ықтималдық (1) формула бойынша есептелінедi және

тең болады.

&&&

$$$003-002-000$3.3.3 Ықтималдықтың қосу және көбейту теоремалары

№3 практикалық сабаққа әдістемелік нұсқау

Мысал-3. Екi қораптарда бiрдей шамамен және бірдей формадағы қарындаштар жатыр, бiрақ әртүрлi түсті. Бiрiншi қорапта 4 қызыл және 6 қара, екiншi 3 қызыл, 5 көк және 2 қара. Екi қораптан да қарындаштар бiр-бiрден жорамалдап суырылады. Екi қарындашта қызыл болатындығының ықтималдығы қандай?

Шешуі: Сынаудың басты мақсаты әрбiр қораптан бiр-бiрден қарындаш суырылып тұрады. А оқиғасында бірінші қораптан суырылып алған қарындаш қызыл, В оқиғасында екінші қораптан суырылып алған қарындаш та қызыл болсын. АВ оқиғаларындағы екі қарандашта қызыл. А және В оқиғалары тәуелсiз болады, онда . А және В оқиғалар ықтималдығы сәйкесiнше тең , . Демек, ықтималдығы , екi қарындаш қызыл екенін көрсетеді, тең .

&&&

$$$003-002-000$3.3.4 Толық ықтималдықтың формуласы.

№4 практикалық сабаққа әдістемелік нұсқау

Мысал-4. Сәйкесiнше 20, 30 және 50 даналарға жететiн радио шамдардың үш партиялары болады. Радио шамдардың қанша уақыт жұмыс істейтіндігінің ықтималдығын тап, сәйкесінше партияларға 0,7, 0,8 және 0,9 – ға тең. Кездейсоқ таңдалған жүз шамның қайсысы айтылған уақытта жұмыс жасайды?

Шешуі: Тәжірбиенің басты мақсаты 100 шамнан біреуі ғана сатті болуы. А оқиғасындағы суырылған шам айтылған уақытта жұмыс жасауының ықтималдығын есепте. Егер сәтілікке таңдалған бірінші, екінші, үшінші партияларының гипотездеріне сәйкес болсын. Классикалық ықтималдықтардың формуласы бойынша: , , .

Есептің шарты бойынша , , .

Толық ықтималдықтың формуласы бойынша А оқиғасының ықтималдығы мынаған тең

&&&

$$$003-002-000$3.3.5 Сынауды қайталау.

№5 практикалық сабаққа әдістемелік нұсқау

Мысал-5. Ақшалай - болжағыш лотерея билетiнің бiр-бiрден ұтыс ықтималдығы 0,2 тең. Алты рет алынған билеттің екеуі ұтымды болу ықтималдығы қандай?

Шешуі: Тәжiрибиеде дәйектi түрде 6 билет тексеріліп тұрады, яғни 6 рет қайтадан тәуелсiз сынаулар жүргiзiледi. Әрбір тәжірбиеде 2 нәтиже болады: билет ұтымды және билет ұтымсыз болады. Әрбiр сынаудағы ұтыстың ықтималдығы тұрақты. Демек, Бернулли схемасы орындалады. оқиғасы мейлi 2 билет ұтымды екенін көрсететiнен тұрады. Бернулли формуласы бойынша онда:

тең болады.

&&&

$$$003-002-000$3.3.6 Кездейсоқ шама. Дискретті кездейсоқ шама.