15 Дәріс. Корреляциялық және регрессиялық талдау элементтері. Сызықтық және сызықтық емес корреляциялық регрессия теңдеуі Эмпирикалық және теориялық жиілік Дискретті үлестіру

1. Дискретті үлестіру

2. Эмпирикалық үлестірудің қалыпты ауытқуын бағалау. Ассиметрия және эксцесс.

Үлестіру заңы белгісіз, Х дискретті кездейсоқ шаманы қарастырайық. Айталық, п сынпау жүргізгенде кездейсоқ шама Х мәнін рет, мәнін рет,..., мәнін рет алсын, әрі болсын.

Эмпирикалық жиілік деп нақты бақыланатын жиілік -ді айтады.

Қарастырып отырған Х шама белгілі бір заңмен үлестірілген деп жорамалдайтын негіз бар болсын.

Сол жорамалдау берілген бақылаумен үйлесетінін тексеру үшін, бақыланатын мәндердің жиілігін есептейміз, яғни Х шаманың әрбір қабылдайтын мәндерін теориялық түрде қанша реттен қабылдайтынын есептейміз, егер ол болжам отырған заңмен үлестірілсе.

Нақтылы бақыланатын эмпирикалық жиіліктен өзгеше, теориялық есептеу арқылы табылатын жиілігін теңестіретін (теориялық) жиілік деп атаймыз.

Теңестіретін жиілікті теңдігінен табамыз, мұндағы -сынау саны, - Х болжағандай үлестірілді дегендегі мәнін бақылау ықтималдығы.

Мысал. Эксперимент қорытындысында сынау жүргізгенде төмендегідей эмпирикалық үлестіру тіркелген.

Бақылау Мәндері		0	1	2	3	4	5	6	7
Эмпирикалық жиілік		120	167	130	69	27	5	1	1

Егер кездейсоқ шама Х Пуассон заңымен үлестірілген деп жорып, теңестіруші (теориялық) жиілік -ті табайық.

Шешуі: Пуассон үлестіруіндегі параметр , сол үлестірудің математикалық күтіміне тең. Математикалық күтімді іріктеме ортасы арқылы бағалайды, олай болса -ны да таңдама ортасы арқылы бағалаймыз. Іріктеме ортасы 1,5-ке тең екенін берілгені бойынша оңай табуға болады. Олай болса, деп алуға болады.

Сонымен Пуассон формуласы

төмендегідей болады. ;

Осы формуланы қолданып, ықтималдығын табамыз.

Егер болса:

Теориялық (теңестіруші жиілікті) табайық. (1-ге дейін жуықтап)

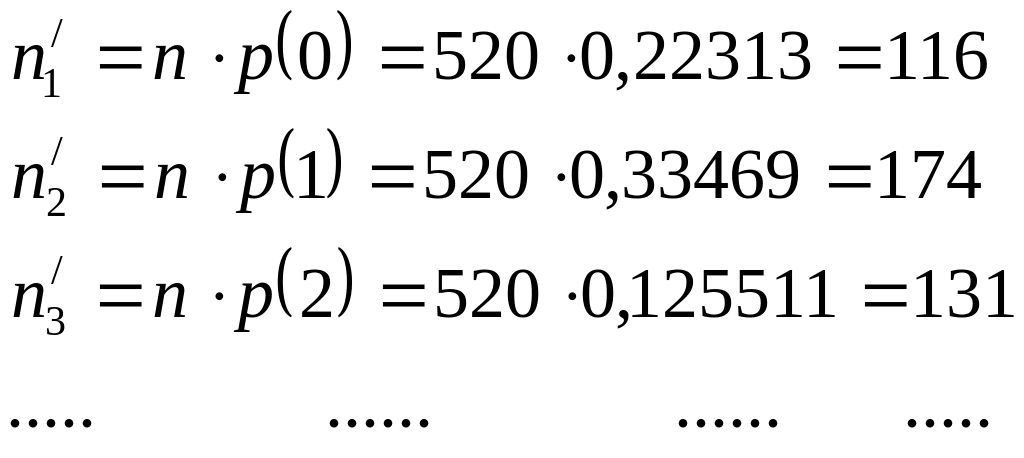
Бақылау Мәндері		0	1	2	3	4	5	6	7
Эмпирикалық жиілік		120	167	130	69	27	5	1	1
Теориялық жиілік		116	174	131	65	25	7	2	0

Эмпирикалық жиілік пен теориялық жиілік арасындағы аз ғана салыстырмалы айырмашылық, қарастырылған үлестіру Пуассон заңына бағынатындығы деген жорамалдың шындыққа жуық екенін дәлелдейді.

Енді таңдама дисперсиясын осы үлестіру бойынша есептесек оның да таңдама ортасына тең екенін, яғни 1,5-ке тең екенін көреміз. Бұл біздің жасаған жорамалымыздың дұрыс екенінің тағы бір дәлелдеуі болады, өйткені Пуассон үлестіруінде .