Эмпирикалық моменттер

Практикада бастапқы төрт моментті қарастырады. Қалған тұрақты А-ға қатысты ретті момент

формуласымен өрнектеледі. болса, бастапқы момент - ты аламыз, Ал болса, центрлік момент - ты аламыз. Олай болса, бастапқы моменттер:

бұдан болғанда

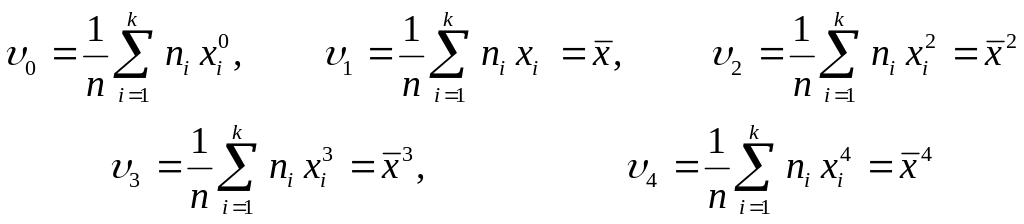
Центрлік моменттер

бұдан болғанда

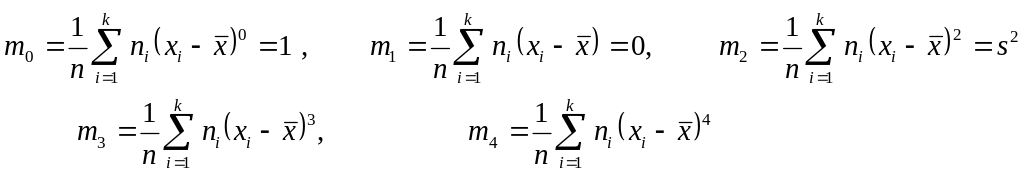
Центрлік моменттерді бастапқы моменттер арқылы есептеуге болады.

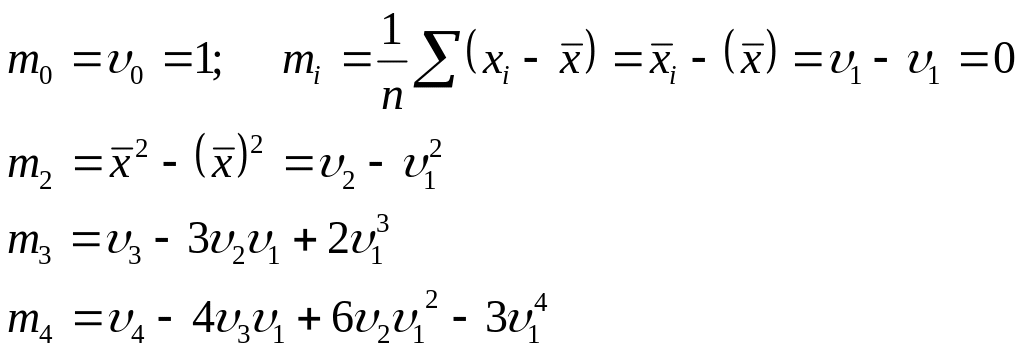
Алғашқы төрт ретті бастапқы моменттерді есептеуге мына кестені пайдаланамыз

...	...	...	...	...	...

Алғашқы төрт ретті центрлік моменттерді есептеуге мына кестені пайдаланамыз

...	...	...	...	...	...	...

Бас жиын үлестіруі параметрлерін бағалау Белгісіз параметрлерді бағалау әдістері

Математикалық статистикада белгісіз параметрлерді бағалау үшін әр түрлі әдістерді пайдаланады, мысалға, байестік әдіс, ең аз квадраттар әдісі, моменттер әдісі, Фишер ұсынған шындыққа максимал ұқсастық принципі т.т. Қазіргі уақытта соңғы әдіске көбірек назар аударып жүр. Ол әдіс арқылы тиімді және қисынды бағалар алады.

Белгісіз параметр -ның бір ғана санымен бағалануының мынадай бір үлкен кемістігі бар: бірнеше параметрлер бойынша қисынды, ығыспаған және тиімді баға талаптарына жауап бере отырып, бұл бағалау бізге бас жиынның параметріне жуықтау дәлдігі мен сенімділігі туралы мәлімет бермейді. Бұл кемістік бақылаулар саны аз болған сайын көзге түсерліктей байқала береді. Сондықтан мұндай кемістік болмау үшін бағалаудың сенімділік интервалы ұғымын енгізеді.

Сенімділік интервалын анықтау үшін әрқайсысы бақылаудан алынған аргументтерінің функциясы болатын кездейсоқ шамаларын табу керек және бұлардан жасалған аралығы Р-дан кем емес ықтималдықпен параметрі мәнін қамтуы қажет. Былайша айтқанда, бұл жерде Р ықтималдықпен теңсіздігі орындалады. Мұндағы - сенімділік интервалының төменгі шекарасы, ал - жоғарғы шекарасы ролін атқарады. Алдағы уақытта Р ықтималдығын сенімділік немесе сенімді ықтималдық деп айтатын боламыз. Бұл жерде сенімділік интервалын максимум ұзындығы маңызды роль атқарады. Мұның жартысы бағалауымыздың дәлдігін сипаттайды. Өйткені интервал ұзындығы қаншалықты кіші болған сайын, яғни кіші болған сайын, параметр -ның бағалануы дәлдене түседі. Айталық,

болсын.

теңсіздігінен немесе теңсіздігі шығады.

Сонда .

Бұл теңдікті былай ұғу керек: интервалының белгісіз параметрдің мәнін қамту ықтималдығы -ға тең. Бұл интервал сенімділік интервалы деп аталады.