Раздел 4. Теория графов
1. Ребра называются смежными, если они
а) инцидентны одной и той же вершине
2. Если две вершины соединены одной дугой, они называются
в) смежными
3. Какие из графов являются подграфами данного графа G
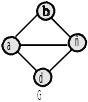
а)
в)
Если любые две вершины графа можно соединить простой цепью, то граф называется:
а) связным;
5. Сколько вершин содержит гамильтонов цикл графа с 5 вершинами?
а) 5
6. Граф содержит 7 дуг. Его эйлеров цикл будет состоять из
б) 7 дуг
7. Эйлеров цикл
а) содержит каждое ребро только один раз;
8. Гамильтонов цикл
б) содержит каждую вершину только один раз;
9. В эйлеровом графе все вершины
а) четной степени;
10. В полуэйлеровом графе допускаются
б) 2 вершины нечетной степени;
12. Какой из циклов графа с множеством вершин {a,b,c,d,e,f} является гамильтоновым?
в) abecdfa
13. Какой граф является гамильтоновым:
б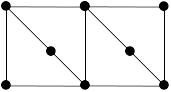
)
в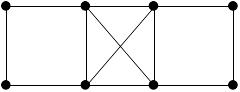
)
14. В алгебраической форме представления графов аксиома о единичном элементе формулируется следующим образом:
г)
15. В алгебраической форме представления графов имеет ли место свойство коммутативности относительно операции конкатенации для ориентированных графов?
б) нет.
16. Правило минимизации фрагмента графа:
а)
;
б)
;
в)
.
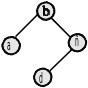
Глубина элемента а2 в дереве
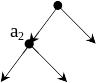равна
б) 1;
Степень вершины а2 в графе равна
г) 3.
32. В графе из n вершин остов содержит:
б) n-1 ребро;
33. Дерево есть:
г) связный граф без циклов.
34. Простая цепь это:
г) маршрут, где нет повторяющихся вершин и ребер.
35. Расстояние между вершинами есть
б) длина кратчайшего пути.
49. Структуры “булев граф” и “булево дерево”:
в) отличаются наличием сходящихся разветвлений
50. Структура “булев граф”
а) имеет сходящиеся разветвления
51. Структура “булево дерево”
б) не имеет сходящихся разветвлений
56.
Множество {0, 1, X,
}
является самым минимальным
теоретико-множественным замкнутым
алфавитом.
а) да
58. Значения функции 2ИЛИ равны соответственно 0-Х-1 при подаче последовательности наборов 0Х-ХХ-Х1:
а) да
67. Сколько кубов содержит минимальная кубическая форма представления сильносвязного графа, имеющего четыре вершины:
а) 16;
68. Количество дуг в графе, определенное кубом LL, равно:
в) 9.
81. Сколько двоичных векторов содержит куб 01X10X10?
в) четыре
82. КП – это минимизированная таблица истинности, записанная в алфавите {0,1,X}
а) да
90. Любой сильносвязный граф может быть представлен одним кубом
а) да