17.Бірінші ретті дербес туындылы теңдеу. Характеристикалары. Үзіліссіздік теңдеуі

Бірінші ретті дербес туындылы теңдеу ұғымы туындыдан кейін пайда болған, яғни XVIII ғасырда қалыптасқан. Бұл теңдеулерді жай дифференциалдық теңдеулер сияқты шешу үшін,оған сәйкес характеристикалық жүйе құрамыз. Сызықты емес бірінші ретті теңдеу келесі түрге ие

(1)

Егер (1) теңдеудің шешіміu(x) болса,онда 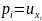функциясы квазисызықты емес теңдеуді қанағаттандырады. Біз функциясын екі рет үзіліссіз дифференциалдасақ (1) теңдеудің u(x) шешімі мына түрге келеді

.

теңдеуін бойынша дифференциалдасақ

-ға қатысты квазисызықты теңдеу аламыз

Бұл теңдеу үшін характеристикалық жүйе келесі түрге ие

Әрбір үшін алынған характеристикалық теңдеулерді біріктірсек келесі теңдеулер алынады

,

Енді u-ға қатысты теңдеуді алу керек ол үшін u(x) функциясынан жүйесіне қатысты туынды аламыз:

Сонымен , 2n+1 теңдеуі үшін алынған

(4)

Жүйесі (1) cызықты емес теңдеу үшін характеристикалық жүйе болып табылады.

Үзіліссіздік теңдеуі

Бұл теңдеу негізінен тұтас орта механикасында қарастырылып,сұйықтың немесе газдың қозғалысын сипаттайды.Сұйықтың қозғалысының жылдамдық векторын былай өрнектейік:

, ал оның тығыздығы.

Таңдалған облысты деп алайық. t уақыт моментінде сұйықтың массасы

(1)

формуласымен анықталады,мұндағы массаның өзгеру жылдамдығы шамасына тең. массаның өзгерісі тек қарастырылып отырған шекарасы аркылы сұйықтың ағып келуі мен ағып шығуына байланысты,яғни массаның өзгеру жылдамдығы 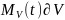сұйық ағынына тең.

. (2)

Мұндағы жылдамдық векторы мен нормальдың скаляр көбейтіндісі x V,d V-ға түсірілген аудан. Сонда

- (3)

теңдіктің оң жағын Гаусс-Остроградский түрлендіруіне келтіреміз

(4)

мұндағы div-кеңістіктегі айнымалылар

бойынша дивергенция операторы. Бұл теңдіктен гидродинамикадағы үзіліссіздік теңдеуін аламыз

(5)

18.Бірінші ретті дербес туындылы теңдеу. Характеристикалары.

Анықтама:

= 0 (1)

теңдеуін бірінші ретті дербес туындылы теңдеу деп атайды, егер

шарты кейбір G ашық көпмүшелікте және айнымалылар кеңістігіде орындалса.

(1)- теңдеудің классикалық шешімі деп сол теңдікке қойғанда дұрыс шешімін беретін үзіліссіз функциясын айтамыз.

Х кеңістігінде тегіс гипержазықтық , анықталған және осы гипержазықтықта функциясы берілген.

Анықтама:

(1)- теңдеу үшін Коши есебі деп осы теңдеудің шешімін табуға арналған есепті айтамыз, егер ол бастапқы шартын қанағаттандырса.

Судың құмға сіңу теңдеуі.

Су тек ауырлық күші әсерінен қозғалады деп қарастырайық, яғни тек қана вертикаль қозғалыс болады және қозғалыс горизонталь координатаға тәуелді емес. Шығу және кіру көздері болмағандықтан судың сіңу жылдамдығы тығыздық функциясымен мына түрде анықталады:

яғни

Тәжірбиеде анықталған тәуелділігі 1 –суретте көрсетілген.

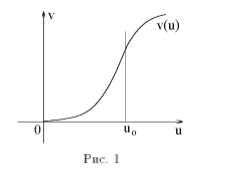
аралығында нақ дәлділікпен бұл тәуелділіктің параболалық тип екенін көрсетуге болады, яғни .

Қарастырылып отырған бірмәнді жағдайда теңдеуі мына түрге келеді:

әлде

;

мұндағы

.

Тәжірбиеде табылған судың сіңу жылдамдығының тығыздықтан тәуелді функциясын ескеріп, судың сіңу жылдамдығын деп алып , қорытындылай келе мына теңдікті аламыз:

.