14.Гамильтон—Якоби теңдеуі,мысал

Гамильтон—Якоби теңдеуін Гамильтон алғаш 1820 жылы толқындық және геометриялық оптика есебіне қолданған. 1834 жылы Гамильтон өз идеясын динамика есебіне қолданған.Ал, 1837 жылы К.Якоби бұл әдісті барлық классикалық вариациялық есептеулерге қолданды.

Теорема: Әрекет функциясы S(q,t)

( 1)

теңдеуін қанағаттандырады. Бұл бірінші ретті сызықты емес дербес туындылы дифференциалдық теңдеуін Гамильтон—Якоби теңдеуі деп атаймыз.

Дәлелдеуі:Теореманың дәлелдеуі үшін

теңдеуі жеткілікті. Механикалық жүйенің траекторияларының және дербес туындылы теңдеудің арасындағы байланысты екі бағытта қолдануға болады. Біріншіден, (1) теңдеуінің кейбір шешімін динамиканың жай дифференциалдық теңдеуін интегралдауға қолдануға болады. Екіншіден, сәулелі және толқынды байланыс көзқарасынан (1) дербес туындылы теңдеуін жай дифференциалды Гамильтон теңдеуінің интегралдық жүйесіне келтіруге болады. Бұл жайында толығырақ тоқталайық.Гамильтон-Якоби теңдеуіне (1), Коши есебін қояйық.

(2)

Бұл есептің шешімін табу үшін , Гамильтонның канондық теңдеулер жүйесін қарастырамыз.

1-сурет.Гамильтон-Якоби теңдеуі үшін қойылған Коши есебінің характеристикасы

Бастапқы шарттарын қарастырайық(1-сурет):

Бастапқы шарттарға сәйкес шешім (q,t)-кеңістігінде қисық q=q(t)

(Лагранжиан Лежандр түрлендіруі р бойынша Гамильтон функциясынан H(p,q,t)).Бұл экстремаль (2) есептің характеристикасы деп аталады, нүктесінен шыққан.

Егер мәні -дің мәніне жақын болса,жақын q нүктесінен шығатын характеристикасы,

кезінде тоғыспай ды. және t мәндерін А нүктесінің

,

облысындағы координаттары ретінде қарауға болады(1-сурет).

Енді « бастапқы шартымен әрекет функциясын» құрамыз:

(3)

Теорема: (3) функциясы (2) есебінің шешімі. Шынында да,бастапқы шарты айқын түрде орындалып тұрғаны көрініп тұр.Гамильтон—Якоби теңдеуінің орындалғандығы, әрекет функциясының дифференциалы туралы теоремадан тексеріледі(2-сурет).

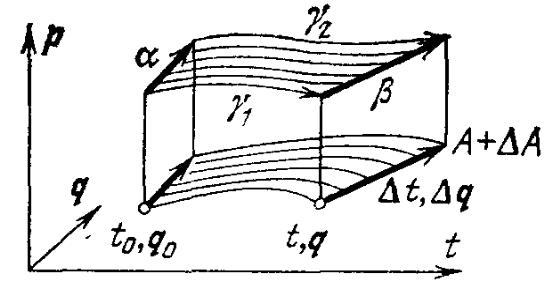2-сурет

Мысалы:

Есептің берілгені: Гамильтон функциясын эллиптикалық координатада анықтау.

Шешімі: =const сызығы, эллипс фокустары О1,О2, =const- гиперболалар сол фокустармен сызылған(3-сурет).Олар өзара ортогональді, өйткені а және b коэффициенттерін табайық.Эллипстың маңайындағы қозғалыстан шығады. Гиперболаның маңай-ындағы қозғалыстан екені шығады.Сонымен, Ары қарай, О1МО2 үшбұрышынан екенін табамыз, бұдан

Бірақ, егер

Сонымен,

Бірақ,

Соңында,

екені шығады.

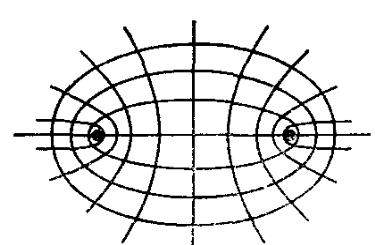3-сурет

15.Электромагнетизм заңдарына негізделген физикалық тәжірибелер

Электр зарядын қоршаған ортада электростатикалық өріс болатыны сияқты токтарды қоршаған ортада магнит өрісі болады. Магнит өрісі осы өріске әкелінген тоғы бар өткізгішке әсер ететін күш арқылы білінеді. Ток айналасында магнит өрісі болатынын бірінші рет 1820 жылы дат физигі Эрстед тәжірибе жүзінде ашқан. Ол тогы бар өткізгіш маңында магнит стрелкасын қойсақ, стрелканың ток бағытына қарай бұрылатынын байқаған. Магнит өрісін зерттеу үшін тогы бар жазық тұйықталған контур қолданылады. Рамка арқылы ток жүргенде, ол белгілі бір бұрышқа бұрылады. Рамканың айналу бағыты арқылы магнит өрісінің бағыты анықталады. Магнит өрісінің рамканы айналдырушы

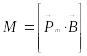(1.1)

мұндағы тогы бар рамканың магнит моменті векторы.

магнит индукция векторы, контурғы нормаль бірлік вектор, магнит өрісінің токқа әсер ететін күшін сипаттайды. Олай болса, магнит индукциясы айналу моментіне пропорционал шама

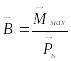(1.2)

Француз физиктері Био және Савар тәжірибелер арқылы әртүрлі пішінді тұрақты токтың айналасындағы магнит өрістерін зерттеген. Лаплас сол зерттеулердің нәтижелерін жинақтап кез келген пішіндегі контурдың бөліктеріне жарамды магнит өрісінің қорытқы индукциясын анықтауға болатын заңдылықты ашты.

Ол заңдылық бойынша J тогы бар өткізгіштің элементінің өрістің бір С

нүктесіндегі магнит индукциясы

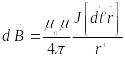модулы (1.3)

Осы өрнек, электромагниттік құбылыстар үшін Био-Савар- Лаплас заңы деп аталады.

векторы және құрайтын жазықтыққа перпендикуляр болып, индукция сызықтарына жанама болады, бағыты бұранда ережесі бойынша анықталады.

Суперпозиция принципін қолданып, барлық ток элементтерінің магнит индукциясы векторларының қосындыларын интегралдау арқылы анықтауға болады

. (1.4) Интегралды өткізгіштің ұзындығы бойынша аламыз. Био-Савар-Лаплас заңының кейбір симметриялы токтардың магнит өрісін есептеу үшін қолданылуы.

1. Шексіз түзу өткізгіштің бойымен өткен токтың магнит өрісін анықтау.

2. Дөңгелек токтың центріндегі магнит өрісін анықтау

Параллель токтардың. өзара әсерлесу күштерін анықтау үшін бір - бірінен d ара қашықтықта орналасқан шексіз ұзын, түзу параллель

өткізгіштерде J₁ және J₂ токтары болсын. Бұлардың әрқайсысы өз маңында магнит өрісін тудырады да олар Ампер заңы бойынша бір бірімен әсер етеді. J₁ тогы бар өткізгіштің магнит өрісіне J₂ тогы бар өткізгішті орналастырсақ, онда J₁ токтың магнит өрісінің күштері J₂ токтың d элементіне әсер етеді. Ампер заңына сәйкес J₁ ток тарапынан ал J₂ ток тарапынан күштері бір-біріне әсер етеді.

.

Олай болса, екі токтың арасындағы әсер күші

(1.5)

Бағыттас параллель токтар бір-біріне тартылады, қарама-қарсы токтар бір-бірінен тебіледі.

Электромагниттік индукция құбылысы. Бізге белгілі электр тогы өзінің айналасында магнит өрісін тудырады. Магнит өрісі мен электр тоғының арасындағы байланыс осы магнит өрісінің көмегімен контурда ток пайда бола ма деген сұрақтың шешімін 1831ж ағылшын физигі Фарадей шешті. Оның тәжірибесінде гальванометрге жалғанған катушканың (соленоид) ішіне, тұрақты магнит салсақ, гальванометр стрелкасының қозғалысын байқаймыз. Магнитті қайтадан суырып алсақ, стрелка басқа бағытқа ауытқиды. Магнитті неғұрлым тезірек қозғалтса, стрелка соғұрлым көбірек ауытқиды. Демек, магнит өрісінің күш сызықтары тұйық контурды қиып өткенде ток пайда болады, ол токты индукциялық ток деп атайды. Магниттің полюсін өзгертсек, стрелканың бұрылу бағыты өзгереді. Магнитті тұрақты қойып, соленоидты қозғауға да болады. Әрі осы пайда болған индукциялық ток, магнит ағынының өзгеру түріне байланыссыз, ол тек өзгеріс жылдамдығына байланысты. Магнит өрісі арқылы өндіріп алған индукциялық ток осы тізбекте ЭҚК бар екенін көрсетеді. Бұл ЭҚК электромагниттік индукцияның электр қозғаушы күші деп аталады. Яғни магнит өрісі арқылы индукциялық ток өндіріп алу құбылысын электромагниттік индукция құбылысы деп атайды.

Фарадей электромагниттік индукция заңын қорытып шығарды: өткізгіш контурында пайда болатын индукциялық ЭҚК шама жағынан сол контурмен шектелген бет арқылы өтетін магнит ағынының өзгеру жылдамдығына тура пропорционал да, бағыты жағынан оған қарама-қарсы (1.6)

Бұл электромагниттік индукция құбылысының негізгі заңы немесе Фарадей заңы деп аталады, әрі бұл универсиалды заң.

Мұндағы минус таңбасы магнит ағынының өзгерісінің өсуі , контурдағы ЭҚК азаюын туғызады, яғни индукциялық тоқтың өрісі магнит ағынына қарсы бағытталады; ал ағынның кемуі , ЭҚК туғызады, ағынының бағыты индукциялық тоқтың өріс бағытымен бағыттас болады. Бұл минус таңбасы орыс ғалымы Ленц ережесінің математикалық өрнегі. Ленц ережесі электромагниттік индукция нәтижесінде пайда болған индукциялық тоқтың бағытын анықтауға арналған негізгі ереже: тұйықталған контурда пайда болған индукциялық тоқтың бағыты, контур арқылы өтетін осы тоқты тудырған магнит ағынының өзгерісіне кедергі келтіре бағытталады.

Контурдың индуктивтілігі. Өздік индукция Қандайда бір тұйық контур арқылы ток жүрсе, оның магнит өрісі осы контур мен шектелген ауданды қиып өтеді. Контурдағы токтың шамасы өзгерсе, онда оның контуры арқылы өтетін магнит ағыны да өзгереді. Сондықтан контурда индукциялық ток пайда болады. Осындай контур арқылы жүретін ток өзгергенде, контурда индукциялық токтың пайда болуын өздік индукция құбылысы деп атайды. Ол электромагниттік индукцияның бір түрі. Катушкада ток өзгергенде оның магнит өрісі де өзгереді, демек катушканың өзінде ЭҚК пайда болады. Оны өздік индукциялық ЭҚК деп атайды. Био-Савар-Лаплас заңы бойынша екенін білеміз, олай болса магнит ағыны да тоққа тура пропорционал, яғни

(1.7)

Өзара индукция құбылысы. Бір-біріне жақын орналасқан екі қозғалмайтын тұйық контур қарастырамыз. Егер бірінші контурда ток жүрсе, онда осы ток тудырған магнит ағыны екінші контурды кесіп өтеді. Бұдан

(1.8)

мұндағы пропорционалдық коэффициент. Контурдағы ток өзгерсе, онда екінші контурда ЭҚК пайда болады. Фарадей заңы бойынша бұл ЭҚК 1-ші контурдағы тоқтан туған магнит ағынының өзгерісіне тең, бірақ бағыты жағынан қарама-қарсы:

.

Трансформаторлар. Бір кернеулі айнымалы тоқты екінші басқа кернеулі айнымалы токқа түрлендіретін электр техникалық құрал трансформаторлар деп аталады. Трасформатордың жұмыс істеу принципі өзара индукция құбылысына негізделген. Ең бірінші рет құрастырған орыс электр технигі физик П.Н.Яблочков. Трансформатор болаттан жасалған екі тұйық өзекшеден тұрады. Алғашқы орамы , орам саны айнымалы ток көзіне жалғанады. Оның міндеті өзіне келген айнымалы токты трансформатордың екінші орамына тасымалдау. Ал екінші орам өзіне келген айнымалы токты не күшейтеді, не әлсіретеді. Ол орам санына байланысты.

қубылыстарды ұзақ уақыт бойында зерттей келе Майкл Фарадей материя туралы корпускулалық теорияны континуальдық теориямен, яғни үздіксіздік теориясымен алмастыру керек деген ойға келді.Фарадей көзқарастарын жақтаушылардың бірі көрнекті ағылшын физигі және математигі Джеймс Максвелл болды. Оның электромагне-тизм теориясында электр мен магнетизмнің органикалық байланысы анықталды. Ертеректе Фарадей ашқан идеяларды негізге ала отырып, Максвелл электромагниттік өріс уғымын енгізді. Өзіне дейінгі тәжірибелік жолмен ашылған электромагниттік қубылыс заңдары мен М.Фарадей ашқан электромагнетизм индукциясы құбылысын біріктіріп, тужырымдап, Максвелл таза математикалық әдіспен электромагниттік өрісті өрнектейтін дифференциалды теңдеулер жүйесін тапты. Бул теңдеулер жүйесі электромагниттік қубылысты өз шамасында барынша толық өрнектейді және ньютондық механика жүйесі сияқты толық та жетілген жаңа теорияны сипаттайды. Осы теңдеулерден электрлік зарядтарға «байланбаған» өрістің жеке өмір сүру мумкіншілігі болуы керек деген маңыз-ды тужырымдама шығады.

Максвелл теориясы бойынша әрбір зарядталған үсақ бөлшек өріспен көрінбейтін жиекпен қоршалған, ол жақын маңайда орналасқан басқа зарядталған бөлшектерге әсер етеді, басқаша айтқанда, заряд-талған бір бөлшектің өрісі басқа бөлшектерге біршама кушпен әсер етеді. Әсер ету табиғатына мундай көзқарастар тартуды кеңістікпен бөлінген массалар арасындағы тікелей өзара әсер етудің күші деп есептейтін ньютондық тужырымдамадан айрықша ерекшеленеді. Максвелдің теориясында кеңістіктің берілген нүктесіне орналастырылған бөлшектің қозғалысы куштік сипатпен - осы нүктедегі кернеу күшімен анықталады.

Максвелдің электромагниттік өріс теориясы физика мен жараты-лыстануда жаңа кезеңнің басталуын анықтады деуге болады. Физика-ның дамуының дәл осы кезеңінде электромагниттік өріс өмір шындығына, өзара әсердің материалдық сақтаушысына айналды. Әлем бірте-бірте электрлі зарядталған бөлшектерден құрылған, электромагниттік өріс аркылы өзара әсерлесетін электродинамикалық жүйе болып ұғыныла бастады. Өз теңдеулерін талдай келе, Максвелл электромагниттік толқындар деп аталатын толқындар болуы керек деген қорытындыға келді және олардың таралу жылдамдығы жарықтың жылдамдығымен бірдей екендігін есептеп шығарды. Осыдан келіп жарық дегеніміз элек-тромагниттік толқындардың бір түрі деген қорытынды шығады.