10. Дивергенцияның физикалық мағынасы

Физика тұрғысынан қарағанда, векторлық өрістің дивергенциясы, берілген нүкте кеңістігі қандай деңгейде өріс ағынының қайнар көзі немесе тұтынушысы болатынының көрсеткіші. Яғни, дивергенцияның балама анықтамасы мына түрде:

Мұнда Ф – векторлық өріс F-тің ағыны, сфералық бет ауданы S арқылы V көлемімен шектелген. Бұл анықтама бірінші анықтамаға қарағанда, декарттық координат жүйесінен басқа да координат жүйелеріне қолданылады.

өріс нүктесі қайнар көзі болып табылады өріс нүктесі сток(ағып кету) болып табылады сток пен қайнар көз жоқ немесе олар бір-бірінің орнын толтырады

Мысалы, егер векторлық өрісті, жер бетіндегі ең жылдам түсу бағыттарының жиынтығы ретінде алсақ,онда дивергенция шыңдар мен ойыстарынының орналасуын көрсетеді, демек шыңдарында дивергенция оң болады(түсу бағыттары шыңдардан жинақталмайды), ал ойыстарда теріс(ойыстарға түсу бағыттары жинақталады).

Острогра́дский формуласы — векторлық өріс ағынын, тұйық бетін интеграл арқылы сол өрістің көлемінің дивергенциясы мен шектелген сол бетімен көрсететін математикалық формула:

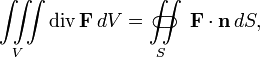
Яғни векторлық өріс дивергенциясынан интеграл, кей көлем арқылы таралған, тең болады бетімен осы көлемді шектейтін векторлық ағынға.

Формула көлемдік интегралды тұйықталған беттік интегралға өзгерту үшін қолданылады. Остроградский формуласы келесі түрде жазылған:

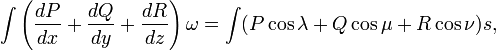
Мұнда және - көлем және бет бойынша дифференциалдар. Заманауи үлгіде - көлем элементі, - бет элементі. - тұйықталған облыс кеңістіктегі бірінші ретті дербес туындылы үзіліссіз функциялар.Жалпы түрдегі Остроградский формуласы Стокс формуласы болып табылады шек көпбейнелер үшін.

11.Ротордың физикалық мағынасы. Стокс теңдеуі.

Стокс теңдеуі. кеңістіктегі 2 өлшемді тегіс көпбейне болсын. көпбейне бетінің шекарасы және оның бағыты бағытымен келісілген.Енді 1-ші ретті сыртқы дифференциалдық тұрпатты жазайық:

=

мұндағы Аталған скалярдан вектор құраймыз:

векторына тұрпаты сәйкес келеді. Олай болса бұл бірмәнді сәйкестік.

Егер тұрпатты дифференциалдар болсақ

аламыз.

Ұқсас дифференциалдардың көбейтіндісі 0-ге тең екенін ескере отырып жақшаны ашамыз:

Соңғы пайда болған өрнек векторының роторына пара-пар

rot = ,

яғни,

сыртқы дифференциалдау амалы роторға сәйкес келеді.Олай болса Стокс теңдеуі

мына түрде жазылады және кеңістіктегі Стокс фрмуласы деп аталады.

Ротордың физикалық мағынасы. Ротор дегеніміз өрістің құйындылығын анықтайтын характеристика болып табылады. 1 нүктедегі құйындылықты көрсету үшін 3 жазықтықта жататын контурдың циркуляциясын қарастырамыз. Осыдан шығатыны :

Осыдан шығатын ротор орта қозғалысының айналушы бөлігін толықтай қарастырады.

12.Электромагнетизм заңдары

Электромагнетизмнің 4 заңы бар.

Электромагнетизмнің 1-ші заңы. ағыны тұйық беттен өтетін зарядтардың қосындысына тең.

Егер бет ішінде заряд болмаса, онда -ге тең болады.Зарядтың орналасуын анықтаймыз.

ллв

Мұндағы - кернеуліктің тұйық бет бойынша ағыны, q- ішкі заряд, ал V- көлем.

Электромагнетизмнің II-заңы.Тұйық беттен магнит ағынының өзгеру жылдамдығы электр өріс -кернеуліктің циркуляциясын береді. Магнит ағыны өзгермесе циркуляция нөлге тең. Яғни

ағыны

М

Магниттік өрістің өзгерісінен циркуляция немесе ток пайда болады.

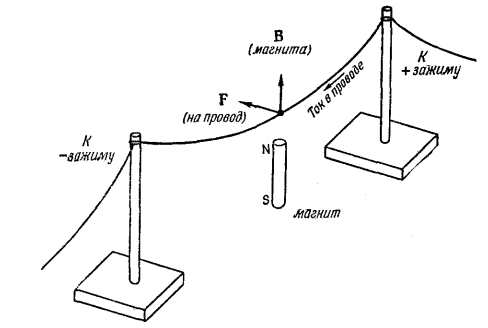
Ток қосылған уақытта күш әсерінен сым қозғалады. Бұны мына теңдеумен өрнектеуге болады:

Электромагнетизмнің III-заңы. Тұйық заттың шекарасы жоқ.В ағыны тұйық бет арқылы магниттік заряд жоқ ,сондықтан нөлге тең.

ағыны

Электромагнетизмнің IV-заңы. Магниттік өрістің циркуляциясы С контур бойынша циркуляциясына тең болады.

ағыны

Мұндағы М –электр тогы.