6.Екінші ретті сыртқы дифференциалдық тұрпаттар.

Екі өлшемді тегіс көпбейне берілсін. Оны М деп белгілеп R ⁿ кеңістігінде қарастырайық. 21- суретте М көпбейненің х нүктесінде ТМ_х жанама жазықтығы көрсетілген.

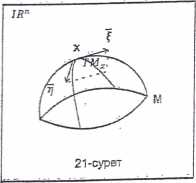
Қос жанама векторлар алайық, яғни , ТМ_х. Екі вектор параллеграмм құрайды. Параллелограммды ох¹х² жазықтығына проекциялайық. (22 сурет)

22 Сурет

Олай болса, проекцияның ауданы келесі анықтауыштың мәніне тең.

мұндағы = , =

Бұл анықтауышты ( , ) деп белгілейміз, яғни

( , ) =

Сонымен ( , ) екі жанама вектордан = , = құралған параллелограммның ох¹х² жазықтыққа проекциясының ауданына тең. Проекцияның ауданының қасиеттерін айта кетейік:

1. ( + , ) = ( , ) + ( , )

2. ( , ) = – ( , )

Басқаша айтқанда, проекция ауданы аймағынан сызықтық функция және параллелограммның қабырғаларын орын ауыстырса, онда ауданның таңбасы қарама – қарсығы ауысады. Бұл қасиеттерді анықтауыштардың қасиеттерінен де байқауға болады.

= +

–

R ⁿ кеңістігінде екі жанама ветордың , құралған параллелограммды басқа жазықтықтарға проекциялауға болады. Мысалы,

( , ) =

ох¹х³ жазықтыққа проекцияланғанда шығатын аудан.

Дәл сол сияқты келесі проекциялардың аудандарын

….. …… .. …..

Проекциялардың қарастыруға болады. Жалпы аудандардың сызықты тіркесі келесі түрде

Жазылады және екінші ретті сыртқы дифференциалдық тұрпат деп аталады. Сонымен екінші ретті тұрпаттың жалпы түрі:

( , ) = ( , ) + …..+ ( , ),

мұндағы: М , , ТМ_х cкаляр функциялар.

Жаттығу 3. Келесі тепе-теңдік = орынды.

Дәлелдеуі. ( , ) = өрнегін қарастырайық.

Дәл сол сияқты ( , ) =

Соңғы екі теңдікті салыстыру арқылы қажетті тепе-теңдікке көзіміз жетеді.

Бірінші ретті дифференциалдық тұрпаттардың жалпы түрі.

Алдымен қисықсызықты интегралды қарастырайық.

Мұндағы с-бірлік шеңбер болсын. Бұл интегралды анықталған интегралға келтіруге болады.

= =

Сонгы теңдікті келесі түрде жазуға болады:

= (*)

Егер деп алсақ.

(*) Теңдіктің сол жағына қарастырсақ, онда

– интегралданатын функция,

– элементар ұзындық,

- интервал деп аталады. Енді (*) теңдіктің оң жағына назар аударайық. – ( ) интервалының үзіліссіз өзгеруі деп ойлауға болады, демек - бір өлшемді тегіс көпбейне.

Бұдан шығатын қорытынды математикалық анализдегі интегралданатын функция, элементар ұзыңдық деген ұғымдар қолайсыз, себебі интервалдан көпбейнеге көшкен кезде талаған ұғымдар жойылады. Сондықтан тиімді жаңа тілге көшу қажет. Ол үшін деген өрнекті тұтас қарастырайық, сонда 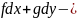тұтас болады.

Сонымен және деген өрнектер ыңғайлы екенін болашақта көрсетеміз. Бұндай өрнектер сыртқы дифференциалдық тұрпаттар деп аталады. Дәл сол сияқты

деген өрнектерде сыртқы дифференциалдық тұрпаттар деген дұрыс болады. Алдыңғы тұрпаттарды кейінгі тұрпаттардан ажырату үшін тұрпаттың реті деген ұғым енгіземіз. Сонымен және бірінші ретті сыртқы дифференциалдық тұрпаттар, ал

екінші ретті сыртқы дифференциалдық тұрпаттар деп айтамыз.