4.2 Өлшемді көпбейнеге арналған жанама кеңістік, мысал: Бірлік сферадағы жанама кеңістік. Нормаль арқылы сфераның бағыты.

Қисықтардың, беттердің және к-өлшемді көпбейнелердің кесінділермен, жазық пішіндермен салыстырғанда бір өзгешелігі бар. Қисықтың жанамасы қисықпен беттеспейді. Сол сияқты беттің жанама жазықтығы бетпен беттеспейді. Жалпы жағдайда к-өлшемді тегіс көпбейнемен беттеспегендікпен, оларды жеке қарастыру қажет. 16-суретте кейбір көпбейнелердің жанама кеңістіктері көрсетілген. Көпбейненің әр нүктесіне жеке жанама кеңістік тиісті. Басқаша айтқанда, көпбейне – ол нүктелердің жиыны, ал әр нүктеде оған сәйкес жанама кеңістігі бар. Сондықтан әдетте көпбейнені

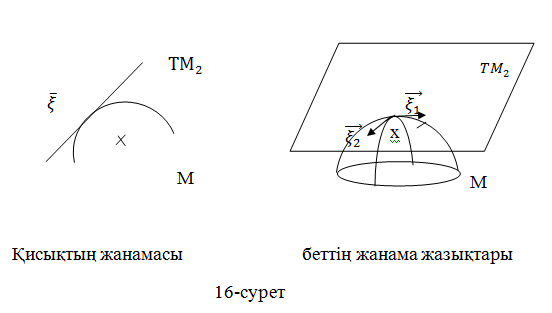
және оған сәйкес жанама кеңістіктерін бірге қарастырған жөн. Сонымен көпбейненің әр нүктесінде жанама векторлардан құрастырылған реперлерді қарастыру қажет.

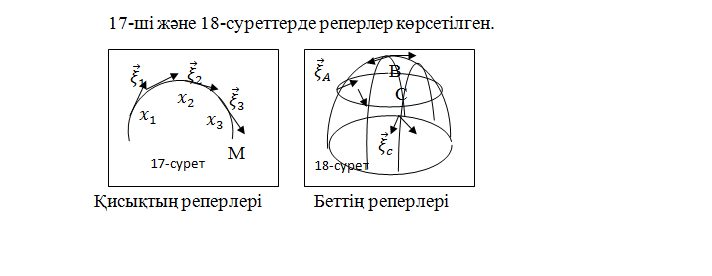
Мысал:

,

Мұндағы

0< ,

Егер болса, онда x,y,z келесі түрде болады

Мұннан

Егер , болса онда

Мұннан

Нормаль анықтама бойынша келесі теңдеуді қанағаттандырады.

|| ||=1

Әр нүктеде нормаль сыртқа бағытталған. Жанама нормальға .

5.1-ретті сыртқы дифференциалдық тұрпаттар. Бірінші ретті тұрпаттардың жалпы түрі. Геометриялық мағынасы.

к-өлшемді тегіс көпбейнелердің бойында к-ретті сыртқы дифференциалдық тұрпаттарды анықтауға дайынбыз. к=1 болған жағдайдан бастайық.

Бір өлшемді тегіс көпбейне берілсін. (19-сурет).

x

М

19-сурет

Көпбейненің кез келген x нүктесінде Т жанамасын қарастырайық. Жанама векторды -деп белгілеп алайық.

20-суретте жанама векторы көрсетілген және оның , остеріне проекциялары сызылған. Проекциялардың ұзындықтары алгебрада деп белгілейді. Олай болса, келесі сызықты бейнелеуді қарастыруға болады:

x

0

y

20-сурет

яғни жанама векторға оның осіне түскен проекцияның ұзындығын сәйкес қоямыз. Математикалық анализде векторының проекциясының ұзындығы деп белгіленеді.

Сондықтан әдетте аталған бейнелеуді келесі турде

жазады. Дәл сол сияқты екінші бейнелеу

проекция алу амалы пайда болады. Сызықты амал, сондықтан олардың сызықты тіркесі де сызықты болады. Проекциялардың сызықты тіркестерін сызықты дифференциалдық тұрпаттар деп атайды. Сонымен бірінші ретті сыртқы дифференциалдық тұрпаттың жалпы түрі келесі

W = 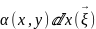+ (x,y) ,

мұндағы -скаляр функциялар. Егер x= ) болса, онда -дегі бірінші ретті сыртқы дифференциалдық тұрпаттардың жалпы түрі келесі

W = + …. + , x M, Т

мұндағы , ..., -скаляр функциялар.

Жаттығу 1. -дегі бірінші ретті сыртқы дифференциалдық тұрпаттар жиыны сызықты кеңістік құрайды және оның өлшемі n-ге тең.

Шешуі. Дифференциалдық тұрпаттарды өзара қосуға болады. Еселеуге де болады. Сондықтан олардың жиыны сызықты кеңістік ретінде қарастыруға болады. Аталған сызықты кеңістіктің базисі ретінде , , ..., алуға болады, демек өлшемі n-ге тең.