С) Мына түрдегі тұрпаттарды ықшамдаңыз:
Берілгені:
Шешуі:
(ξ
, η
) екі жанама вектордан
ξ=(
,
,…,
),
,
,…,
)
құралған параллеограммның жазықтыққа проекциясының ауданына
тең. Проекцияның ауданының қасиеттерінің бірі:
(ξ , η ) = - (η, ξ )
және индекстердің ішінде кемінде екеуі өзара тең болса, онда
d ^…^
анықтамаларын пайдалана отырып
,
,
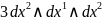=0
екендігін
анықтаймыз. Сәйкесінше есебіміздің
шешуі
болады.
Жауабы:
=
.
D) Жақшаларды ашыңыз және ықшамдаңыз:
Берілгені:
Шешуі:
(ξ , η ) екі жанама вектордан
ξ=( , ,…, ), , ,…, )
құралған параллеограммның жазықтыққа проекциясының ауданына
тең. Проекцияның ауданының қасиеттерінің бірі:
(ξ , η ) = - (η, ξ )
және индекстерінің ішінде кемінде екеуі өзара тең болса,
d ^…^
анықтамаларын пайдалана отырып, келесі есептеулерді жүргіземіз:
Жақшаларды ашып аламыз:
=
=
;
Сәйкесінше есебіміздің шешуі
.
Жауабы:
E)
df ∧
dg формасын, мұндағы f=ln(1+
);
g= sin|x|; x=(
)
мындағы түрдегі комбинация тұрпатында
жазыңыз
, 1
Шешуі: Есепті шығару үшін мына анықтамаларды пайдаланамыз:
(ξ , η ) екі жанама вектордан
ξ=( , ,…, ), , ,…, )
құралған параллеограммның жазықтыққа проекциясының ауданына
теңдігінен шығатын қасиеттерінің бірі:
(ξ , η ) = - (η, ξ ) (1)
Индекстерінің ішінде кемінде екеуі өзара тең болса,
d ^…^ , (2)
және толық дифференциал анықтау формуласын:
df=
(3)
df ∧ dg формасын анықтау үшін алдымен df және dg-ді табамыз. Олар (3) формула бойынша
df=
,dg=
табылады. Яғни,
f=ln(1+
);
g= sin|x|; x=(
)
df=
+
, dg= cos |x|
.
=(
+
^
( cos |x|
),
жақшаларды ашсақ
+
^
+
+ теңдігі шығады. Осыдан (1) және (2)
формулаларды пайдалану нәтижесінде:
-
+
=0
теңдіктің нөлге тең екенін анықтаймыз.
Жауабы: df ∧ dg=0.