50.Есептің берілгені :

Шешуі:

x және t – айнымалыларына тәуелді квазисызықты Хопф теңдеуі. Жалпы бұл теңдеу мына формуламен анықталады:

формуланы ашып жазсақ:

Коши шартын: қарастырамыз.

Есептің берілгені бойынша мына түрдегі Хопф теңдеуін құрамыз:

Құрылған Хопф теңдеуіне байланысты Гамильтон-Якоби теңдеуінен құрылған характеристикалық жүйені қарастырамыз:

Осы формула арқылы орнына қоямыз,

Есептің берілгеніндегі бастапқы шартты қанағаттандыратындай етіп характеристикалық жүйені шешеміз:

Демек, ізделінді функция осы теңдікті қанағаттандырады:

51.Есептің берілгені :

Шешуі:

Берілген есебімізде t және x – айнымалыларына тәуелді квазисызықты Хопф теңдеуін қарастырамыз. Жалпы бұл теңдеу мына формуламен анықталады:

бұл формуланы ашып жазсақ:

Коши шарты мынаған тең:

Яғни осыдан:

Бұл есептен келесі характеристикалық жүйеге көшеміз.

Осы формула арқылы орнына қоямыз.

Жауабы:

52.Есептің берілгені:

а)Rⁿ кеңістігінде тексеріңіз:

df¹^...^dfⁿ(x)=det (dfⁱ/dx^j)(x)dx¹^...^dxⁿ

Бұл жағдайды тексеру үшін n=3 болғандағы жағдайды қарастырайық:

Осы мысал арқылы а) жағдайының орындалғанын көріп тұрмыз. а) жағдайы дәлелденді.

Есептің берілгені:

в) Барлық есептеулерді жүргізіп, болғанда көрсетіңіз:

Бұл жағдайда к=2 болғандағыны көрсетейік:

Бұдан шығатын қорытынды, в) жағдайы айқын түрде дәлелденіп тұр.

53.Есеп. Төменде көрсетілген дифференциалдық тұрпатттарды ω тиісті – ғы векторлар жиынтығында мәндерін анықта :

a) ω = d ξ =(1,2,3) € T векторында

b) ω = d ˄ d + d ˄ d € T реттелген векторлар жұбында

c) ω = df , мұндағы f = +2 a € T

Есептің шешімі:

a) ω = d ξ =(1,2,3) € T векторында

Бізге белгілі d ( ξ ) = 1 ,ал x координаталары ( 3,2,1) тең, мұндағы ал = ( 1,2,3) ке тең. Орнына қойып ω –ны есептесек ω = 2*1=2.

b) ω = d ˄ d + d ˄ d € T реттелген векторлар жұбында мәнін табатын болсақ,онда төмендегі жолмен анықталады.

ω ( , 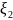) = d ˄ d ( , ) +1*d ˄ d = ( - ) + ( - )

c) ω = df , мұндағы f = +2 a € T

есептің шешімі келесі түрде болады:

ω ( ) = ( d ) ( ) = 1 – 2 + 3 - *n = ¼

себебі, s= 1 – 2 +3 -4 + 5… деп алсақ , онда төмендегі есептеу нәтижесінде табылады.

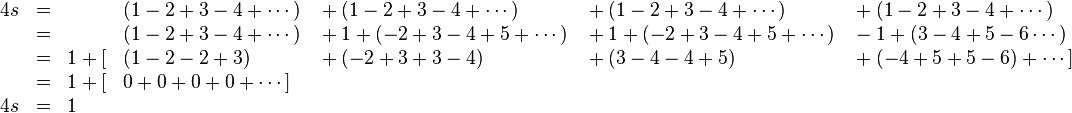
Бұл жерден s – тің мәні ¼ ке тең.

54.А) d ^…^ тұрпаттың 0-ге тең екенін көрсетіңіз, егер барлық индекстердің ,…, араларында өзара теңдері болса:

Индекстердің ішінде кемінде екеуі өзара тең болса, онда

d ^…^ ,

себебі d ^…^

d (ξ) … d (ξ)

d ^…^ ( ξ ,…. ,η )=

d (η) … d (η)

түрінде анықталады. Яғни, индекстері тең болса анықтауыштың сәйкес бағандары тең болады. Олай болса d ^…^ теңдігі орынды.

В) Неге n-өлшемді векторлық кеңістікте нөлден өзге коссосимметриялық p>n дәрежелі тұрпаттар жоқ екенін түсіндіріңіз

Себебі, р дәрежелі тұрпат сәйкесінше

формуласымен анықталады, яғни n<p болғандықтан бұл тұрпаттың ішінде

x=( ,…, ) бар деген сөз. Индекстердің ішінде кемінде екеуі өзара тең болса, онда d ^…^ болғандықтан, n-өлшемді векторлық кеңістікте нөлден өзге коссосимметриялық p>n дәрежелі тұрпаттар болмайды.