Maple программасында есептің шешімінің графигін тұрғызайық:
>
>
>
>
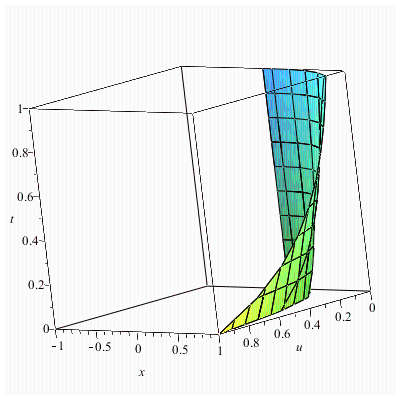
32.Хопф теңдеуі үшін t>0 мезетіндегі жылдамдығының үлестірілуінің графигін тұрғызу, егер
Бізге Хопф теңдеуінің түрі: мынандай екені белгілі ,ал есеп бойынша бастапқы шарт мұндағы Өзіміз және үшін мынандай алмастырулар енгіземіз:
Бұдан f мынаған тең: f=p*u ; q=-f; =u; =p;
=u; бұдан ;бұдан x=u*t+x(0);
x(0)= ;u= ;
x=u*t+x(0); бұдан x= *t+ ; =
Бастапқы
шарт
болғандықтан,
бұдан
Бұл
есептің шешімі:
Тексеру:
=-
;
=-
;
+
*
=0;
Maple программасында есептің шешімінің графигін тұрғызайық:
>
>
>
>
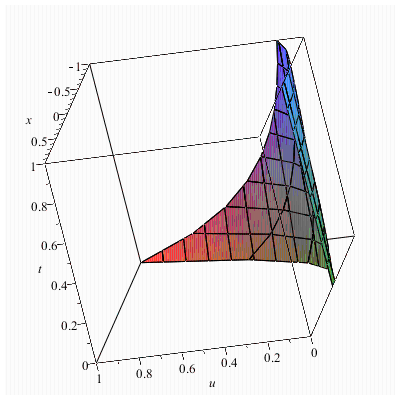
33.Кoши есебінің максималды Т>0 табыңыз
,
Бұл есептен келесі характеристикалық жүйеге көшеміз:
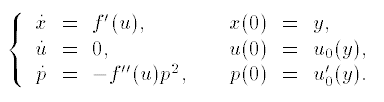
(1)
Бұл жүйенің шешімі келесі түрде өрнектеледі:
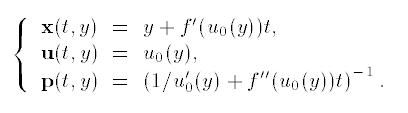
(2)
Есептің берілгені бойынша:
Ал екінші ретті туындысы төмендегіше болады:
(2)
жүйенің 1-ші теңдеуінен =>
(2)
жүйенің 2-ші теңдеуінен =>
(2) жүйенің 3-ші теңдеуінен =>
екендігінен=>
(2) жүйенің 2-ші теңдеуінен=>
шығатыны анық.
Демек,
.
Олай болса:
екендігі шығады.
34.Кoши есебінің максималды T>0 табыңыз
,
Бұл есептен келесі характеристикалық жүйеге көшеміз:
(1)
Бұл жүйенің шешімі келесі түрде өрнектеледі:
(2)
Есептің берілгені бойынша:
Ал екінші ретті туындысы төмендегіше болады:
(2) жүйенің 1-ші теңдеуінен =>
(2)
жүйенің 2-ші теңдеуінен =>
(2) жүйенің 3-ші теңдеуінен =>
екендігінен=>
(2) жүйенің 2-ші теңдеуінен=>
шығатыны анық.
Демек,
.
Олай болса:
екендігі шығады.
Осы теңдеуді maple-да салу арқылы Кoши есебінің максималды Т>0 табамыз.
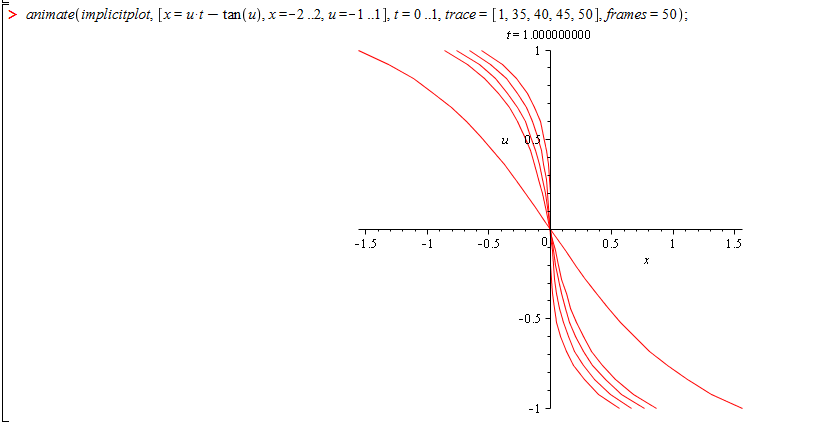
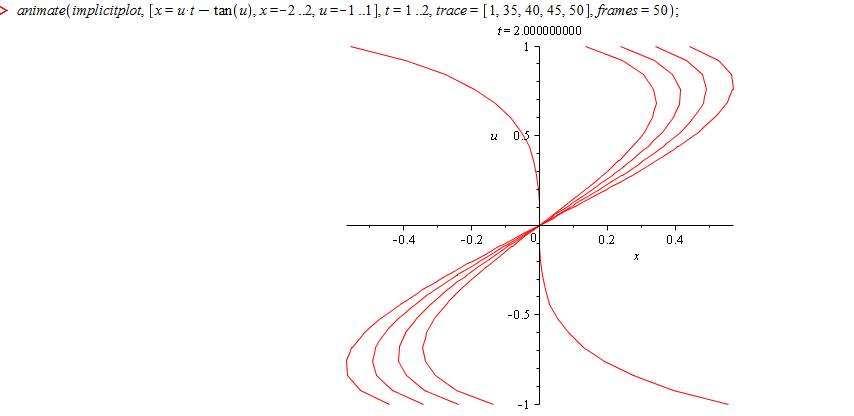
Бұл графиктерден Кoши есебінің максималды T>0 уақытын көруге болады. Бірінші графикте, T=0..1 аралығында функция бір мәнді табылады,яғни бір х-ке бір у сәйкес келеді, ал екінші графикте T=1..2 аралығында функция бір мәнді табылмайды, оны графиктен анық байқауға болады. Демек, максималды T=1 екенін табамыз.
35.Кoши есебінің максималды Т>0 табыңыз
,
Бұл есептен келесі характеристикалық жүйеге көшеміз:
(1)
Бұл жүйенің шешімі келесі түрде өрнектеледі:
(2)
Есептің берілгені бойынша:
Ал екінші ретті туындысы төмендегіше болады:
(2) жүйенің 1-ші теңдеуінен =>
(2)
жүйенің 2-ші теңдеуінен =>
(2) жүйенің 3-ші теңдеуінен =>
екендігінен=>
(2) жүйенің 2-ші теңдеуінен=>
шығатыны анық.
Демек,
.
Олай болса:
екендігі шығады.
Осы теңдеуді maple-да салу арқылы Кoши есебінің максималды Т>0 табамыз.
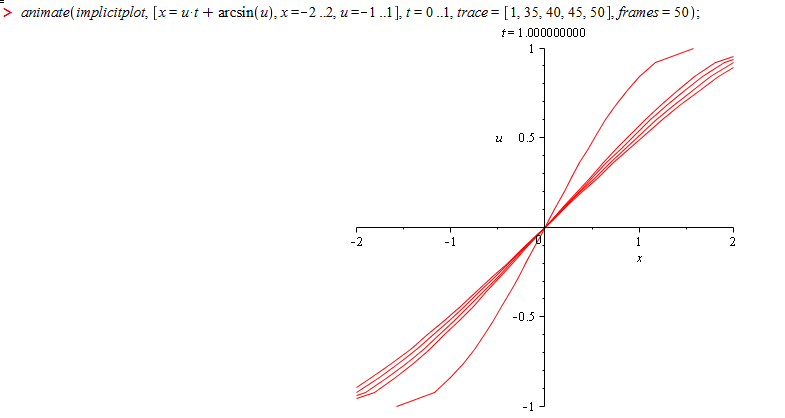
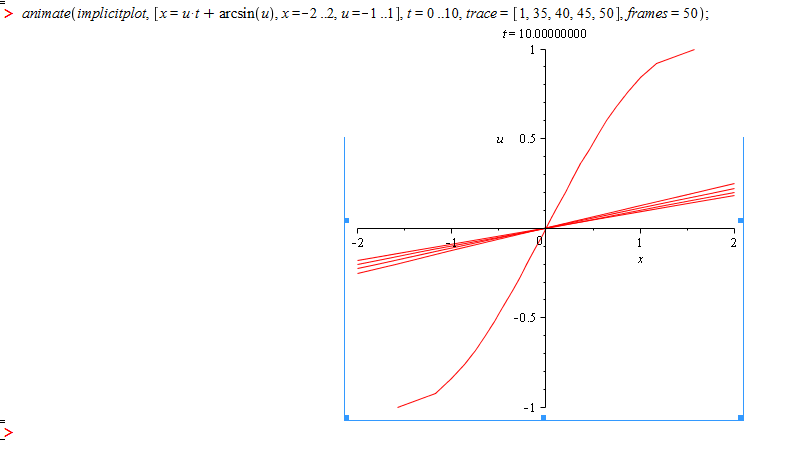
Бұл графиктерден Кoши есебінің максималды T>0 уақытын көруге болады. Бірінші графикте, T=0..1 аралығында функция бір мәнді табылады,яғни бір х-ке бір у сәйкес келеді, ал екінші графикте T=0..10 аралығында да функция бір мәнді табылады, оны графиктен анық байқауға болады. Осылайша, T-нің кез келген мәнін қойып қарасақ, функция бір мәнді табылады.
Демек, T-ның кез келген мәнінде Коши есебінің шешімі бар екенін көреміз.
36.Кoши есебінің максималды Т>0 табыңыз
,
Бұл есептен келесі характеристикалық жүйеге көшеміз:
(1)
Бұл жүйенің шешімі келесі түрде өрнектеледі:
(2)
Есептің берілгені бойынша:
Ал екінші ретті туындысы төмендегіше болады:
(2) жүйенің 1-ші теңдеуінен =>
(2)
жүйенің 2-ші теңдеуінен =>
(2) жүйенің 3-ші теңдеуінен =>
екендігінен=>
(2) жүйенің 2-ші теңдеуінен=>
шығатыны анық.
Демек,
.
Олай болса:
екендігі шығады.