22.Бірінші ретті дербес туындылы сызықты емес теңдеу үшін Коши есебінің шешімі
Бірінші ретті дербес туындылы теңдеу ұғымы туындыдан кейін пайда болған, яғни XVIII ғасырда қалыптасқан. Бұл теңдеулерді жай дифференциалдық теңдеулер сияқты шешу үшін,оған сәйкес характеристикалық жүйе құрамыз. Сызықты емес бірінші ретті теңдеу келесі түрге ие :
(1)
Егер (1) теңдеудің шешіміu(x) болса,онда функциясы квазисызықты емес теңдеуді қанағаттандырады. Біз функциясын екі рет үзіліссіз дифференциалдасақ (1) теңдеудің u(x) шешімі мына түрге келеді:
.
теңдеуін бойынша дифференциалдасақ
-ға қатысты квазисызықты теңдеу аламыз
Бұл теңдеу үшін характеристикалық жүйе келесі түрге ие:
Әрбір үшін алынған характеристикалық теңдеулерді біріктірсек келесі теңдеулер алынады:
,
Енді u-ға қатысты теңдеуді алу керек ол үшін u(x) функциясынан жүйесіне қатысты туынды аламыз:
Сонымен , 2n+1 теңдеуі үшін алынған
(4)
Жүйесі (1) cызықты емес теңдеу үшін характеристикалық жүйе болып табылады.
Мысалы,
бірінші ретті дербес туындылы сызықты
емес теңдеу үшін Эйконал теңдеуі үшін
Коши есебін шешіңіз
Шешуі:
Бірінші
ретті дербес туындылы теңдеу мен Коши
шарты берілген:
Сәйкесінше, х-тің үш компоненті болады:
U-дің х бойынша туындысының да үш компоненті төмендегідей болады:
=>
=>
шығатыны
анық.
деп
белгілеулер енгізейік.Олай болса,
,
,онда
Берілген
функциясынан
бойынша туындыларын табамыз:
, 
,
, 
Олай болса,(4) –ші характеристикалық жүйеден, келесі жүйені аламыз:
Жазықтық
бойындағы U-дің мәндері нөлге тең:
p-
вектордың ұзындығы бірге тең, яғни
.Олай
болса, р- бірлік вектор:
Кез
келген
,
,
орынды.
2t+
=0
=-
+
U(x)
=
Жауабы: U(x) =
23.Эйконал теңдеуі үшін Коши есебін шешіңіз
Шешуі:
Бірінші
ретті дербес туындылы теңдеу мен Коши
шарты берілген:
,
, , ,
Жазықтық бойындағы U-дің мәндері нөлге тең:
Р- вектордың ұзындығы бірге тең, яғни р- бірлік вектор:
Кез келген , , орынды.
2t+ =0
=- +
U(x) =
Жауабы: U(x) =
24.Эйконал теңдеуі үшін Коши есебін шешіңіз
Шешуі:
Бірінші ретті дербес туындылы теңдеу мен Коши шарты берілген:
(t,
, pt+x(0)=
, 
=const,
алғашқы
шарт p=
,
u(x,t)
X(0)=
U(
P= =>P(0)=
x=
;
U(x,t)=(
Тексеру:
t=0
=>
Жауабы:
29.Хопф
теңдеуі үшін t>0 мезетіндегі
жылдамдығының үлестірілуінің графигін
тұрғызу егер,
Хопф
теңдеуінің түрі:
,
мұндағы
f=p*u ; q=-f;
=u;
=p;
=u;
Соңғы
теңдік мына түрге ие
,бұл
теңдікті интегралдасақ x=u*t+x(0)теңдігін
аламыз;
x(0)= ;u= белгілеуін енгіземіз
Сонда
x=u*t+x(0) теңдігі
мына түрге ие болады
x=
*t+
;
=
Бастапқы
шарт
Тексеру:
=
;
=
;теңдіктерін
сәйкесінше
Хопф теңдеуіне әкеліп қоямыз.
Сонда
+(
=0теңдігі
шығады.
Maple программасында есептің шешімінің графигін тұрғызайық:
>
>
>
>
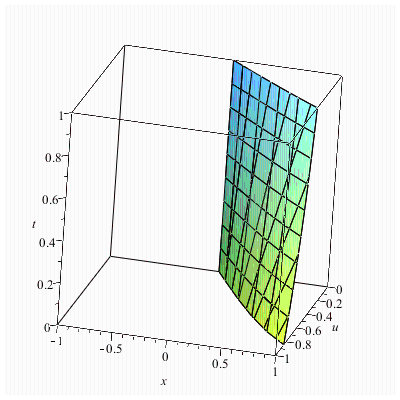
30.Хопф
теңдеуі үшін t>0 мезетіндегі 
жылдамдығының үлестірілуінің графигін
тұрғызу, егер
Бізге
Хопф теңдеуінің түрі мына түрде екені
белгілі: 
. Ал есеп бойынша бастапқы шарт
мұндағы
Өзіміз
және
үшін мына түрде алмастырулар енгіземіз:
Бұдан f мынаған тең:
f=p*u ;
q=-f;
=u;
=p;
=u;
бұдан ;
бұдан x=u*t+x(0);
x(0)-ді мына түрде аламыз:
x= *t+ ;
=
Бастапқы
шарт
Тексеру:
=
;
=
;
теңдіктерін
сәйкесінше
Хопф теңдеуіне әкеліп қоямыз.
Сонда -( =0 теңдігі шығады.
maple
программасында есептің
шешімінің графигін тұрғызуы:
>
>
>
>
>
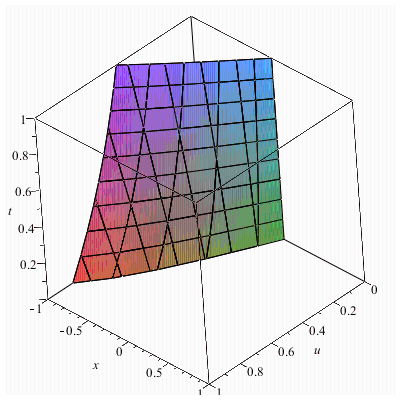
31.Хопф
теңдеуі үшін t>0 мезетіндегі
жылдамдығының үлестірілуінің графигін
тұрғызу, егер
Бізге
Хопф теңдеуінің түрі:
мынандай екені белгілі ,ал есеп бойынша
бастапқы шарт
мұндағы
Өзіміз
және
үшін мынандай алмастырулар енгіземіз:
Бұдан f мынаған тең: f=p*u ; q=-f; =u; =p;
=u; бұдан ;бұдан x=u*t+x(0);
x(0)= ;u= ;
x=u*t+x(0); бұдан x= *t+ ; =
Бастапқы
шарт
болғандықтан,
бұдан
Бұл
есептің шешімі:
Тексеру:
=
;
=
;
-
*
=0;