1. Карта. Атлас. Бағыт. 1 өлшемді көпбейне. Мысал: Шеңбер- 1 өлшемді көпбейне

–жазықтығында (а,b) интервалы берілсін.(1-сурет).

I

a b

1-сурет

(а,b) интервалының кеңістігінде үзіліссіз өзгеруін қарастырайық .(2-сурет).

I Интервалдың өзгерген бейнесін

кеңістіктегі қисық деп атайды. 2-суретте

өзгерген бейнесі бұранды сызық ретінде

көрсетілген. Бағытталған интервалдың

үзіліссіз бейнесі- бағытталған қисық.

кеңістігінде ( ; ; ) координатталар

жүйесін қарастырайық. Олай болса қисықтың әр нүктесі ( ; ; ) бір t-ға сәйкес келеді. Басқаша айтқанда, қисықтың картасы келесі түрде жазылады:

a< t< b

Мұндағы көпбейне t ( ; ; ) бір мәнді дифференцианалданатын сәйкестік. Сондықтан кеңістіктегі қисықты бір өлшемді тегіс көпбейне деп атайды. Алдындағы мысалымызда бір өлшемді тегіс көпбейненің атласы бір картадан тұрады ,яғни ол - бір карталы бір өлшемді тегіс көпбейне. Жалпы жағдайда бір өлшемді тегіс көпбейне бірнеше картадан тұруы мүмкін. Онда әр бөліктің жеке картасы болады. Ал атлас- барлық карталардың жиынтығы.

Бірнеше карталы атласқа мысал ретінде шеңберді алайық. Келесі суретте шеңбердің екі картасы көрсетілген. Бірінші картасы АSB доғасына арналған:

S I

C D

A NNN B

N

3-сурет

4-суретте АSB доғасы (а,b) интервалының өзгеруі екені көрсетілген.

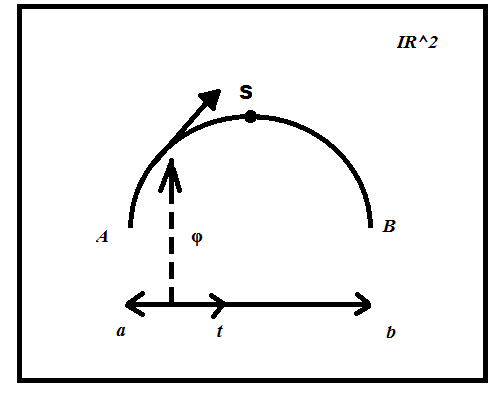
4-сурет

5-суретте екінші картаға сәйкес, демек CND доғасы (c,d) интервалының өзгеруі екенін байқауға болады.

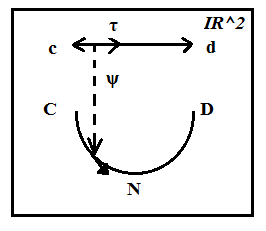
5-сурет

Сонымен шеңбердің атласы екі картадан тұрады. Бірінші карта келесі функциялар арқылы жазылады:

a< t< b

Ал екінші карта басқа екі функция арқылы өрнектеледі:

c< τ< d.

Айталық, n≥2 болсын. Жалпы жағдайда кеңістігінде бірөлшемді көпбейненің картасы келесі түрде жазылады:

: = ,…, = (t), a<t<b;

Бұл карта М көпбейненің бір бөлігіне ғана арналған , демек . М көпбейненің атласы бірнеше карталардан тұрады, демек атлас ={ } және .

Тұжырым 1. Шеңбердің атласы кемінде екі картадан тұрады.

Атластың мысалы ретінде Азияда орналасқан мемлекеттердің карталарын қарастырырайық. Оның ішініен Қазақстан және Өзбекстан карталарына тоқталайық. Осы екі карталарда Шымкент және Ташкент қалаларының бар екенін байқауға болады. Егер Қазақстан картасында Шымкенттен Ташкентке бару бағыты солтүстіктен оңтүстікке болса, онда Өзбекстан картасында Шымкенттен Ташкентке бару жолы бағыттас болуы қажет. Карталар бағыттастығына мысал ретінде 4-ші және 5-суреттердегі карталарды алсақ болады. 4-ші және 5-суреттердегі карталар өзара бағыттас бола ма деген сұраққа жауап беріп көрейік: карталар бағыттас емес, себебі 4–карта сағат тілімен бағыттас, ал 5-карта – сағат тіліне қарама-қарсы бағытта.Ал олар бағыттас болу үшін не істей аламыз? Ол үшін параметрдің бағытын қарама-қарсы бағытқа өзгерту қажет, демек праметрі -дан с-ға дейін жүру қажет.

6-суретте қажетті өзгерістер көрсетілген:

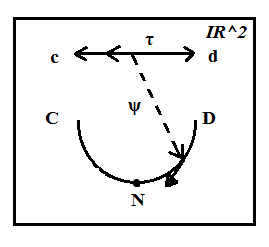
6- сурет

Қорытынды: Бір өлшемді тегіс көпбейнелер өзара бағыттары келісілген карталар арқылы беріледі. Карталардың жиыны атлас деп аталады. Әр карта интервалдың үзіліссіз өзгеру бейнесі болады.