Билет 13

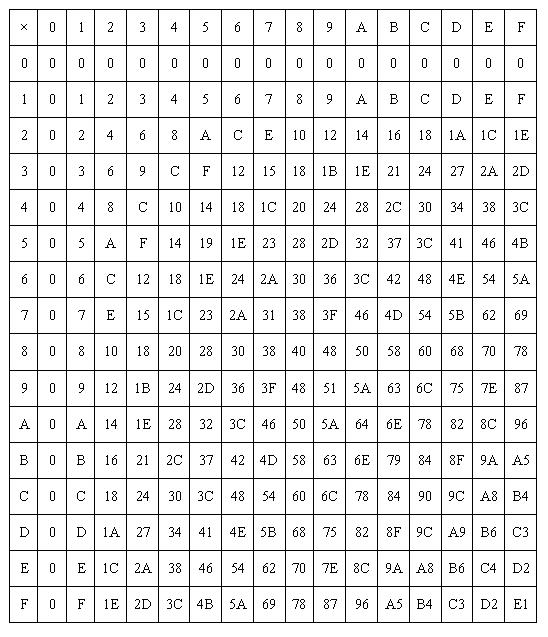
Таблица сложения и умножения чисел в шестнадцатеричной системе счисления .

БИЛЕТ 14

Булева алгебра — раздел математики, изучающий логические выражения и операции. Логические выражения представляют собой высказывания — некоторые утверждения, которым всегда можно сопоставить одно из двух логических значений: ложь или истина (их можно обозначать как   и  ,   и  ,   и  ).

Логическая функция - это функция, которая устанавливает соответствие между одним или несколькими высказываниями, которые называются аргументами функции, и высказыванием которое называется значением функции.

Основные аксиомы и теоремы алгебры логики

_

1. Ā = А 2. А + 0 = А 3. А + 1 = 1 4. А + А = А 5. А + Ā = 1

6. А * A = A 7. A * 0 = 0 8. A * 1 = A 9. A * Ā = 0

10. А+В = В+А 11. А*В = В*А (переместительный закон)

12. (А+В)+С = А+(В+С) 13. (А*В)*С = А*(В*С) (сочетательный закон)

14. А*(В+С) = А*В+А*С 15. А+В*С = (А+В)*(В+С)

16. А+(А*В) = А 17. А*(А+В) = А

_ _ _____ _ _ _ _ ____ _ _

18. А+В = А*В 19. А+В = А*В 20. А*В = А+В 21. А*В = А+В

_ _

22. А*В+А*В = А 23. (А+В)*(А+В) =А

_ _

24. 1 = 0 25. 0 = 1

БИЛЕТ 15

Таблица истинности для конъюнкции.

A	B	F
1	1	1
1	0	0
0	1	0
0	0	0

Таблица истинности для дизъюнкции.

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

Логическая операция исключающее ИЛИ (XOR).

a(бит 1)	b(бит 2)	a(бит 1) ^ b(бит 2)
0	0	0
0	1	1
1	0	1
1	1	0

Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Все аксиомы логики.

		1 коммутативность, переместительность
		2 ассоциативность, сочетательность
3.1 конъюнкция относительно дизъюнкции	3.2 дизъюнкция относительно конъюнкции	3 дистрибутивность, распределительность
		4 комплементность, дополнительность (свойства отрицаний)
		5 законы де Моргана
		6 законы поглощения
		7 Блейка-Порецкого
		8 Идемпотентность
		9 инволютивность отрицания, закон снятия двойного отрицания
		10 свойства констант
дополнение 0 есть 1	дополнение 1 есть 0
		11 Склеивание