7. Консервативные и неконсервативные силы

Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное.

 Характерное свойство таких сил – работа на замкнутой траектории равна нулю:

 

К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное.

Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.

8. Потенциальная энергия.

 

Потенциальная энергия системы – это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил.

Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.

Е_П1 - Е_П2 = Е_П = А_12конс, .

 

Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.

 

.

Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.

Её связь с силой

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы  , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии  . Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

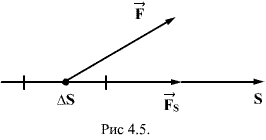
Для установления этой связи вычислим элементарную работу  , совершаемую силами поля при малом перемещении   тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой  . Эта работа равна

где  - проекция силы   на направление  .

Поскольку в данном случае работа совершается за счет запаса потенциальной энергии  , она равна убыли потенциальной энергии   на отрезке оси  :

Из двух последних выражений получаем

Откуда

Последнее выражение дает среднее значение   на отрезке  . Чтобы

получить значение   в точке нужно произвести предельный переход:

Так как   может изменяться не только при перемещении вдоль оси  , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от   по  :

Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

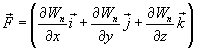
в математике вектор  ,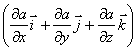

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом  .Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком

(4.15)