6 Толқындардың поляризациялауы. Толқындардың поляризациялауының жеке жағдайлары.
Электромагнит толқынның екі құраушысы болсын
(1.1)
Сонда
жалпы вектор
және
жақтары бар тікбұрыштың диагонал бойымен
қозғалады.
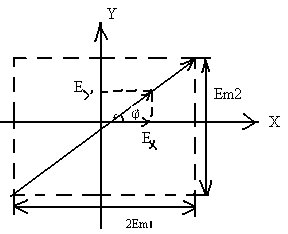
1.1сурет
Толқынның поляризация жазықтығы х осімен <р бүрышын қүрайды.
Егер
де
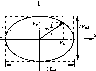онда
нәтижелік вектор өзінің соңымен эллипс
түрін сызып, w жиілікпен айнала бастайды.
1.2 сурет - Эллипстік поляризацияланған жазық элекгромагнит толқынның қүрылуы
Осындай толқын поляризацияланған деп aтaлaды,
бар
толқын оң поляризацияланган
толқын деп аталады.Ол комплекстік түрде мынаған тең:
(1.2)
Сонда
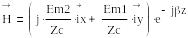(1.3)
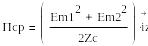(1.4)
болғанда,
шеңберлік пояяризацияланған толқынды
аламыз. ,
Сонымен қатар эллипсттік поляризацияланған толқындардың жалпы саны ретінде, әр түрлі бағытта айналып түратын, сызықты поляризацияланган толқынды алуға болады.
7. Эмп векторлары үшін шекті шарттар. Нормалды құраушылар.Тангесалды шарттар.
Магнит өрісінің нормалды және потенциалды қүраушы векторларының шектік шарттары
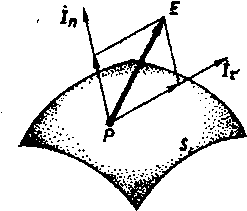
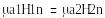
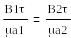
4.1 сурет .
Электр өрісінің нормалды және потенциалды қүраушы векторларьшың шектік шарттары
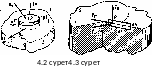
(4.2)
Егер бөлу шекарасының меншікті тыгыздығы аз болатын электрлік үстінгі қабаттық заряд бірқалыпты үлестірілген болса, онда (4.3)
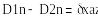
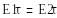
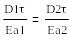
8. Шекті шарттардың толық жүйесі:
Магнит өрісінің нормалды және потенциалды қүраушы векторларының шектік шарттары
4.1 сурет .
Э
лектр
өрісінің нормалды және потенциалды
қурашы векторларьшың шектік шарттары
(4.2)
Егер бөлу шекарасының меншікті тыгыздығы аз болатын электрлік үстінгі қабаттық заряд бірқалыпты үлестірілген болса, онда (4.3)
9. Екі ортаның бөліну шегіне жазық электр магнитті толқындардың түсуі. Снелл заңы.Френель коэффициенті.Брюстер бұрышы.Толық ішкі шағылубұрышы.
Өте жақсы өткізетін жазықтыққа жазық электрмагнит толқынның нормалды түсуі
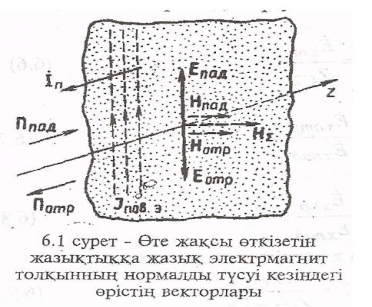
(6.1)
(6.2)
Д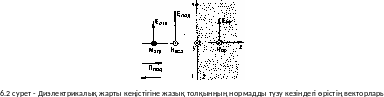
иэлектрикалық
жарты кеңістігіне жазық электрмагнит
толқынның нормалды түсуі Z<0 жарты
кеңістігі (1 - аудан) вакуум (
,
)
болып, ал z>0 жарты кеңістігі (2 - аудан)
магнитдиэлектрик (
,
)
болып саналады (6.2- сурет).
Қүламалы
толқын:
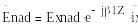
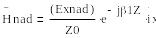
Мұндағы
Бейнеленген толқын:
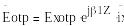
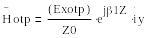
Сынған толқын:
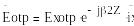
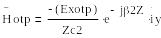(6.5)
мұндағы,
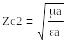
Бөлу шекарасында z=0 болғанда
немесе
Бейнелеу коэффиценті
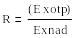(6.7)
Сыну коэффиценті
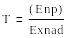(6.8)
(6.7) және (6.8) ескеріп, теңдеулер жүйесін шешіп, аламыз:
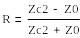
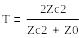(6.9)
Жеке жағдай (
,
)
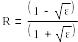
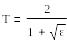(6.10)
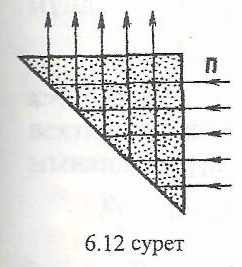
Снелли
заңы бойынша
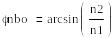болсын,
жағдайында
мөлшері sin\|/>l болады. Егер сыну бүрышы
ақиқат сан болса, онда мүндай жағдай
мүмкін емес. Бірақ комплексттік
аргументтің синусы әр түрлі, соның
ішінде соншалықты үлкен, ақиқат мәндерді
қабыдцай алады. Сондықтан формалды
түрде ф>фПВо болғанда, сыну бүрышы
vj/=90°+ja деп есептейміз.
Бірақ
(6.31)
Сонда
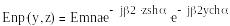
Жазық
толқын координаты бойымен таралады, ал
z координата бойымен экспонент бойынша
азаюын байқаймыз. Осындай толқынды
бірыңғай емес немесе беттік жазық толқын
деп атаймыз. Өйткені
Бірьщғай
жазық толқынның фазалық жылдамдығы
/(32, ал беттік толқынның фазалық жылдаадығы
әрқашан бірыңғай жазьщ толқьшның фазалық
жылдамдығынан аз боладьі. Сондықтан
беттік толқындарды тағыда баяу толқындар
дегг атайды. Ф=90° болғанда
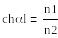
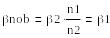
Беттік толқьшның фазалық жылдамдығы біршама тығыз ортадағы фазалық жылдамдыққа тең. Өрістің амплитудасы е=2.718 есе азаятын, z координаты бойының арақашықтығын өту терендігі деп атайды.
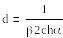6.33)
Біршама тыгыз ортада элеткромагнит әрісі қалыңдығы бір толқьшның үзындығына тең үстінгі қабатга болады. ф бүрьшіының өсуімен баііулау екпінді болады, ал біршама тығыз ортаға өрістің өту тереңдігі қысқарады.