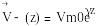- •1 Электр динамикасының негізгі заңдары. Материалды теңдеулер.
- •6 Толқындардың поляризациялауы. Толқындардың поляризациялауының жеке жағдайлары.
- •7. Эмп векторлары үшін шекті шарттар. Нормалды құраушылар.Тангесалды шарттар.
- •8. Шекті шарттардың толық жүйесі:
- •10 Қабаттар жүйесінен шағылысу. Жеке жағдайлар.
- •12. Электр магнитті өрістің көлденең құраушылары арасындағы байланыс. Тікбұрышты металлдан жасалған толқын өткізгіш.
- •13 Нmn типті толқынның эмп құрылысы. Толқын өткізгіштегі толқын ені, толқынды көлденең.
- •14 Екі ортаның бөліну шегіне жазық электр магнитті толқындардың түсуі.
- •15 Тікбұрышты толқын өткізгіштегі беткі токтар.
- •1 Домалақ толқын өткізгіштегі толқындар диаграммасы. Домалақ толқын өткізгішіндегі тасымалданатын қуат.
- •3 Металлдан жасалған домалақ толқын өткізгіш, н11 типті толқын. Бессель теңдеуі. M и n индекстерінің физикалық мәні.
- •4. Коаксиалды толқын өткізгіш. Коаксиалды толқын өткізгішіндегі толқындардың жоғары типтері. Коаксиалды толқын өткізгішті қолдану ерекшеліктері.
- •5. Тасымалдаудың линиялары. Квази т-типті толқын.
- •6. Диэлектрлі толқын өткізгіштер. Диэлектрлі толқын өткізгіштердің сипаттамасы.
- •7. Электр магнитті энергияны тасымалдау линияларындағы шығындар.
- •8.Тікбұрышты толқын өткізгішіндегі сыртқы токтар. Тікбұрышты және цилиндрлі толқын өткізгіштеріндегі өшу.
- •9. Тікбұрышты толқын өткізгіштегі толқындар типтерінің диаграммасы. Н10 толқыны. Тікбұрышты толқын өткізгіштегі тасымалданатын қуат.
- •10. Коаксиалды толқын өткізгішіндегі өшу. Жолақ линиясындағы өшу.
- •11 Ақырғы ұзындық линияларындағы электр магниттік толқындардың таралуы. Ақырғы ұзындық линиясының пәк.
- •12 Электр магнитті тербелістердің қоздырылуы. Электр магнитті тербелістердің қоздыру құрылғыларына қойылатын негізгі талаптар. Токты жиектеме. Байланыс тесіктері.
- •15 Диэлектрикті толқынды өткізгіштер ретінде талшықты-оптикалық жарық өткізгіш. Жарық өткізгіштердің негізгі сипаттамалары және оларды қолдану ерекшеліктері.
1-блок
1 Электр динамикасының негізгі заңдары. Материалды теңдеулер.
Электродинамика - ол электромагнит өрісін зерттейтін ғылым. Өрістің көзі - электр зарядтары. Қарапайым бөлшектердін электронның заряды - е = 1,602 •10-19/Кл. Электрмагнит өрісі жеке жағдайда элекгрлік немесе магниттік болуы мүмкін. Вакуум ішіндегі электр өрісінің кернеуі Е, q зарядқа күшпен әсер етеді
![]() (1.1)
(1.1)
мүндағы г - радиус-вектор, күштің әсер ету бағытын көрсетеді;
өлшем бірлігі - Е(В/м).
Вакуум ішіндегі электрлік ығысу (индукция) векторы
![]() Кл/м
(1.2)
Кл/м
(1.2)
мүндағы г0 = 8,842•10-12Ф/ж - электр тұрақтысы.
Вакуум ішіндегі магнит өрісін магнит индукциясының векторымен бейнелейді;
![]() ,Тл
(1.3)
,Тл
(1.3)
мүндағы µ== 4π·10 -7 =1,257•1о-6Гіі/м - магнит тұрақтысы;
Н – магнит өрісі кернеулігінің векторы.
Өткізгіштік ортадағы өткізгіш тоқтың тығыздығы
![]() ,А/м2,
(1.4)'
,А/м2,
(1.4)'
мүндагы σ - заттың салыстырмалы өткізгіштігі. (1.4) өрнегі Ом заңының дифференциаддық түрі.
Тұйықталған V көлемнің S бeтімен шектелген р зарядыньң шамасы
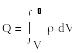 (1.5)
(1.5)
мұндағы р - зарядтың'көлемдік тығыздығы.
Егер көлем ішіндегі. зарядтың шамасы өзгерсе, онда бұл кеңістікте өткізгіш тоқ туады.
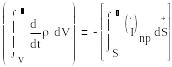 (1.6)
(1.6)
Остроградский - Гаусс теоремасы бойьшпіа
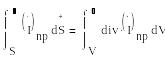
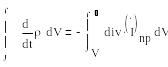 (1.7)
(1.7)
Егер V–›0 болса, онда
 (1.9)
(1.9)
Бұл теңдеу үздіксіз өткізгіш тоқ теңдеуі деп аталады;
S тұйык беті арқылы өтетін заряд тудырған В векторлық өрісі ағыны заряд шамасьның электр тұрақтысының қатынасына тең:
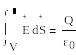 (1.10)
(1.10)
Сфералық бет үшін;
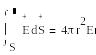 (1.11)
(1.11)
Осыдан


мүндағы а - сфералық беттің радиусы.
Гаусс заңының дифференциалдық түрі:
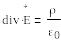 (1.12)
(1.12)
S тұйықталған бетімен шектелген туынды көлемге ағып кіретін магнит ағыны, одан ағьп шығатын ағынға тең
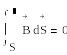 (1.13)
(1.13)
Дифференциалдық түрінде .
![]()
Н магнит өрісінің кернеулік векторының циркуляциясы L контурының бойымен ағатын толық тоққа тең. (1.14)
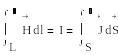 (1.14)
(1.14)
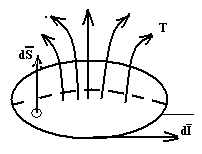
сурет толық тоқтың заңын тұжырымдау
Векторлық анализден Стокс теоремасын пайдаланып, аламыз
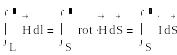
Осынның
нәтижесінде өз бетімен таңдаған
контурдан толық заңын
дифференциалдық түрде аламыз
![]() (1.15)
(1.15)
Ығысу тоғы зарядтың өзгеруінен пайда болады;ал сонымен қатар тоқ көзіне қосылған- конденсатордың астарының арасында электр өрісінің кернеулігіне тең.
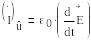 (1.16)
(1.16)
Қай бір тұйық L контурдан өтетін магнит өрісінің әртүрлі өзгерісі, осы контурда Ё кернеулігімен электр өрісін туғызады
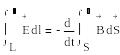
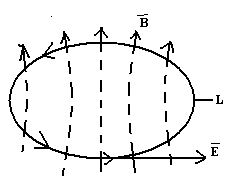
1.2 сурет - Электромагниттік индукция заңы
Осы
мөлшерді
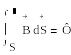 магнит ағыны деп атайды.
магнит ағыны деп атайды.
Стокс теоремасын пайдаланып, мына формулаға ие боламыз
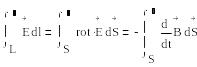
Осыдан электромагниттік индукция заңының дифференциалдық түрін
 (1.18)
аламыз.
(1.18)
аламыз.
Электрмагнит өрісінің материалдық теңдеулері.Диэлектриктің ішінде ығысу векторы мен электрлік өріс кернеулігінің арасындағы байланыс мына түрде болады
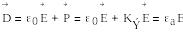
мүндағы Р - поляризация векторы;
Кэ - заттың диэлектрлік қабілеттілігі;
ɛа=ɛ0+Kэ абсолюггі диэлектрлік өтімділігі. Салысгырмалы диэлектрлік отімділігі
ɛ=ɛа/ɛ0 (1.20)
Ферромагнетикте сыртқы өрісі бар магнит индукциясының мөлшері
мынаған тең
 (1.21)
(1.21)
мүндагы М - заттың магниттелуі;
Км- заттың магниттік қабілеттілігі;
µа - заттың абсолютті магниттік өтімділігі.
Заттың салыстырмалы магниттік өтімділігі
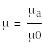
Диамагнетикте және парамагнетикте µ≈1, ферромагнетикте µ»1.
Магнит өрісінің кернеулігі 100 А/м көп болғанда, ферромагнетиктің магниттелу қисығы түзу сызықты емес болады. Диэлектрикте электр өрісінің жоғарғы кернеулігінде электрлік көшкіндік тесіп өту пайда болады, осымен қатар D(E) тәуелділігі түзу сызықты емес болады. Анизатроптық деп әр түрлі бағытта ортаның қасиеттері үқсас емес болып келетін ортаны айтамыз. Олар үшін материалдық теңдеулер келесі түрде жазылады:
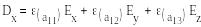
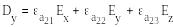
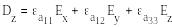
B͞(H͞) магнит өрісі үшін материалдық теңдеулер үқсас болып келеді.
2.Толқындар. Электромагнитті толқындар. Шығыны жоқ ортадағы толқындар. Айнымалы электромагниттік өріс тербелістерінің кеңістікте таралуын электромагниттік толқын деп атайды. Максвеллдің болжамы бойынша электромагниттік толқын тогы бар өткізгіштің бойымен, диэлектрикте және электр зарядтары жоқ вакуумде де тарала алады. Максвелл теориясынан шығатын аса маңызды салдардың бірі — электромагниттік толқынның таралу жылдамдығының шектілігі. Оның есептеулері бойынша электромагниттік толқынның таралу жылдамдығы:
 мұндағы
мұндағы
 Ф\м
— электрлік және
Ф\м
— электрлік және  Гн\м—
магниттік тұрақтылар. Бұл электромагниттік
өрістің іргелі қасиеті. Электромагниттік
толқынның ортадағы таралу жылдамдығы
Максвелл формуласы бойынша анықталады:
Гн\м—
магниттік тұрақтылар. Бұл электромагниттік
өрістің іргелі қасиеті. Электромагниттік
толқынның ортадағы таралу жылдамдығы
Максвелл формуласы бойынша анықталады:
 мұндағы
мұндағы  —
ортаның сыну көрсеткіші,
—
ортаның сыну көрсеткіші,  —
ортаның диэлектрлік және
—
ортаның диэлектрлік және ![]() —
магниттік өтімділіктері..
—
магниттік өтімділіктері..
Шығыны жоқ магнит диэлектрик ортағы толқындар
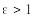
![]()
![]()
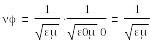
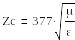
3.Толқындар. Электромагнитті толқындар. Шығыны аз ортадағы толқындар. Жақсы өткізетін ортадағы толқындар. Айнымалы электромагниттік өріс тербелістерінің кеңістікте таралуын электромагниттік толқын деп атайды. Максвеллдің болжамы бойынша электромагниттік толқын тогы бар өткізгіштің бойымен, диэлектрикте және электр зарядтары жоқ вакуумде де тарала алады. Максвелл теориясынан шығатын аса маңызды салдардың бірі — электромагниттік толқынның таралу жылдамдығының шектілігі. Оның есептеулері бойынша электромагниттік толқынның таралу жылдамдығы:
мұндағы Ф\м — электрлік және Гн\м— магниттік тұрақтылар. Бұл электромагниттік өрістің іргелі қасиеті. Электромагниттік толқынның ортадағы таралу жылдамдығы Максвелл формуласы бойынша анықталады:
мұндағы — ортаның сыну көрсеткіші, — ортаның диэлектрлік және — магниттік өтімділіктері..
Аз шығыны бар диэлектрик ортадағы толқындар

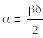
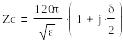
![]()
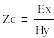 қатынасы
ортаның сипаттамалық толқындық
қатынасы
ортаның сипаттамалық толқындық
кедергісі деп аталады. Е және Н синфазды емес тербеледі, Zс- комплекстік сипаттаманы білдіреді, жылжу бұрышы ϭ/2 радианға тең, ягни соншалықты аз болғандықтан, оны практикада қолданбауға да болады.
4 Максвелл теңдеулері бойынша ақпар: екі жақтық ауыстырылу принципі. Максвелл тендеулері.Толық тоқ заңы
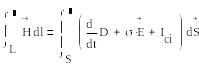 (1.1)
(1.1)
Электрмагниттік индукция заңы
(1.2)
Гаусс заңы
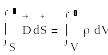 (1.3)
(1.3)
Магнит өрісінің күш сызықтарының үздіксіздік заңы
(1.4)
Ортаның қасиеттерін көрсететін теңдеулер
 (1.5)
(1.5)
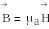 (1.6)
(1.6)
Дифференциалдық түрдегі Максвелл тендеулері:

![]()
![]() (1.7)
(1.7)
Гармоникалық тербелістер үшін Максвелл тендеулері
Әр түрлі өріс векторының, мысалы, электр өрісінің кеңістікте берілген нүктесінде, гармоникалық заң бойынша өзгеруі осылай жазылады: _ _
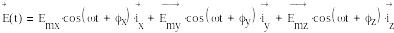 1.8
1.8
Өрістің комплекстік амплитудасы мынаған тең болады
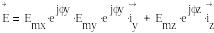 (1.9)
(1.9)
Осымен
қатар
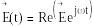 (1.10)
(1.10)
Комплекстік түрде Максвеллдің диффсренциалдық тендеулері осылай көрсетіледі:
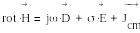


![]() (1.11)
(1.11)
Материалдық ортадагы салыстырмалы өткізгіштіктің соңғы мәнімен электрмагнит процессін қарастырайық. (1.11) жүйенід (1) және (5) теңдеулерін біріктіре отырып келесі формулаға ие боламыз.
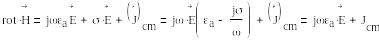
з аттың
комплекстік диэлектрлік өткізгіштігі
деп аталады.
аттың
комплекстік диэлектрлік өткізгіштігі
деп аталады.
Жақсы диэлектриктер үшін ӨЖЖ-диапазонындағы жиілікте tg ϭ≈ 10 -4 /10 -5 болады.S түйық бетімен шектелген, V берілген көлемінен электрмагнит өрісінің қуатының ағыны мынаған тең болады:
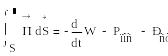 (1.13)
(1.13)
Мұндағы П͞ = |E͞H͞] - өріс қуат ағынының тығыздық векторы,
Пойнтинг векторы (1.14);
W - өріс энергиясы;
Pnoт - жылулық шығынның қуаты;
Рст - шет жақ энергия көздерінің қуаты;
(1884 ж. ағылшын галымы Дж. Пойнтинг (1.14) тендігін есептеп шығарды).
Өріс энергиясының көлемдій тығыздығы
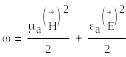 (1.15)
(1.15)
Жылулық шыгынның қуатының көлемдік тығыздығы
Рпот=ϭЕ͞2 (1.16)
Шет жақ энергия көздерінің қуатының көлемдік тығыздығьг
Рст=I͞cтЕ͞ (1.17)
Пойнтингтің комплекстік векторы
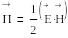
Бір мерзім ішіндегі қуат ағынның орташа тығыздығы
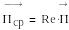
Қуат ағынының тығыздығының тербеліп түрған құрамы
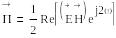
5 Жазық электр магниттік толқындар. Таралу коэффициенті, фаза коэффициенті, жазық электр магниттік толқынның өшу коэффициенті. Жазық электр магниттік толқынның фазалық, топтық жылдамдықтары. Толқындық кедергі.
Жазық
толқынның математикалық моделі

мүндағы Vm - толқынньщ амплитудасы;
w
- толқынның бұрыштық жиілігі,
![]()
z - сызықтық координатасы;
в - толқын фазасының коэффициенті
λ- толқынның ұзындығы.

1.1 сурет. Өрістің уақыт бойынша өзгеруі
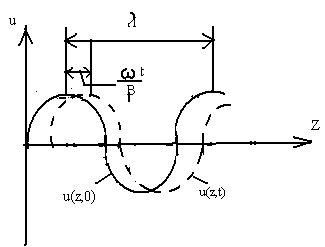 1.2
сурет - Өрістің кеңістікте өзгеруі
1.2
сурет - Өрістің кеңістікте өзгеруі
Толқындық фронт дегеніміз z толқынның таралу осіне перпендикуляр болатын жазықтық. Әртүрлі t үшін бүл жазықтықтың координатасы мына тендікті қанағаттандырады:
![]() (1.3)
(1.3)
Фазалық жылдамдық деп толқындық фронт ауысуының жылдамдығын айтады
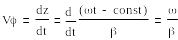 (1.4)
(1.4)
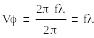 (1.5)
(1.5)
 (1.6)
(1.6)
Осындай толқынның фазалык жылдамдығы:
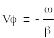 (1.7)
(1.7)
яғни, ол z координатасының азаю жағына ауысады.
Материалдық' орталарда жылульіқ шығынның. есебінен толқынның амплитудасы өшеді
![]() (1.8)
(1.8)
мүндағы a - ортаның ішіндегі толқынның өшу коэффиценті.
Техникалық есептеулерде өшу бойын пайдаланады.
 (1.9)
(1.9)
Сондықтан, материалдық ортадағы жазық толқынның теңдеуі

 (1.10)
(1.10)
1.3 сурет - Материалдық ортадағы толқынның қисьіғы
Комплекстік түрде:
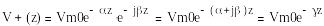 (1.11)
(1.11)
мүндағы
![]() -
таралу коэффиценті деп аталады. Z
координатасының азаю жағына тарайтын
толқын үшін
-
таралу коэффиценті деп аталады. Z
координатасының азаю жағына тарайтын
толқын үшін