Приклад 8
Служба менеджменту складу відділення фірми «Девис» використає регресії часові серії для прогнозу різних продажів у наступних чотирьох кварталах. Оцінки продажів для кварталів: $100000; $120000; $140000 й $160000 Сезонні індекси для чотирьох кварталів визначені: 1,30; 90; 70 й 1,15 відповідно.
Розраховуючи сезонний прогноз продажів або з регульованим трендом, ми повинні помножити кожен сезонний індекс на відповідний трендових прогноз:
Y сезонний = Індекс х Y трендовий прогноз.
Отже, для
кварталу 1: Y1 = (1.30)($100 000) =$130 000;
кварталу 2: Y2 = (.90)($120 000) = $108 000;
кварталу 3: Yз = (.70)($140 000) = $98 000;
кварталу 4:4 = (1.15)($160 000) = $184 000.
Приклад 9 забезпечує третю ілюстрацію сезонності даних
ПРИКЛАД 9
Для іншого приклада оцінки лінії тренда й сезонного регулювання ми запозичили відомості з госпіталю, які використали 66-місячні дані про дорослих стаціонарних хворих, і одержали наступне рівняння:
Y = 8091+21,5Х,
де Y— пациенто-дни; X— час, міс.
На базі цієї моделі госпіталь прогнозує пациенто-дні для наступного місяця (період 67):
Пациенто-дни = 8091 + 21.5 (67) = 9530 (тільки використовуючи тренд).
Тому що ця модель визначає лінію зростаючого тренда в попиті на обслуговування пацієнтів, вона ігнорує сезонність, що на сьогодні відома адміністрації. Таблиця, наведена нижче, містить поточні сезонні індекси, що базуються на тих же 66 місяцях. Такі сезонні дані, як ці, є типовими для госпіталів. Помітимо, що в січні, березні, липні й серпні проявляються особливо високі в середньому кількості пациенто-дней, а лютий, вересень, листопад і грудень показують зниження кількості пациенто-дней.
-
Місяць
Сезонний індекс
1
1,04
2
0,96
3
1,02
4
1,008
5
0,99
6
0,99
7
1,03
8
1,04
9
0,96
10
1,0095
11
0,9585
12
80,98
Коректуючи часові серії екстраполяцією з урахуванням сезонності, госпіталь множить місячний прогноз на відповідний сезонний індекс. Так, для періоду 67, яким був січень,
Пациенто-дні = (9530)( 1.0436) = 9946 (тренд із урахуванням сезонності).
Використовуючи цей метод, були прогнозовані пациенто-дні із січня по червень (періоди з 67 по 72) як 9946, 9236, 9768, 9678, 9554 й 9547. У цьому прикладі краще прогнозуються пациенто-дні, так само як більш точно прогнозуються бюджетні витрати.
6. Методи регресійного і кореляційного аналізів
Моделі причинного прогнозування звичайно містять ряд змінних, які мають відношення до пророкування змінного. Як тільки ці змінні будуть знайдені, будується статистична модель, що використається для прогнозу цікавляючої нас змінної. Цей підхід є могутнішим, чим методи часових серій, які використають минулі значення для прогнозованої змінної.
Багато факторів могли б розглядатися в причинному аналізі. Наприклад, продаж товару можуть бути пов'язані з витратами фірми на рекламу, із призначуваною ціною, зі справами конкурентів і стратегіями просування товарів або навіть із економічними умовами й безробіттям. У цьому випадку продажу буду! називатися залежної змінної, а інші змінні буду" називатися незалежними змінними. Робота менеджерів полягає у встановленні найкращої статистичної залежності між продажами й незалежними змінними. Найбільш загальною кількісною моделлю причинного прогнозована є модель лінійного регресійного аналізу.
Використання регресійного аналізу для прогнозування. Ми можемо використати такі математичні моделі, які застосовували як метод найменших квадратів у трендовому проектуванні, перетворивши їх до моделей лінійної регресії Залежна змінна, котру ми хочемо спрогнозувати, буде позначатися в. Але тепер незалежна змінна х — це не час.
в = а + bх,
де в — значення залежної змінної, тут — об'єм продажів;
а — відрізок, що відтинає на осі в,
b — нахил лінії регресії;
х— незалежна змінна.
ПРИКЛАД 10
Будівельна компанія реконструює старі будинки. Після закінчення часу компанія знайшла, що її обсяг робіт по реконструкції пов'язаний з рівнем місцевої заробітної плати. Таблиця нижче містить дані про річні доходи й суми грошових доходів в 1987-1992 голах.
-
Продаж
Заробітна плата
2
1
3
3
2,5
4
2
2
2
1
3,5
7
Служба менеджменту компанії хоче представити математичний взаємозв'язок, що буде допомагати їй пророкувати продажі. Перше, що необхідно визначити, чи має місце лінійний зв'язок між заробітною платою й продажами; для цього наносяться відомі дані на діаграму розсіювання.
На діаграмі показано шість крапок даних, які відбивають позитивну залежність між незалежною змінною, заробітною платою й залежним змінної, продажами. Коли зарплата зростає, продажу компанії мають тенденцію до підвищення.
Ми можемо знайти математичне рівняння регресії, використовуючи метод найменших квадратів.
-
Продаж
Заробітна плата
x2
xy
2
1
1
2
3
3
9
9
2,5
4
16
10
2
2
4
4
2
1
1
2
3,5
7
49
24
15
18
80
51,5
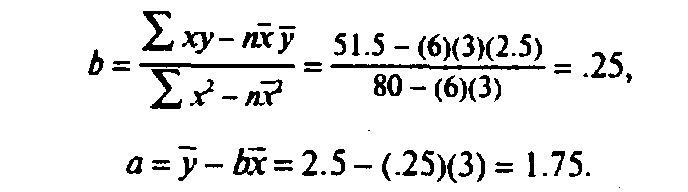
Рівняння регресії, отже, буде:
в =1.75 +.25х,
або:
Продажу = 1,75 + .25 Зарплата.
Якщо місцева комерційна служба визначить, що зарплата в регіоні буде $ 600 000 000 у наступному році, ми можемо прогнозувати продажу будівельної компанії по рівнянню регресії:
Продажу (у млн $) = 1.75 + .25 (6)
або:
Продажу = $325 000.
Заключна частина приклада 10 ілюструє головну слабість методів прогнозування на базі регресії. Навіть коли ми розрахували рівняння, необхідно проводити прогноз незалежної змінної х (у цьому випадку заробітної плати), перш ніж визначати залежну змінну y для наступного періоду часу. Хоча це - проблема не для всіх прогнозів, варто уявляти собі складності у визначенні майбутніх значень таких загальних незалежних змінних, як рівень безробіття, валовий національний продукт, індекси цін і т.д.
Прогноз продажів $325 000 у прикладі 10 називається крапкою оцінки для в. Крапка оцінки є реальним значенням, або очікуваною величиною, можливих об'ємів продажів дистриб'юторів. Рис. 4.6 ілюструє цей підхід.
Рис. 4.6. Стандартна помилка відхилення
Вимірюючи точність регресійних оцінок, нам необхідно розрахувати стандартну помилку прогнозу Sy,x. Її називають стандартним відхиленням рівняння регресії. Рівняння (4.11) ми знаходимо в більшості книг по статистиці для розрахунку стандартного відхилення арифметичних значень:
де Y — значення Y для кожної крапки даних;
Yc — розрахункове значення залежної змінної з рівняння регресії;
п — число крапок даних.
Рівняння (4.12) може здатися більше загальним, але це тільки версія рівняння (4.11). Та й інша формули вимагають загальних даних і можуть бути використані на прогнозованих інтервалах навколо оцінюваної крапки.
Коефіцієнти кореляції для лінії регресії. Рівняння регресії - це один зі шляхів установлення природи взаємозв'язку між двома змінними. Рівняння показує, як один змінна відбивається на значенні й змінах інший змінної.
Інший шлях установлення відносин між двома змінними полягає в розрахунку коефіцієнтів кореляції. Цей вимірник показує ступінь, або силу, лінійного взаємозв'язку. Звичайно позначуваний як r, коефіцієнт кореляції може бути деяким числом між +1 й -1. Рис. 4.7 ілюструє різні можливі значення r.
мал. 4.7. Чотири значення коефіцієнта кореляції:
а) позитивна кореляція г = +1; Ь} позитивна кореляція 0 <<• < 1:
с) немає кореляції г = 0; з1) негативна кореляція г = -1
Розраховуючи r, ми використаємо багато тих даних, які необхідні для розрахунку а й b у рівнянні регресії. Більше протяжне рівняння для r наступне:
ПРИКЛАД 12
У прикладі 10 ми показали взаємозв'язок між замовленнями будівельної компанії й рівнем заробітної плати. Розраховуючи коефіцієнти кореляції для зазначених даних, ми можемо тільки підсумувати один розрахунковий стовпець (для y2) і потім звертатися до рівняння для г
r=0,91
Множинний регресійний аналіз. Множинна регресія — це практично розширення моделі, що ми тільки що розглядали. Вона дозволяє будувати модель із поруч незалежних змінних. Наприклад, якщо будівельна компанія хоче включати середню річну процентну ставку в її модель прогнозу продажів, що відповідає рівняння буде:
в = а + b1x1+b2x2 (4.14)
де в — залежна змінна, продажу;
а — відрізок, що відтинає на осі в;
x1 й x2 — значення двох незалежних змінних: зарплати й процентної ставки відповідно.
Математично множинна регресія вимагає комплексу засобів (звичайно із застосуванням комп'ютера), а формулу для визначення а, b2 й b2 ми знаходимо в підручниках по статистиці.
ПРИКЛАД 13
Нова лінія регресії, розрахована по комп'ютерній програмі, для будівельної компанії має вигляд рівності:
Y=1,80 +.30X1 +5.0X2.
Ми також знаходимо, що новий коефіцієнт кореляції .96, що означає включення змінної Хг, процентної ставки навіть більше підсилює лінійну залежність.
Ми можемо тепер прогнозувати продажу компанії, якщо знаємо значення заробітної плати й процентної ставки в наступному році. Якщо зарплата буде $600 млн і ринкова ставка .12 (12%), продажі будуть прогнозуватися як
Продажу (5 сотні тисяч) = 1.80 + .30(6) - 5.0 (.12) = 1.8 + 1.8 - .6 = 3.00, іли
Продажу = $300 000.