Формы представления переключательной функции
Нормальные формы – эти формы представляют дизъюнкции элементарных конъюнкций или конъюнкции элементарных дизъюнкций.
)
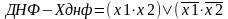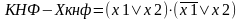
Любая функция имеет несколько ДНФ или КНФ. Однозначность представления функции возможна только при записи ее в совершенных нормальных функциях.
СДНФ – это логическая сумма всех переменных, для которых функция равна 1.
СКНФ – то логическое произведение всех переменных, для которых функция равна 0.
-
Х1
Х2
Х3
F(x1, x2, x3)
Хсднф и Хскнф
0
0
0
0
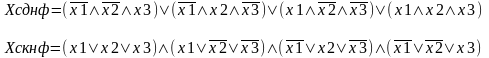
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
Минимализация функции алгебры логики (фал)
Логическую схему, реализующую заданный алгоритм, можно синтезировать по выражению СДНФ или СКНФ. Однако, полученная схема не оптимальна с точки зрения реализации. Исходное выражение минимализируют, цель – снижение стоимости реализации. Основной критерий – уменьшение количества элементарных элементов при разработке схемы, а также использование только однородных элементов типа и-не, или-не.
Минимализация – упрощение логического выражения с целью уменьшения числа членов и уменьшение числа аргументов в каждом члене. Выполнение процесса минимализации позволяет уменьшить число логических элементов на одном кристалле.
Минимализация возможна двумя основными путями:
а лгебраическая минимализация логических функций состоит в использовании аксиом, законов и тождеств алгебры логики. Аксиомы: 1+А=А, А + А=А, 0*А=0, А*А=0
Основные законы: А) дистрибутивные А(В+С)=АВ+АС
Б) Двойственности (Де Моргана) А+В=А*В, А*В=А+В
В) Соотношения: 1. поглощения А+А*В=А, А(А+В)=А
2. склеивания А*В+А*В=А, (А+В)(А+В)=А
Метод минимизации графический
Процедуру минимизации ФАЛ можно формализировать, если воспользоваться представлением в виде карт макстермов и минтермов . Распространение получили карты Карно или Вейче.
Карта – это таблица, число клеток которой соответствует числу переменных функции 2n. Каждому минтерму соответствует своя клетка, если нужно представить на карте логическую функцию, заданную в СДНФ, то в соответствующей клетке заносится 1, остальные заполняют 0.
Функция 2х переменных
Функция 3х переменных
Понятие «Базис»
При составлении схем из логических элементов, решаются задачи анализа и синтеза. Задача синтеза – выбор типов элементов, на которых будут реализованы заданные функции. Минимальный набор логических элементов, образующих функционально полную систему элементов, называют базис, т.е. с помощью элементов базиса можно реализовать сколь угодно сложную логическую функцию.
Основной базис (базис Буль)
Элементы И, ИЛИ, НЕ
Базис Шеффера
Элемент И-НЕ
Базис Пирса
Элементы ИЛИ-НЕ
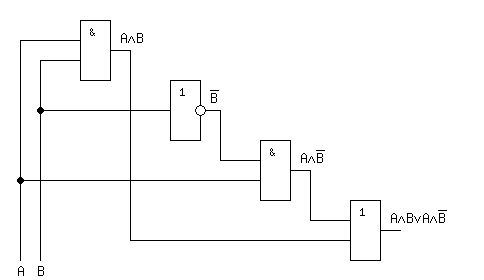
1 )y=A*B+A*B
