Свойства статически неопределимых систем.
1) В статически неопределимых системах усилия (внутренние силовые факторы) зависят от жесткости всех стержней системы, т.е. от их площадей сечения и модулей упругости. Это обстоятельство затрудняет расчет подобных систем, т.к. приходится предварительно задавать сечения стержней или соотношение сечений. Усилия в стержнях распределяются пропорционально их жесткостям.
2) Статически
неопределимые системы реагируют на
изменения температуры. Если система
была собрана при одной температуре, а
затем температура изменилась (для всей
системы или для некоторых ее элементов),
то возникают напряжения даже при
отсутствии внешней нагрузки. Эти
напряжения называют температурными
напряжениями. В статически определимых
системах подобное явление не происходит.
Составляя уравнения совместности
деформаций необходимо учитывать не
только силовую, но и температурную
деформацию. Для тех стержней системы,
которые подвергаются температурному
воздействию, удлинения определяются
- коэффициент
линейного температурного расширения
материала стержня;
- температурный
перепад в стержне.
3) В статически неопределимых системах, в отличии от статически
определимых, возникают так называемые монтажные напряжения, яв-
ляющиеся результатом сборки неточно изготовленных конструкций. Примеры.
Лекция IV Расчет систем, работающих на растяжение-сжатие, за пределами упругости.
Распространенный в практике расчета машиностроительных конструкций расчет по допускаемым напряжениям обладает существенным недостатком – он не дает представления об истинных запасах прочности конструкций.
Стремление сделать машину, инженерное сооружение и т.п. более легкой, экономичной приводит к необходимости рассматривать деформации за пределами упругости.
При расчете по методу допускаемых напряжений за предельное со-
стояние конструкции принимается такое состояние, когда напряжение
в одной из точек конструкции достигает предела текучести. Однако, если напряженное состояние неоднородно, т.е. меняется от точки к точке или разное для разных элементов конструкции, то появление пластических деформаций в одной из точек еще не означает наступление предельного состояния для всей конструкции.
Расшифруем уже использованное нами понятие предельного состояния. Под предельным состоянием конструкции понимают такое ее состояние, когда становится невозможной ее нормальная эксплуатация. Это следующее состояние:
1) Конструкция перестает сопротивляться воздействию внешних сил вследствие появления массовой текучести.
2) Разрушается, если конструкция изготовлена из хрупкого материала.
3) В конструкции появляются недопустимо большие перемещения.
В этой лекции мы будем рассматривать первое из этих состояний.
Схематизация диаграммы растяжения материала
Экспериментальной основой расчетов за пределами упругости являются испытания в условиях одноосного растяжения. Диаграмма растяжения такого пластичного материала, как малоуглеродистая сталь, имеет следующий вид.
Н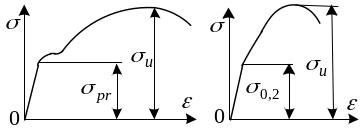
екоторые
стали, сплавы, цветные металлы обладают,
в достаточной мере, пластическими
свойствами, но площадка текучести у них
отсутствует.
Реальные диаграммы весьма сложны для расчета. Чтобы упростить задачу их схематизируют, т.е. заменяют отрезками прямых или кривых, имеющих простое математическое описание. В зависимости от вида реальных диаграмм возможны разные пути схематизации. Приведем некоторые из них.
1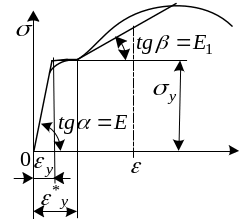
)
Схематизация диаграммой с площадкой
текучести и линейным упрочнением.
Напряжения и деформации здесь связаны
следующими зависимостями:
1) при
(закон Гука)
2) при
3) при
Здесь
- модуль упругости
- модуль упрочнения
- деформация,
соответствующая пределу текучести.
- деформация,
соответствующая началу упрочнения.
У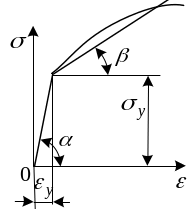
часток
упрочнения можно описать степенной
кривой, лучше приближающей соответствующий
участок реальной диаграммы. Тогда мы
получим диаграмму с площадкой текучести
и степенным упрочнением. Связь между
напряжениями и деформациями на последнем
участке в этом случае выглядит: при
;
,
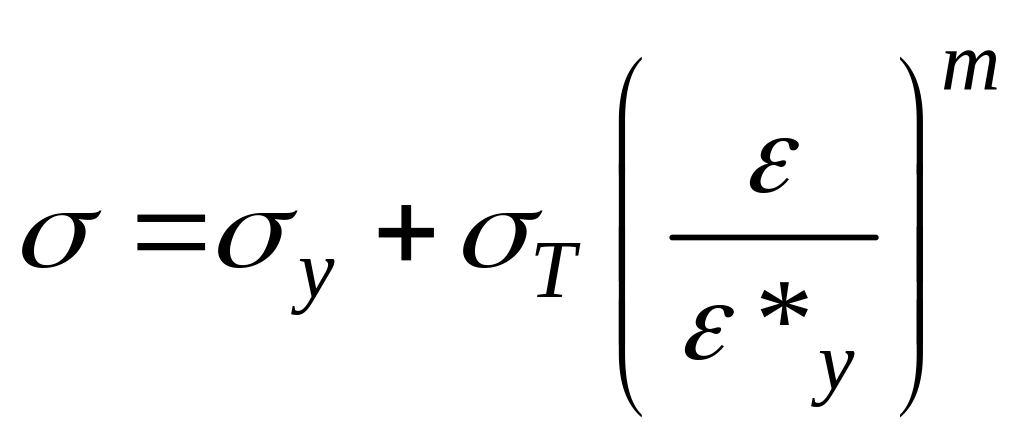где
2) Диаграмма с
линейным упрочнением. Она используется
в том случае, если схематизируемая
диаграмма не имеет площадки текучести.
Связь между
напряжениями и деформациями в этом
случае очевидна. Разумеется, что закон
упрочнения и в этом случае можно принять
степенным. Но чаще всего мы будем
использовать диаграмму идеального
у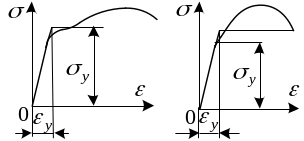
пругопластического
материала, согласно которой материал
вплоть до
идеально упруг (следует закону Гука), а
затем идеально пластичен. Эту диаграмму
можно рассматривать как частный случай
предыдущей при модуле упрочнения равном
нулю. Она используется в случае, когда
материал имеет развитую площадку
текучести либо в случае, когда она
достаточно точно аппроксимирует реальную
диаграмму.