Деформированное состояние при растяжении и сжатии
Т.к. напряженное состояние однородно, то однородным будет и деформированное состояние. Любой элемент объема будет деформироваться одинаково. Поперечные сечения стержня останутся плоскими, и будут удаляться друг от друга при растяжении и сближаться при сжатии. Этот факт можно положить в основу всей теории и сформули-ровать как гипотезу плоских сечений: сечения плоские и нормальные к оси до деформации остаются плоскими и нормальными к оси после деформации.
Определим удлинения и деформации, возникающие в стержне.
П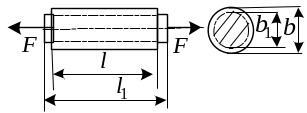
усть
-длина
стержня до деформации,
-
длина стержня после деформации. Величину
называют продоль-ным удлинением.
Т.к. деформированное состояние однородно,
то деформация не зависит от базы
измерения. Деформация в направлении
оси стержня равняется:
(2). Эта величина называется относительным
удлинением стержня.
Продольная
деформация (в направлении оси стержня)
сопровождается поперечной:
,
где
- характерный
размер поперечного сечения до деформации;
- то же самое после
деформации.
Знаки продольной и поперечной деформаций противоположны. Продольное удлинение сопровождается уменьшением поперечных
размеров и наоборот.
Отношение деформации поперечной к деформации продольной есть для данного материала величина постоянная, называется
коэффициентом
Пуассона.
Оценим величину
коэффициента Пуассона. При растяжении
стерж-ня его длина увеличилась в отношении
,
а линейные размеры сечения уменьшились
в отношении
,
следовательно, площадь поперечного
сечения уменьшилась в отношении
.
Относительное изменение объема равно:
-
Т.к. деформации
малы, то удержим в выражении лишь их
первые степени
.
Т.к. при растяжении объем должен
увеличиться, то
,
,
т.е. коэффициент Пуассона по величине
не превышает
.
Для сталей эта величина колеблется в
пределах 0,25 – 0,35.
Связь между напряжениями и деформациями. Закон Гука.
Как упоминалось ранее, между напряжениями и деформациями су-ществует связь, которая может быть установлена лишь экспериментальным путем.
Большинство твердых тел, при сравнительно небольших нагрузках, обнаруживают свойство однозначной зависимости между напряжениями и деформациями (или между силами и перемещениями).
Н
апример,
если вспомнить известные нам диаграммы
растяжения и сжатия малоуглеродистой
стали, то можно заметить, что вплоть до
значений напряжения равного
-
предела пропорциональности зависимость
между напряжениями и деформациями
близка к линейной.
Подобная картина наблюдается и у других сталей, а также, может
быть менее отчетливо, у других материалов. Данный эксперименталь-
ный факт позволяет принять простейший из упругих законов – закон Гука, т.е. закон линейной упругости:
Напряжения
пропорциональны деформациям
Коэффициент
пропорциональности между напряжениями
и деформациями
называется модулем упругости первого
рода (модулем Юнга). Модуль упругости
определяется опытным путем и служит
мерой жесткости материала. Геометрический
смысл
-
угловой коэффициент прямолинейного
начального участка диаграммы материала.
Модуль упругости для некоторых, часто применяемых материалов, имеет приблизительно следующие значения.
Сталь:
;
Медь:
;
Дерево:
;
Каучук:
Отметим еще раз, что свойство упругости, в частности линейной упругости, относительно. Уместно говорить не о упругих и неупру-гих материалах, а о упругом и неупругом состоянии материала.
Если в (3) выразить
по формуле (2) и учесть (1), то получим
закон Гука в форме, позволяющей находить
удлинения.
Величину
называют жесткостью при растяжении-сжатии.
Закон (4) можно сформулировать следующим
образом: удлинение стержня прямо
пропорционально нормальной силе и длине
стержня и обратно пропорционально
жесткости при растяжении-сжатии.
По формуле (4) можно определять удлинения только в том случае, если нормальная сила и поперечное сечение постоянны по длине стержня, т.е. если напряженное состояние однородно.
Е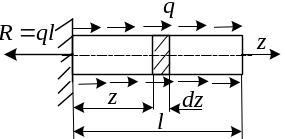
сли
нормальная сила и поперечное сечение
меняются по длине ступенчато, то стержень
надо разбить на участки, так чтобы в
пределах каждого участка
и
были постоянны, определить удлинение
каждого из участков и тогда полное
удлинение стержня будет равняться
алгебраической сумме, (знак определяется
знаком
)
удлинений участков.
Если напряженное
состояние в стержне неоднородно, то
выделив малый элемент длиной
определим
его удлинение
.
Здесь
и
рассматривается как функции z.
Полное удлинение стержня будет равно:
.Напряженное состояние при растяжении и сжатии.
В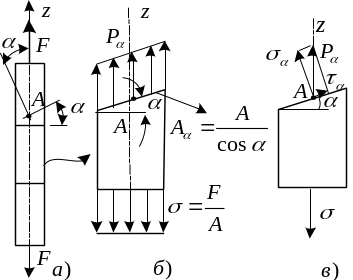
о
вводной лекции мы уже упоминали о
напряженном состоянии в точке и в
частности, говорили, что знать напряженное
состояние в точке – это уметь вычислить
напряжения по любой площадке, проходящей
через данную точку. Теперь уже мы
рассмотрим этот вопрос в случае, когда
исследуемая точка принадлежит растянутому
или сжатому стержню.
Пусть стержень
растянут силой F и в
поперечных сечениях стержня, как мы
знаем, возникают нормальные напряжения
равные
,
где
- площадь поперечного сечения.
Проведем через
исследуемую точку
произвольное сечение, положение которого
задается углом
между осью стержня и внешней нормалью
к сечению. Кроме того, проведем еще
поперечное сечение. Выделим с помощью
указанных сечений элемент и рассмотрим
равновесие данного элемента.
По наклонной
площадке действует полное напряжение
.
проектируя силы, действующие на элемент
на ось стержня, получаем
Разлагая
на нормальное
и касательное напряжение, получаем
Переходя к функциям
угла
имеем
Уравнения (5) дают
возможность вычислить напряжения по
любым площадкам, проходящим через данную
точку, т.е. определяют напряженное
состояние при растяжении и сжатии.
Очевидно, что касательные напряжения
обращаются в нуль по двум площадкам
(поперечное сечение) и
(продольное сечение). Площадки, по
которым касательные напряжения равны
нулю, называются главными площадками,
а нормальные напряжения, действующие
по ним, главными напряжениями.
Очевидно, что одно из главных напряжений, действующее в попе-
речном сечении - является максимальным по модулю, что обосновывает использование формулы (1), как основной расчетной формулы при растяжении, сжатии, а другое главное напряжение, действующее в продольных площадках рано нулю. Таким образом, продольные площадки свободны от напряжений.
Из второго уравнения
(5) видно, что максимальные касательные
напряжения возникают по площадкам,
наклоненным к оси на угол
,
и равняются по величине
Максимальные касательные напряжения являются причиной разру-
шения образцов из хрупких материалов, испытываемых на сжатие.