Основная система.

У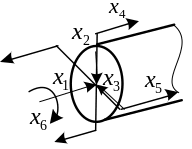 равнение метода сил выглядит также как и в плоском случае.

(1)

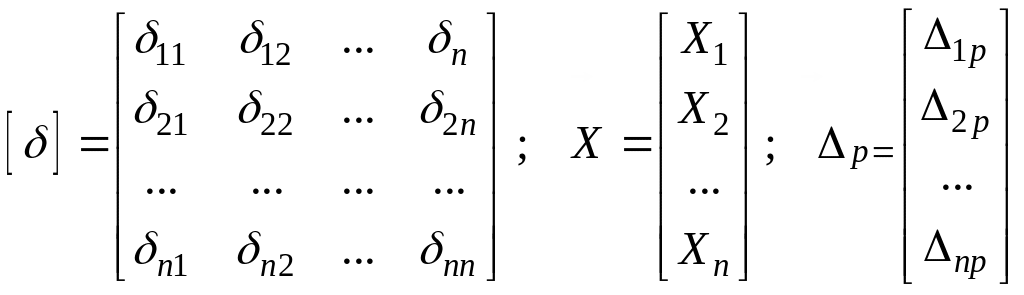Определяя единичные ( ) и грузовые ( ) перемещения мы учитываем не один внутренний силовой фактор, как в случае плоской системы, а три внутренних силовых фактора: два изгибающих момента и крутящий момент. Интегралы Мора для этого случая выглядят:

здесь - крутильная жесткость ( - для круглого сечения).

Плоскопространственные рамы.

П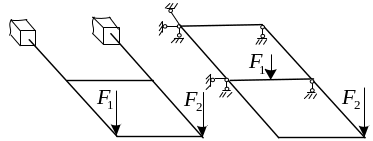 лоскопространственными рамами называются плоские рамы, нагруженные нагрузкой перпендикулярной плоскости рамы.

В поперечных сечениях плоскопространственных рам возникают 3 внутренних силовых фактора: изгибающий момент, соответствующая ему поперечная сила, крутящий момент.

Подставляя найденные главные напряжения в выражение для по различным теориям

1) Теория наибольших касательных напряжений

2) Теория энергии формоизменения

3) Теория Мора

Эти формулы можно использовать не только для изгиба, но и для расчета (сжатия) и изгиба с кручением.

В случае изгиба с кручением круглых валов, учитывая, что

П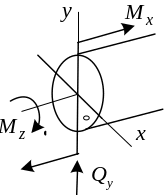 олучим

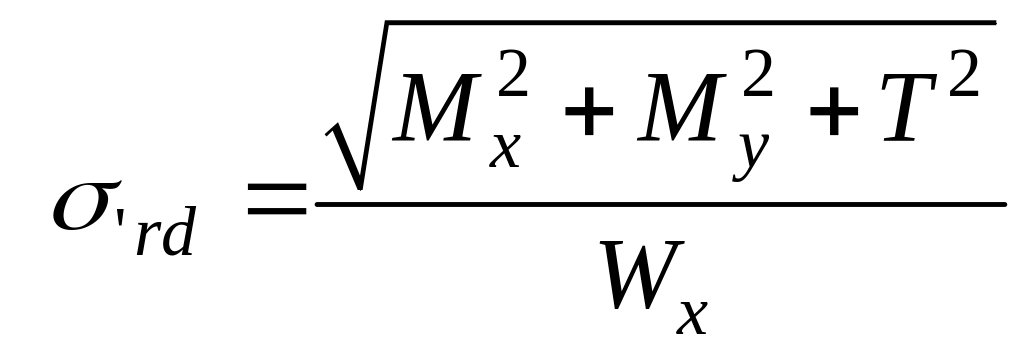
Коэффициенты и свободные члены уравнений метода сил определяются таким же образом как и для пространственных рам, но, естественно, выпадает член с одним из изгибающих моментов Пример:

Лекции XXIV Расчет осесимметричных оболочек по безмоментной теории.

Напомним, что оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми (толщина оболочки) есть величина малая по сравнению с остальными размерами.

Поверхность, равноудаленная от ограничивающих поверхностей называется срединной поверхностью оболочки.

Оболочки могут иметь переменную толщину, однако мы будем рассматривать только оболочки постоянной толщины.

Оболочки имеют весьма широкое распространение в технике: корпуса судов, летательных аппаратов и ракет; сосуды для хранения жидкостей и газов; трубы; детали машин и приборов; оболочки покрытия в строительстве и т.д.

Достоинством оболочек является то обстоятельство, что обладая выгодными упругими свойствами они способны выдерживать большие нагрузки при минимальной толщине. Это позволяет создавать конструкции легкие и прочные, незаменимые в тех случаях, когда малая масса конструкции жизненно необходима.

Рассмотрим тонкие оболочки, у которых толщина мала по сравнению с радиусом кривизны поверхности. Если допустить обычную для технических расчетов относительную погрешность в 5%, то тонкими оболочками можно считать такие оболочки, у которых ,

где h – толщина оболочки, R – радиус кривизны.

Приведенная граница, конечно, является условной и иногда,

теорией тонких оболочек пользуются для расчета более толстых оболочек, чем указано выше, допуская при этом большую погрешность.

Наиболее распространенный вариант теории тонких оболочек-

– это вариант, основанный на гипотезе Кирхгофа-Лява:

1) Элемент, прямолинейный и нормальный к срединной поверхности до деформации, остается прямолинейным и нормальным к деформированной срединной поверхности.

2) Нормальными напряжениями на площадках параллельных срединной поверхности можно пренебречь.

Эти допущения совешенно аналогичны тем, что приняты для балок (гипотеза плоских сечений), задача трехмерная сводится к задаче двухмерной. Аналогично тому, как при расчете балок исследование сводится к объекту одномерному – оси балки, так и при расчете тонких оболочек рассматривается объект двухмерный – срединная поверхность оболочки.

Мы будет рассматривать только один тип оболочек – осесиммет-ричные оболочки, т.е. оболочки вращения, срединная поверхность которых образуется вращением кривой относительно оси симметрии.

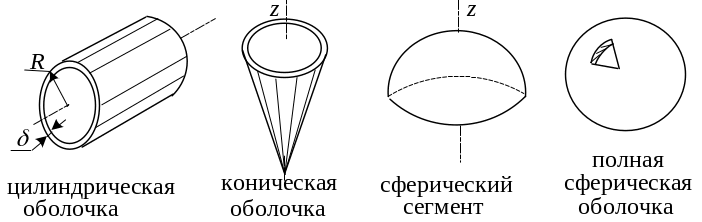
К осесимметричным оболочкам относятся наиболее распространен-

ные в практике цилиндрические, конические, сферические оболочки.

Ведя расчет оболочек, мы будем исходить из так называемой безмоментной теории. Т.е. считать, что нормальные напряжения распределяются по толщине оболочки равномерно.

У словия существования безмоментного напряженного состояния:

1) Поверхность оболочки должна быть плавной, так чтобы радиус кривизны не претерпевал резких изменений и не обращался в нуль.

2) Нагрузка, действующая на оболочку, должна также меняться плавно. Не должно быть сосредоточенных сил.

3) Условия закрепления краев оболочки должны быть таковы, чтобы на краях не возникали изгибающие моменты и поперечные силы.

Безмоментное напряженное состояние чрезвычайно выгодно, т.к. приводит к рациональному распределению напряжений и экономии материала.