Напряжение

М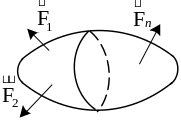 ерой внутренних сил, величиной характеризующей интенсивность их распределения является напряжение.

Рассмотрим тело, находящееся под действием системы уравновешенных сил. Будем исследовать внутренние силы в малой области, окружающей точку . Проведем через данную точку сечение некоторой поверхностью. Внешняя нормаль этой поверхности в точке - Отбросим часть, лежащую по правую сторону от сечения и заменим ее действие на оставшуюся часть внутренними силами. Выделим в окрестности точки площадку . Результирующая внутренних сил, действующих на площадке пусть равняется .

Д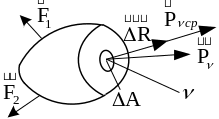 елим результирующую силу на , получаем величину среднего напряжения по площадке. . Величина зависит от размеров площадки.

Перейдем к пределу, стягивая площадку к точке

Величина - называется вектором напряжения в данной точке по площадке с внешней нормалью .

О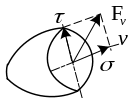 чевидно, что, выбирая другим образом ориентированную площадку, проходящую через данную точку, мы получаем другое значение вектора напряжения.

Совокупность всех векторов напряжения по площадкам, проходящих через данную точку, составляет напряженное состояние в данной точке.

Величину обычно раскладывают на две составляющие: нормальное напряжение , направленное по внешней нормали к площадке и касательное напряжение , лежащее в плоскости площадки.

Перемещения и деформации.

Р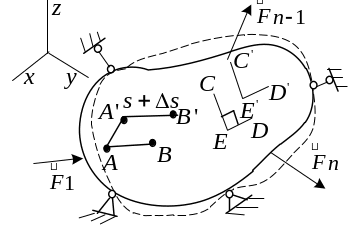 ассмотрим тело, имеющее такое количество связей, что движение его как жесткого тела исключено. Перемещения точек тела обусловле-ны деформативностью материала.

Пусть под действием сил тело деформировалось, и точка перешла в новое положение . Тогда вектор называется вектором перемещения, а его проекции на координатные оси обозначены соответственно

З ададим в точке некоторое направление и пусть длина отрезка В деформированном состоянии длина отрезка изменилась и стала равной Тогда величину

называют линейной деформацией в данной точке по направлению . Пусть угол между отрезками и – прямой.

После деформации тела величина угла изменится.

Величина называется угловой деформацией или углом сдвига.

Уже сейчас отметим, что между напря-

жениями и деформациями существует связь и эта связь принципиаль-

но может быть установлена только экспериментальным путем.

Принципы сопротивления материалов

Таких принципов (основных правил) три.

1. Принцип неизменности начальных размеров.

Будем считать, что перемещения, возникающие в системах, малы по сравнению с их размерами.

Так, например, определяя изгибающий момент в балке, мы не

у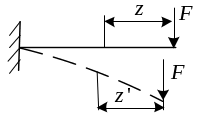 читываем того обстоятельства, что в результате изгиба балки плечо у силы изменится.

2. Принцип независимости действия сил.

Если на систему действуют несколько сил, то напряжения (перемещения, деформации, внутренние силовые факторы), возникающие от совместного действия этих сил, можно определить следующим образом: определить от действия каждой из сил порознь и результаты сложить.

Справедливость этого принципа вытекает из принятия изложенно-

го выше принципа неизменности начальных размеров и допущения, что между напряжениями и деформациями существует связь, определяемая простейшим законом – законом линейной упругости (закон Гука). В этом случае поведение наших конструкций будет описываться математически линейными системами, с этой точки зрения принцип независимости действия сил есть не что иное, как хорошо знакомый принцип суперпозиции.