Применение различных теорий предельного напряженного состояния.
Прежде всего,
следует заметить, что все упомянутые
теории дают неплохие результаты для
смешанных напряженных состояний, когда
имеют разные знаки. Использование этих,
как прочем, и других теорий в случае
глубокого всестороннего сжатия и
растяжения сомнительно.
Теория наибольших касательных напряжений и энергии формоизменения применимы для материалов совершенно пластичных одинаково работающих на растяжение и сжатие. Теория Мора применима и к материалам хрупко-пластическим, не обладающими свойством пластичности в большей мере и лучше работающим на сжатие чем на растяжение. Теория Мора заслуживает предпочтения из-за того, что она основана на экспериментальном описании явления.
Теории разрушения.
Явление разрушения
более сложно и менее изучено, чем переход
в пластическое состояние. В дальнейшем
будут изложены некоторые элементарные
сведения из бурно развивающейся отрасли
“Механики разрушения”. Сейчас же
заметим, что при отсутствии других
данных возможна оценка коэффициента
запаса по разрушению с помощью теории
Мора
где
и
-
пределы прочности при растяжении и
сжатии.
ЛЕКЦИИ XXII
Изгиб с кручением.
Расчетные формулы по различным теориям предельного напряженного состояния.
О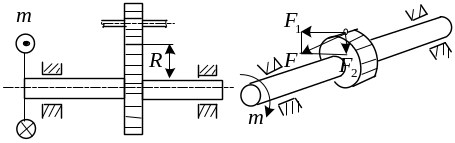
дним
из наиболее частых нагружений в
машиностроительной практике является
со-вместное воздействие изгиба и
кручения. В таких условиях например
работают валы редукторов. Приводя силы,
действующие на вал к оси вала, имеем
следующую расчетную схему.
Н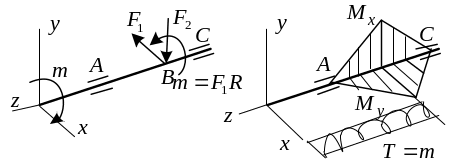
а
участке АВ вал будет работать на изгиб
с кручением. Очевидно, что наиболее
опасным будет сечение В. Наибольшие
нормальные напряжения, возникающие в
этом сечении
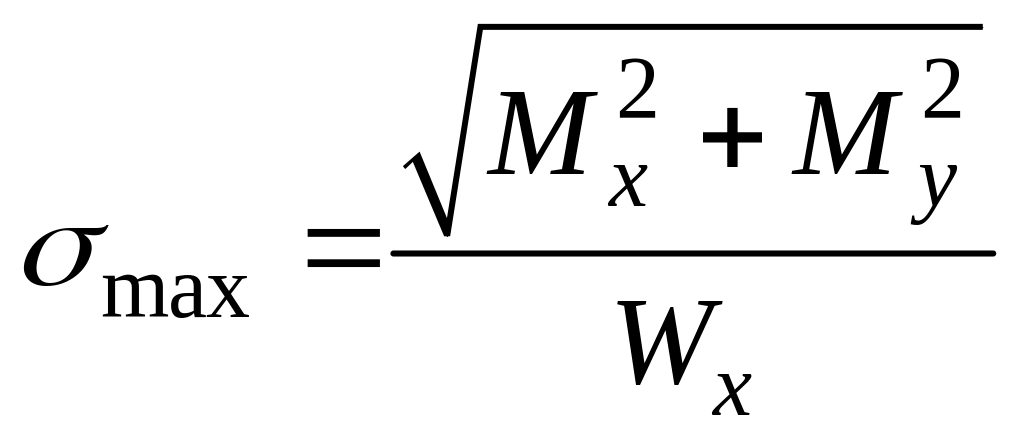
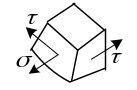
Наибольшие касательные напряжения
В наиболее опасной точке будет возникать плоское
напряженное
состояние
В качестве примера мы рассматривали круглое напряженное состояние, но такой же характер напряженного состояния будет при любом поперечном сечении и последующие результаты применимы для произвольных сечений.
Найдем главные напряжения
;
Подставляя найденные главные напряжения в выражения для по различным теориям
1. Теория наибольших
касательных напряжений
2. Теория энергии
формоизменения
3. Теория Мора
Эти формулы можно использовать не только для изгиба, но и для растяжения (сжатия), изгиба и кручения.
В случае изгиба с кручением круглых валов, учитывая, что
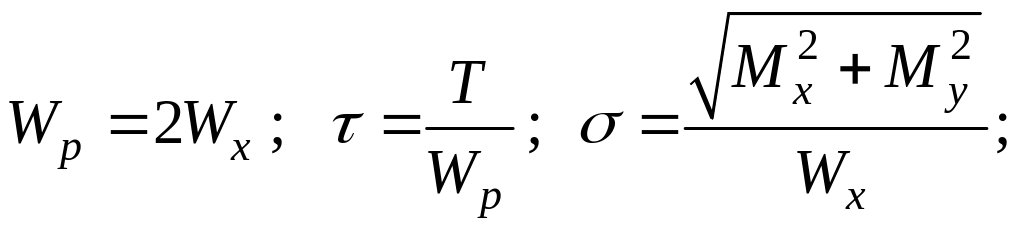получим
Пример.
Лекции XXIII Расчет пространственных и плоскопространственных рам
Р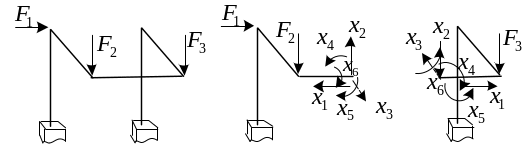
асчет
пространственных статически неопределимых
рам принципиально не отличается от
расчета плоских рам. Основная система
также выбирается путем отбрасывания
лишних связей: удаления опорных
закреплений или разрезания стержней
либо того и другого.
Например:
показанная на рисунке рама 6 раз статически неопределима. Основную систему можно выбрать, введя разрез. Основными неизвестными будут внутренние силовые факторы в месте разреза.