Лекции XIX Классификация напряженных состояний

Частные случаи определения главных напряжений

а) Если все три главных напряжения отличны от нуля, то напряженное состояние называется объемным или трехосным.

б) Когда два главных напряжения отличны от нуля напряженное состояние называется плоским или двуосным. Кубичный инвариант при этом равен нулю: .

В этом случае уравнение принимает вид;

Откуда следует, что один из корней равен нулю. Два остальных найдутся из решения квадратного уравнения

Если напряжения действуют только лишь в одной плоскости, например, в плоскости, параллельной координатной плоскости , то тензор напряжений будет состоять из трех независимых компонентов (нулевых).

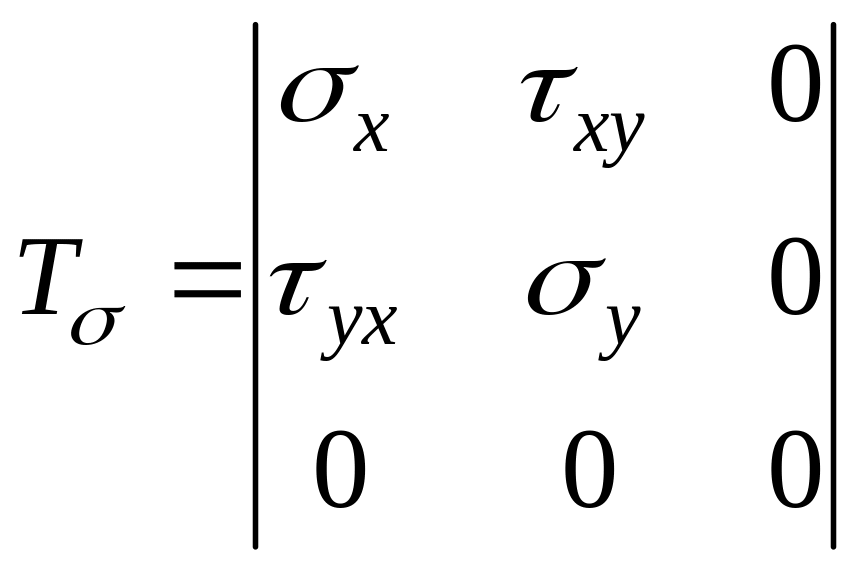
Варианты напряженного состояния будут равны:

; Подставим это выражение в (11).

Получаем главные напряжения:

в) Если кубичный и квадратичный инварианты одновременно равны нулю, то уравнение (3) дает лишь один корень отличный от нуля.

Напряженное состояние называется в это случае линейным или одноосным.

Приведенная выше классификация не является исчерпывающей, и поэтому принято классифицировать напряженное состояние еще в зависимости от знака главных напряжений. В этом случае все напряженные состояния можно разделить на три класса:

1. Трехосные растяжения. В этом случае ни одно из главных напряжений не является сжимающим.

2. Трехосные сжатия. В этом случае ни одно из главных напряжений не является растягивающим.

3. Смешанное напряженное состояние, когда наибольшее и наимень-

шее главные напряжения имеют разные знаки.

Примеры различных типов напряженных состояний см. учебник В.И. Феодосьев “Сопротивление материалов”.

ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПЛОЩАДКАМ ПАРАЛЛЕЛЬНЫМ НАПРАВЛЕНИЮ ОДНОГО ИЗ ГЛАВНЫХ НАПРЯЖЕНИЙ

В практических задачах часто сталкиваются с таким положением, когда положение одной из главных площадок заранее известно. Решение в этом случае значительно упрощается.

Р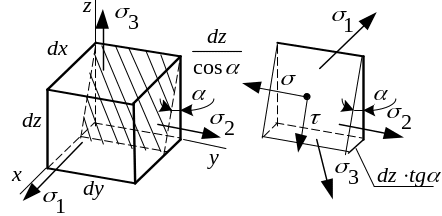 ассмотрим элемент в виде параллелепипеда. Грани параллелепипеда являются главными площадками. Смотреть рисунок.

Выделим из параллелепипеда треугольную призму. Наклонная к координатным плоскостям грань параллельна направлению главного напряжения . Составим условие равновесия элементарной призмы.

Проектируя на нормали к площадке, получаем:

Сумма проекций всех сил на направление даст:

Упрощая полученные выражения получаем окончательно:

(12)

Если рассматривать и как декартовы координаты на плоскости, то легко обнаружить, что уравнения (12) представляют собой уравнения окружности в параметрическом виде:

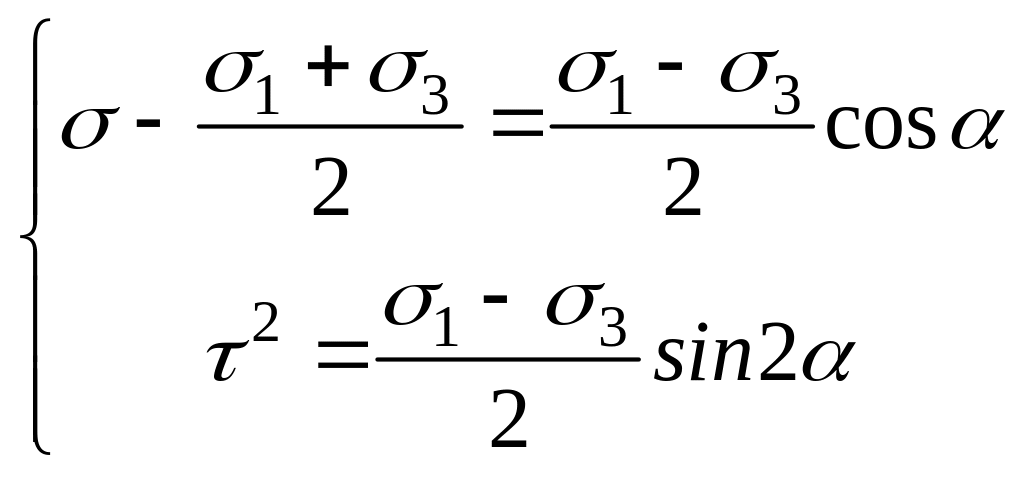
Возводя оба равенства в квадрат и складывая получаем:

, т. е.

уравнение окружности с центром, находящимся на оси на расстоянии от начала координат и радиусом . См. рисунок.

П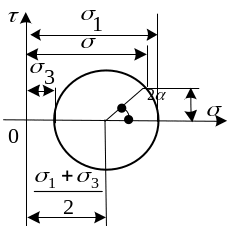 олученный круг называется круговой диаграммой Мора. Если не принимать во внимание знак касательного напряжения, то можно ограничиться построением только верхней половины круга Мора.

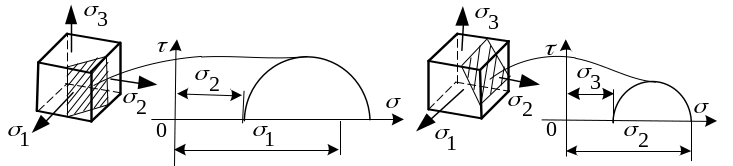
Построенная диаграмма имеет следующий смысл: каждой площадке параллельной направлению напряжения соответствует точка на окружности.

Можно построить круговые диаграммы и для площадок параллельных направлению главных напряжений и . См. рисунок.

Площадкам общего положения, не параллельным ни одному из главных напряжений, соответствуют точки расположенные в заштрихованной области.

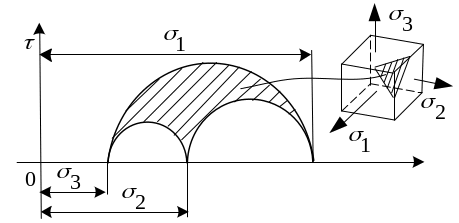
Наложим круговые диаграммы на один чертеж

О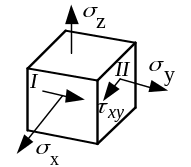 пределение главных напряжений в случае, когда известно положение одной из главных осей.

Пускай - главное напряжение. Требуется найти величину двух других главных напряжений.

Введем систему координат и нанесем точки, соответствующие площадкам и . См. рисунок

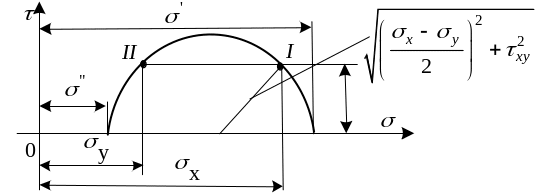
Проведем через точки и окружность, центр которой лежит на оси . Точки пересечения круговой диаграммы с осью дадут значения главных напряжений и .

Определяя и из чертежа, приходим к знакомой формуле (12).