Лекция XIII Упруго-пластический изгиб. Чистый упруго пластический изгиб.

Рассмотрим стержень, работающий в условиях чистого изгиба. Пусть поперечное сечение стержня имеет две оси симметрии и .

Б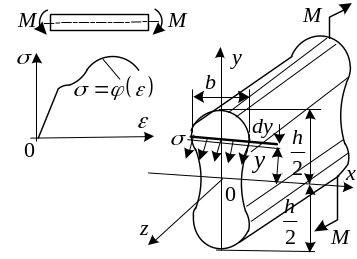 удем считать, что материал одинаково работает как на растяжение, так и на сжатие и нам задан закон, связывающий напряжения с дефор-мацией: В основу решения положена гипотеза плоских сечений (см. лекция 6) или обозначим кривизну

Форма поперечного сечения балки задается шириной: где вместо аргумента можно ввести безразмерную координату и рассматривать функцию .

Момент внутренних сил, действующих на элементарную площадку шириной и высотой (см. рис.) равняется:

Изгибающий момент в сечении (учитывая, что ось -ось симметрии):

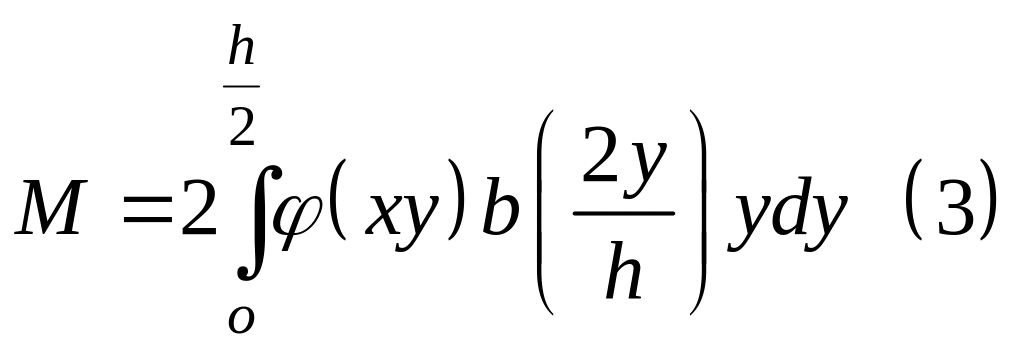
Выражение (3) можно преобразовать, заменив переменную интег-

тегрирования на величину ей пропорциональную . Наибольшие деформации возникнут в точке наиболее удаленной от

оси при ;

Интеграл может быть найден при простом

законе и аналитически, а в более сложных случаях чис-

ленно.

Т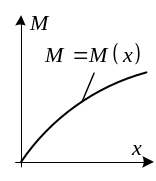 аким образом, по заданной кривизне балки мы можем найти величину изгибающего момента. Задаваясь различными значениями кривизны , мы можем с помощью (4) найти соответствующие им значения изгибающего момента и построить график зависимости от .

Имея этот график, можно по заданному моменту найти величину , затем деформации по формуле , а по деформациям из закона опреде-

лить напряжения, возникающие в поперечном сечении балки при заданном моменте.

Изгиб стержня прямоугольного сечения при идеальном упруго-пластичном материале

Пусть материал следует диаграмме идеального упругопластического материала. Связь между напряжениями и деформациями в этом случае выглядит:

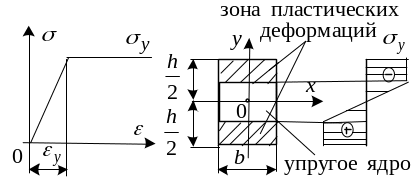1. п ри

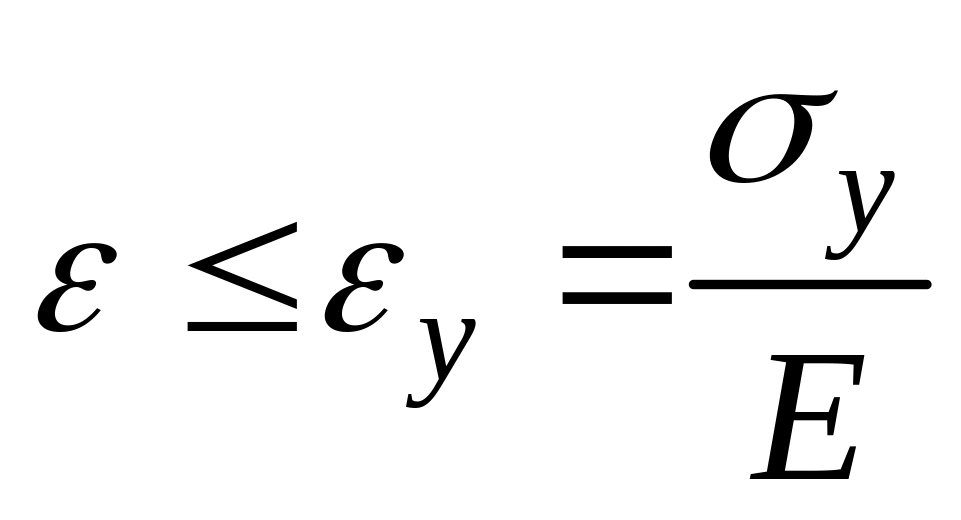
(закон Гука)

2) при

Подставим эти выражения в интеграл (5)

учтем, что тогда подставим в (4)

Напомним, что ,тогда (6) можно выразить:

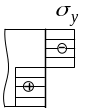. Решим (7) относительно кривизны 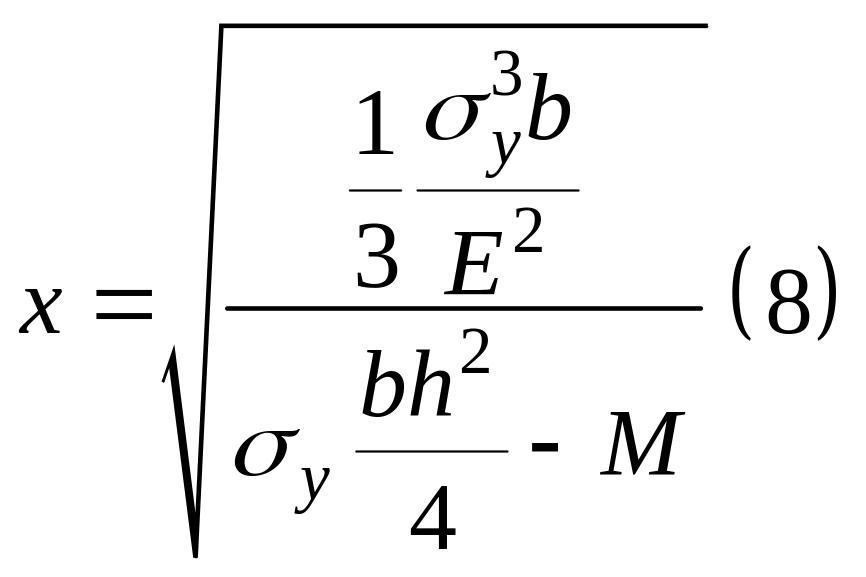Анализируя (7), мы видим, что наибольшее значение момента не превышает величины: , которую назовем предельным моментом. Это значение соответствует полному переходу сечения в пластическое состояние.

Однако, для того чтобы момент достиг предельного значения, как

показывает (8) кривизна должна обратиться в бесконечность, что конечно невозможно. Таким образом, величина в действительности не может быть достигнута.

Величина называется пластическим моментом сопротив-

ления (сравним с моментом сопротивления .

Разумеется, что формула (8), выведенная в предположении, что балка работает в упруго-пластической стадии, неприменима при малых значениях момента, соответствующих упругой работе.

в (8) должно находиться в пределах

Определение остаточных напряжений при упруго пластичном изгибе

Загружая балку таким образом, чтобы она работала в упруго пластичной стадии, а затем разгружая, мы обнаруживаем в ней остаточные напряжения, которую можно найти по закону упругой разгрузки (лекция 4). Напомним: для того, чтобы найти остаточные напряжения

Н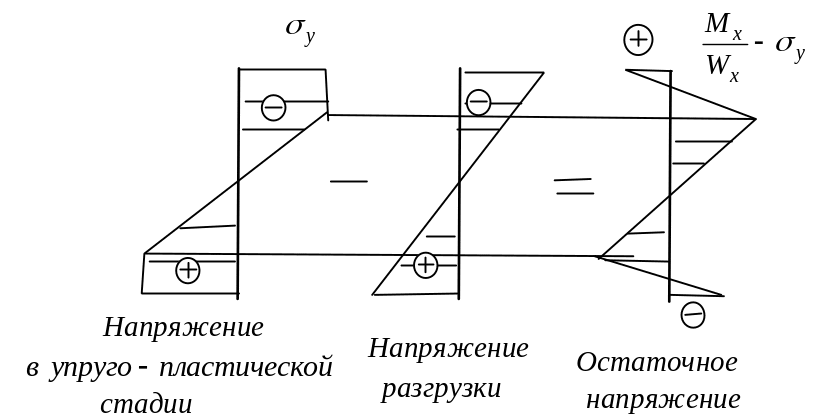 ужно из фактического напряжения вычесть напряжения, полученные в предположении, что система работает упруго.

Остаточные напряжения представляют собой самоу-равновешенную систему, т. е.

систему внутренних сил статически эквивалентную нулю.