Метод сил.
Изложение теории будем сопровождать примером расчета рамы. Расчет статически неопределимых систем по методу сил начинается с выбора основной системы.
Определение Основной системой называется система статически определимая, кинематически неизменяемая, полученная из данной путем отбрасывания лишних связей.
Замечание 1. Отбрасывание связей осуществляется либо путем отбрасывания опорных стержней, либо путем введения разрезов стержней
Замечание 2. Нельзя выбирать в качестве основной системы мгновенно изменяемые системы.
Согласно аксиоме
связей, отбросив связи, мы должны заменить
их действия реакциями: реакциями
отброшенных опорных закреплений,
внутренними силовыми факторами в местах
разрезов. Эти реакции отброшенных связей
называются обычно основными неизвестными
(
).
Основная система, нагруженная помимо заданных сил основными неизвестными, называется эквивалентной системой.
Пример: Построить эпюру моментов для данной статически не-
о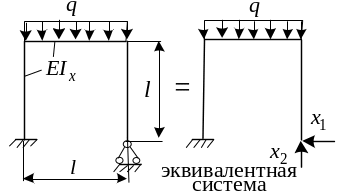
пределимой
рамы.
Таким образом, расчет сложной статически неопределимой системы заменяется расчетом более простой статически определимой, но часть нагрузки при этом (основные неизвестные) нам известна. Для того, чтобы найти основные неизвестные надо составить условия эквивалентности исходной системы и основной системы, загруженной помимо заданной нагрузки основными неизвестными. Эти условия обычно записываются в форме канонических уравнений метода сил
где:
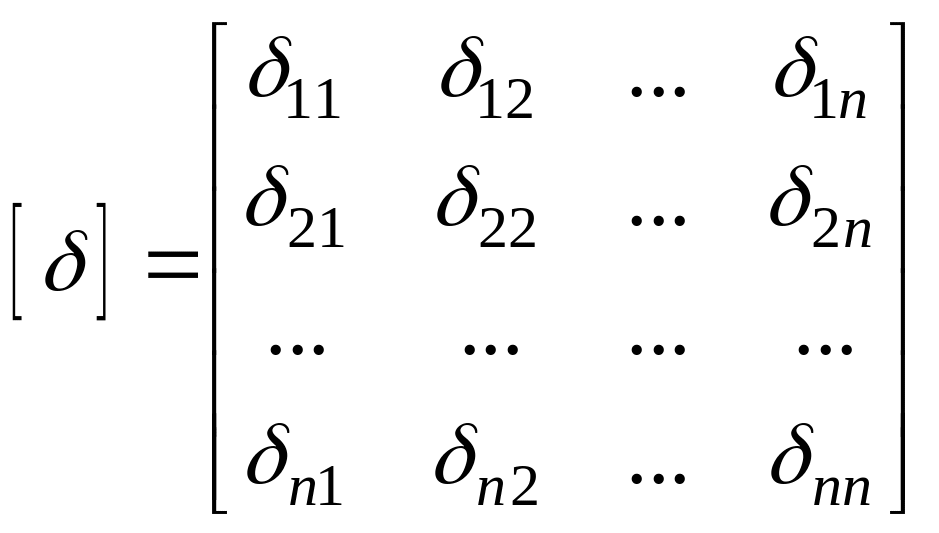матрица
единичных перемещений или
или
- изгибающие моменты
в основной системе соответственно от
сил
- соответственно
площадь эпюры моментов и ордината под
центром тяжести при вычислении интеграла
Мора по правилу Вере-
щагина.
Т.е. - перемещение по направлению силы , вызванное силой .
По теореме о
взаимности перемещений
при
т.е. матрица
симметрична.
При
.
Эти коэффициенты, стоящие на главной
диагонали матрицы, называют обычно
главными, а остальные – побочными.
-
-
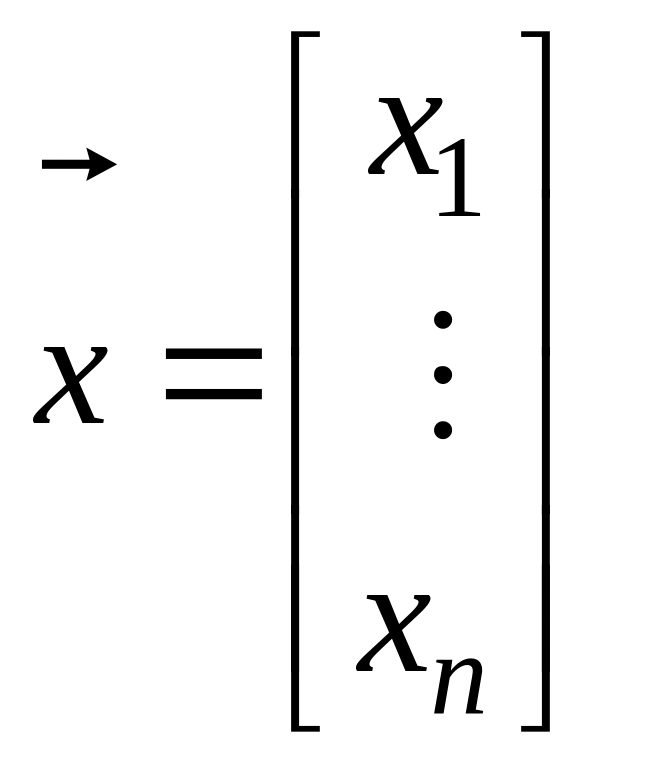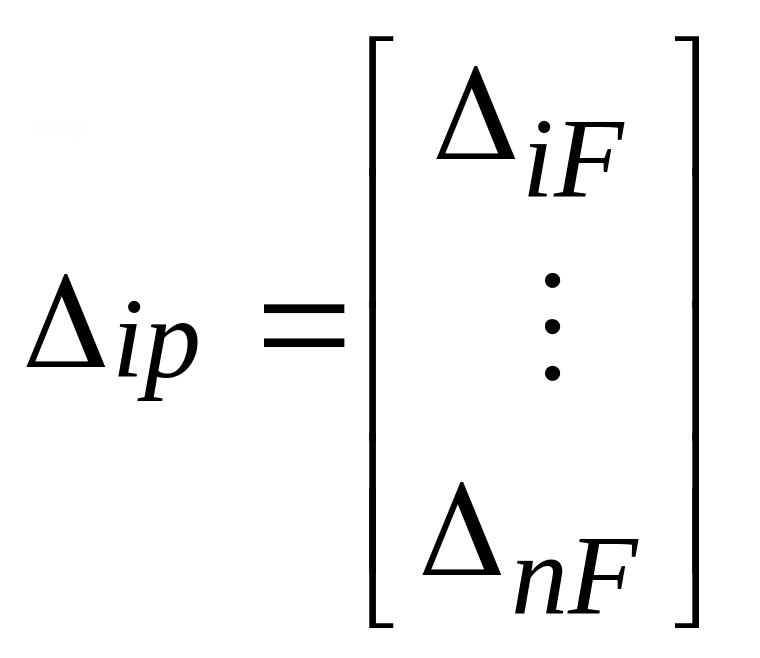или
- изгибающий момент от заданной нагрузки.
-
перемещение по направлению силы
,
вызванное заданной нагрузкой.
Если записать
уравнения (1) в обычной форме, то они
будут выглядеть
(1а)
Разберемся в смысле записанных уравнений. Рассмотрим 1-е из них:
- перемещение по
направлению силы
,
вызванное ее же самой,
-перемещение
в том же направлении, вызванное силой
-
перемещение в направлении силы
,
вызванное заданными си-
лами.
Таким образом, каждое из канонических уравнений метода сил можно трактовать как условие равенства нулю перемещения по направлению отброшенной связи (связь то на самом деле есть и она не допускает перемещений в своем направлении).
Для того, чтобы определить коэффициенты в свободные члены системы (1) надо к основной системе приложить единичные силы по направлению основных неизвестных (прикладывая каждую силу порознь), построить единичные эпюры, затем построить эпюру в основной системе от заданных сил. Перемножая полученные эпюры по правилу Верещагина, находим основные неизвестные. Система канонических уравнений в рассматриваемом примере:
Построим единичные и грузовые эпюры.
Перемножим эпюры по правилу Верещагина.
Экстремум эпюры моментов найдем из суммарной эпюры.