Теорема о взаимности работ (теорема Бетти).

Работа первой силы на перемещении ее точки приложения, вызванном второй силой равняется работе второй силы на перемещении ее точки приложения, вызванном первой силой.

Будем считать, что система консервативна и работа в ней не зависит от промежуточных состояний, а зависит лишь от начального и конечного состояния системы.

(Линейно-упругие системы всегда консервативны, если загружены консервативными силами, т.е. силами, имеющими потенциал).

В качестве модели системы выберем консольную балку.

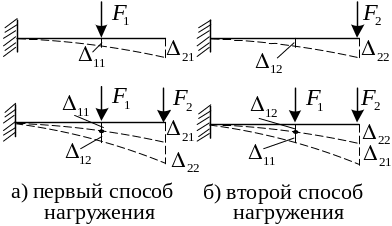Перемещения будем обозначать:

- перемещение по направлению силы , вызванное силой .

Нагрузим систему вначале силой , а затем приложим силу .

Работа сил, приложенных к системе запишется:

(Почему два первых члена имеют множитель 1/2, а последний нет?)

Затем первой приложим силу а второй - .

Т.к. система консервативна, а также потому, что начальные и конечные состояния в обоих случаях совпадают, то работы необходимо равны, откуда следует . Если положить ,

то получим частный случай теоремы Бетти – теорему о взаимности

перемещений.

Перемещения, вызванные единичными силами, мы будем обозна-

чать (смысл индексов прежний). Тогда

Потенциальная энергия деформации плоской стержневой системы.

Будем рассматривать плоскую систему, т.е. систему все стержни которой и все силы лежат в одной плоскости. В стержнях такой системы в общем случае могут возникать при внутренних силовых факторах:

Упругая система деформируясь накапливает при этом энергию (упругую энергию) называемую потенциальной энергией деформации.

а) Потенциальная энергия деформации при растяжении и сжатии.

П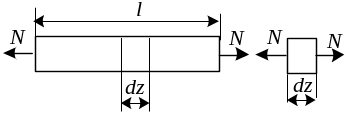 отенциальная энергия накопленная в малом элементе длиной dz будет равняться работе сил приложенных к этому элементу

Потенциальная энергия для стержня:

Замечание. и - необязательно постоянные величины.

б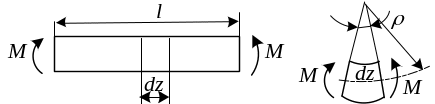 ) Потенциальная энергия при изгибе.

Для стержня:

в) Поперечные силы вызывают сдвиги, и им соответствует потен-

циальная энергия сдвига. Однако, эта энергия в большинстве случаев невелика и мы не будем ее учитывать.

Замечание. В качестве рассматриваемых объектов у нас фигурировали прямые стержни, но полученные результаты применимы и криволинейным стержням малой кривизны, у которых радиус кривизны приблизительно в 5 раз и более превосходит высоту сечения.

Потенциальная энергия для стержневой системы может быть запи-

cана:

Здесь учтено то обстоятельство, что при растяжении и сжатии сечения не поворачиваются, следовательно, изгибающие моменты при этом работы не совершают, а при изгибе не меняется расстояние по оси между смежными сечениями и работа нормальных сил равна нулю. Т.е. потенциальную энергию изгиба и растяжения – сжатия можно вычислить независимо.

Знаки стимулирования означают, что потенциальная энергия вычисляется для всей системы.

Теорема Кастельяно.

Выражение (3) показывает, что потенциальная энергия деформации является однородной квадратичной функцией и , а те в свою очередь линейно зависят от сил, действующих на систему таким образом является квадратичной функцией сил.

Теорема. Частная производная от потенциальной энергии по силе равняется перемещению точки приложения этой силы по направлению последней. Доказательство:

Пусть - потенциальная энергия, соответствующая силам системы Рассмотрим два случая.

1) Вначале приложены все силы а затем одна из них получает малое приращение тогда полная потенциальная энергия равна:

2) Вначале приложена сила а затем прикладываются силы

В этом случае потенциальная энергия равна:

Т.к. начальное и конечное состояние в обоих случаях одинаково, а система консервативна, то потенциальные энергии надо приравнять

Отбрасывая малые второго порядка, получаем