Министерство образования и науки Российской Федерации

Калужский филиал государственного образовательного учреждения высшего профессионального образования

«Московский государственный технический университет

имени Н.Э. Баумана»

(КФ МГТУ им. Н.Э. Баумана)

Кафедра К5-КФ «Сопротивления материалов»

ЛЕКЦИИ

по

“CОПРОТИВЛЕНИЮ МАТЕРИАЛОВ”

2011г

МОДУЛЬ I

Лекция I Основные понятия и допущения сопротивления материалов

Части машин и инженерных сооружений в процессе эксплуатации подвергаются воздействию сил самой различной природы. Тела, выполненные из реальных материалов, под действием сил изменяют свои размеры и форму – деформируются. При достаточно больших значениях сил конструкция может разрушиться, т.е. распасться на части, либо получить такие деформации, что ее эксплуатация станет невозможной. Проектируя конструкцию, инженер должен назначить ее размеры таким образом, чтобы гарантировать ее неразрушимость и ограничить деформации, т.е. он должен обеспечить ее прочность и жесткость, Простейшие, но вместе с тем наиболее типичные задачи подобного рода решаются в курсе “Сопротивления материалов”.

Сопротивление материалов – учебная дисциплина, занимающаяся расчетом частей машин и инженерных сооружений на прочность и жесткость. Приведенное определение является приблизительным и условным, но об этом речь впереди.

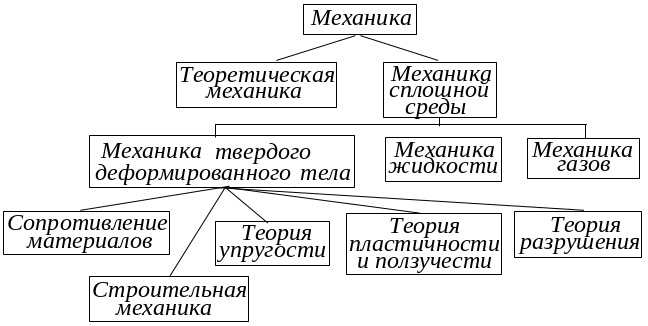
Сопротивление материалов является частью механически твердого деформируемого тела и место данной дисциплины можно условно определить следующим образом:

Традиционный курс сопротивления материалов в настоящее время уже не удовлетворяет современного инженера и в курсе сопротивления материалов начинают проникать методы теории упругости, теории пластичности механики разрушения. Подобная тенденция отразится и на нашем курсе.

Понятие расчетной схемы конструкции.

В сопротивлении материалов анализ реального объекта (детали,

ли, конструкции) подменяется анализом расчетной схемы.

Расчетная схема – абстрактная модель реального объекта, от

ражающая основные характерные особенности последнего.

Схематизация осуществляется по 3 направлениям:

1. Схематизация свойств материала.

2. Схематизация геометрической формы конструкции.

3. Схематизация сил, действующих на конструкцию.

Остановимся на этом несколько подробнее.

1. Схематизация свойств материалов

а ) Гипотеза сплошного однородного тела - состоит в том, что реальное тело, состоящее из атомов и молекул, заменяется гипотетическим сплошным однородным телом. Тело или среда называется спло-шной, если любой выделенный малый объем содержит вещество. Однородность означает, что свойства тела во всех точках одинаковы. На-иболее распространенные в технике материалы – неоднородны, они имеют зачастую (напр. металлы) кристаллическое строение и свойства элементов по разному выделенных из кристаллов различны. Однако. размеры кристаллических зерен пренебрежимо малы по сравнению с размерами деталей, и, в результате интересующие нас тела обладают свойством относительной однородности.

Гипотеза сплошного однородного тела позволяет рассматривать интересующие нас величины, как непрерывные функции координат и использовать аппарат математического анализа.

б) В зависимости от поведения при нагружении различают тела упругие и пластические.

Упругие тела характеризуются однозначной зависимостью

между силами и деформациями. После снятия нагрузки деформации исчезают полностью.

У пластических тел деформации зависят не только от величины, но и от истории нагружения. После снятия нагрузки тело в первоначальное состояние не приходит. Появляются остаточные деформации.

Свойства упругости и пластичности относительны, так, например, стальная пружина, будучи сжата небольшой силой, ведет себя как упругая система, а будучи сжата большой силой, получает остаточные деформации. Это говорит о том, что для стали малые деформации упруги, а большие - пластические.

В большей части курса мы будем приписывать материалу упругие свойства.

в) В рассматриваемых вопросах будем считать тела изотропными,

т.е. обладающими одинаковыми свойствами во всех направлениях.

Тела, не обладающие таким свойством, называются анизотропными.

Кристалл, например, всегда анизотропен. Определяется расположением атомов в кристаллической решетке. Однако, технические сплавы состоят из кристаллических зерен, ориентация которых беспорядочна, поэтому в теле, содержащем большое количество кристаллических зерен нельзя выделить какое-то предпочтительное направление. Таким образом, подобные тела можно считать изотропными.

В прокатанном металле зерна деформируются в направлении прокатки, и в результате материал становится анизотропен, однако подобная анизотропия обычно невелика и не учитывается в расчетах.

Существуют конструктивно анизотропные материалы (армированные пластики, фанера, железобетон).

1. Схематизация геометрической формы

По принципу пространственной протяженности расчетные схемы классифицируются следующим образом:

а) Массивные конструкции – тела, у которых все три размера есть величины одного порядка (подшипники, толстостенные трубы, фундаменты под оборудование),

б) Тонкостенные конструкции: пластинки и оболочки. В этом случае два размера велики по сравнению с третьим - толщиной.

Подобную расчетную схему имеют сосуды для жидкостей и газов, корпуса судов и летательных аппаратов, конструкции бункеров, перекрытия и покрытия зданий, тонкостенные трубы, у которых дли-

на сопоставима с поперечными размерами, мембраны приборов и т.д.

в ) Стержни или брусья. Тела, у которых один размер – длина велик по сравнению с двумя другими размерами. Стержень характеризуется осью – некоторой кривой или прямой и поперечным сечением. Поперечное сечение перпендикулярно к оси и его центр тяжести лежит на оси.

Стержни являются основным объектом изучения сопротивления материалов.

г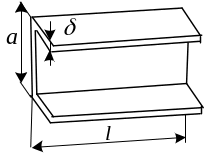 ) Тонкостенные стержни. Тела, у которых толщина поперечного сечения значительно меньше характерного размера поперечного сечения, который в свою очередь значительно меньше длины.

Подобный тип расчетной схемы имеют, например, стержни, выполненные из прокатных профилей: