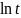- •Лекция 1
- •Множество точек на плоскости.
- •1.2 Задачи, приводящие к понятию двойного интеграла.
- •Определение двойного интеграла.
- •Геометрический и механический смысл двойного интеграла.
- •Свойства двойного интеграла.
- •Лекция 2
- •2.1. Вычисление двойного интеграла в декартовой системе координат
- •2.2. Вычисление двойного интеграла в полярной системе координат.
- •2.3 Применение двойных интегралов
- •Лекция 3
- •3.1 Задачи, приводящие к понятию криволинейного интеграла.
- •3.2 Определение криволинейного интеграла.
- •Лекция 4
- •4.1 Формула Грина.
- •4.2 Условия независимости криволинейного интеграла от пути интегрирования на плоскости.
- •4.3 Вычисление криволинейного интеграла, который не зависит от пути интегрирования.
- •4.4 Условия независимости криволинейного интеграла от пути интегрирования в пространстве.
- •Лекция 5
- •5.1 Определение ряда. Определение сходимости ряда. Примеры.
- •5.2 Необходимый признак сходимости.
- •5.3 Действие над рядами.
- •5.4 Знакоположительные ряды. Теоремы сравнения.
- •Лекция 6.
- •6.1 Признак Даламбера.
- •6.2. Признак Коши.
- •6.3.Интегральный признак Коши.
- •Лекция 7
- •7.1 Знакочередующиеся ряды. Теорема Лейбница.
- •7.2. Оценка суммы знакочередующегося ряда
- •7.3 Ряды с произвольными членами. Абсолютная и условная сходимость ряда. Теорема о связи между абсолютной сходимостью и сходимостью ряда.
- •Лекция 8
- •8.1 Степенные ряды. Теорема Абеля
- •8.2 Интервал сходимости степенного ряда и его нахождение.
- •Лекция 9
- •9.1. Достаточные условия разложения функции в степенной ряд.
- •9.2. Применение степенных рядов.
- •Лекция 10
- •10.1. Ряды с комплексными членами.
- •10.2. Абсолютная и условная сходимость рядов.
- •10.3. Степенные ряды с комплексными членами. Теорема Абеля. Нахождение круга сходимости степенного ряда.
- •10.4. Нахождение круга сходимости степенного ряда.
- •10.5. Определение функций Формулы Эйлера.
- •Лекция 11
- •11.1.Комплексные числа в алгебраической и тригонометрической форме и действия над ними.
- •11.2. Действия над комплексными числами в алгебраической форме.
- •Тригонометрическая форма комплексного числа.
- •Функции комплексного переменного.
- •Предел, непрерывность, производная функции комплексного переменного.
- •Лекция 12
- •12.1. Интегрирование функций комплексного переменного.
- •12.2. Вычисление интеграла от функции комплексного переменного.
- •12.3. Основные свойства интеграла функции комплексного переменного
- •12.5. Интеграл Коши
- •12.6. Особые точки. Вычеты.
- •Лекция 13
- •13.1 Преобразование Лапласа.
- •13.2 Решение обыкновенных дифуравнений с постоянными коэффициентами.
- •Лекция 14
- •Лекция 15
- •15.1 Ряды Фурье для 2 периодической функции.
- •Лекция 16
- •16.1 Разложение 2 ɩ периодических функций в ряд Фурье.
12.5. Интеграл Коши
Пусть G есть односвязная область, ограниченная кусочно-гладкой кривой Г, а является аналитической в Ḡ. Это означает, что является аналитической в некоторой области G’ содержащей G.
Ф ормула
Коши связывает значение функции во
всякой внтутренней точке z
области G
со значениями данной функции на границе
области G.
Это означает, что значение аналитической
функции на Г вполне определяют значения
этой функции в области G.
ормула
Коши связывает значение функции во
всякой внтутренней точке z
области G
со значениями данной функции на границе
области G.
Это означает, что значение аналитической
функции на Г вполне определяют значения
этой функции в области G.
Формула Коши имеет вид:

Доказательство формулы Коши.
Рассмотрим
произвольную точку
 и функцию
и функцию
 Функция
Функция
 является аналитической в области Ḡ,
кроме точки
является аналитической в области Ḡ,
кроме точки
 .
Рассмотрим окружность γ
с центром в точке z
произвольно малого радиуса
такую, что γ
лежит внутри G.
Функция
будет аналитической во всех точках,
лежащих между контурами Г и γ,
включая сами контуры. Можно доказать,
что
.
Рассмотрим окружность γ
с центром в точке z
произвольно малого радиуса
такую, что γ
лежит внутри G.
Функция
будет аналитической во всех точках,
лежащих между контурами Г и γ,
включая сами контуры. Можно доказать,
что
 (5)
(5)
Последнее
равенство показывает, что
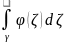 не зависит от радиуса γ
и является постоянным числом, равным
не зависит от радиуса γ
и является постоянным числом, равным
 .
Функция
стремится к определенному конечному
пределу при
.
Функция
стремится к определенному конечному
пределу при
 .
Имеем:
.
Имеем:

Если
положить
 становится
непрерывной в Ḡ,
т.е.
становится
непрерывной в Ḡ,
т.е.
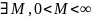 ,
такое, что
,
такое, что
 .
Учитывая
последнее неравенство, будем иметь:
.
Учитывая
последнее неравенство, будем иметь:
 ,откуда
следует, что
,откуда
следует, что
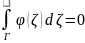 ,
т.к.
,
т.к.
 можно взять сколь угодно малым, т.е.
можно взять сколь угодно малым, т.е.

Но

12.6. Особые точки. Вычеты.
Определение
1.
Точка
называется
изолированной особой точкой однозначной
функции
,
если существует окрестность
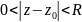 точки
(с исключенной точкой
),
в которой
аналитична.
точки
(с исключенной точкой
),
в которой
аналитична.
Различают три типа изолированных особых точек в зависимости от поведения функции в их окрестности:
Точка называется устранимой особой точкой, если существует конечный предел

Точка называется полюсом, если является бесконечной большой при
 ,
т.е.
,
т.е.

Точка называется существенно особой точкой, если не существует.( кроме случая(2)).
Определение 2. Вычетом функции в изолированной особой точке называется число
 ,
которое обозначается
,
которое обозначается
 ,
где
,
где
 достаточно малая окружность
достаточно малая окружность
 ,
причём величина вычета не зависит от
при достаточно малых
,
причём величина вычета не зависит от
при достаточно малых

Лекция 13
Тема: Операционное исчисление.
13.1 Преобразование Лапласа.
Определение 1. Функцией – оригиналом называется комплексная функция f(t) действительного аргумента t, удовлетворяющая следующим условиям:
f(t) непрерывна вместе со своими производными достаточно высокого порядка на всей оси t, кроме отдельных точек, в которых f(t) или её производные терпят разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек имеется лишь конечное число.
При t<0, f(t)=0
f(t) возрастает не быстрее показательной функции, т.е. существуют такие постоянные, M,
 ,
,
 ,
что для всех t
выполняется неравенство
,
что для всех t
выполняется неравенство
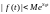
Число называется показателем роста f(t), для ограниченных функций =0.
Простейшей
функцией оригиналом является единичная
функция

Если
функция
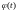 удовлетворяет условиям 1) и 3), но не
удовлетворяет условию 2), то произведение
удовлетворяет условиям 1) и 3), но не
удовлетворяет условию 2), то произведение
 удовлетворяет всем условиям 1), 2), 3).
Например, оригиналами будут функции
удовлетворяет всем условиям 1), 2), 3).
Например, оригиналами будут функции
 и т.д. Для простоты записи множитель
и т.д. Для простоты записи множитель
 будем
опускать, условившись, что все функции
f(t),
при t<0
равны 0. Например, вместо
будем
писать 1, вместо
будем
опускать, условившись, что все функции
f(t),
при t<0
равны 0. Например, вместо
будем
писать 1, вместо
 будем писать
будем писать
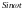 и т.д.
и т.д.
Определение
2:
Изображением функции f(t)
по Лапласу называют функцию комплексного
переменного
 ,
определенную отношением:
,
определенную отношением:

Фразу:
«функция f(t)
имеет своим изображением F(p)»
будем записывать символом
 или
или
 .
.
Пример
1:
 .
Действительно 1
.
Действительно 1
 .
.
Пример
2:

 Имеем:
Имеем:

Непосредственно из свойств интеграла получаем:
Свойство линейности.
 ,
где
,
где



Пример
3:

Теорема подобия.
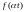 .
Доказательство.
=
.
Доказательство.
=
В
интеграле сделаем замену

=
 .
.
Дифференцирование оригинала.
Если
 или
вообще
или
вообще
 является оригиналом, то
или
является оригиналом, то
или
,
где под
 понимаем
правое предельное значение
понимаем
правое предельное значение
 .
.
Дифференцирование изображения.

Интегрирование оригинала.

Интегрирование изображения.
 ,
где путь интегрирования лежит в
полуплоскости
,
где путь интегрирования лежит в
полуплоскости
 .
.
Пример
4.
Найти изображение функции
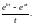
Из
примера 2 и свойства 1 имеем:
 Пользуясь
свойством 6, получаем
Пользуясь
свойством 6, получаем
 .
.
Пример
5.

Пример
6.

Таблица оригиналов и изображений
№ n/n |
Оригинал
|
Изображение
|
1 |
1 |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
sin(t- |
|
20 |
cos(t- ) |
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
Erf |
|
25 |
Si
t = |
|
26 |
Ci
t = - |
|
27 |
|
ln |
28 |
|
|
29 |
|
|
30 |
|
|


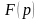

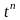 (n=1,
2, …)
(n=1,
2, …)
 (
(

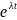 (
(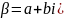





 (
(


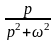



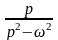








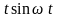






 )
(
)
(








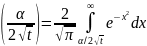




 ln
ln



 (
(