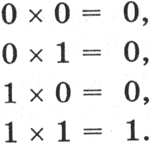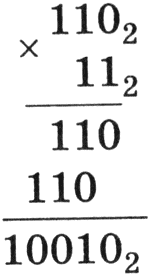Кодирование графических данных

Если рассмотреть с помощью увеличительного стекла черно-белое графическое изображение, напечатанное в газете или книге, то можно увидеть, что оно состоит из мельчайших точек, образующих характерный узор, называемый растром.

Поскольку линейные координаты и индивидуальные свойства каждой точки (яркость) можно выразить с помощью целых чисел, то можно сказать, что растровое кодирование позволяет использовать двоичный код для представления графических данных. Общепринятым на сегодняшний день считается представление черно-белых иллюстраций в виде комбинации точек с 256 градациями серого цвета, и, таким образом, для кодирования яркости любой точки обычно достаточно восьмиразрядного двоичного числа.

Для кодирования цветных графических изображений применяется принцип декомпозиции произвольного цвета на основные составляющие. В качестве таких составляющих используют три основных цвета: красный (Red, R), зеленый (Green, G) и синий (Blue, B). На практике считается (хотя теоретически это не совсем так), что любой цвет, видимый человеческим глазом, можно получить путем механического смешения этих трех основных цветов. Такая система кодирования называется системой RGB по первым буквам названий основных цветов.

Если для кодирования яркости каждой из основных составляющих использовать по 256 значений (восемь двоичных разрядов), как это принято для полутоновых черно-белых изображений, то на кодирование цвета одной точки надо затратить 24 разряда. При этом система кодирования обеспечивает однозначное определение 16,5 млн различных цветов, что на самом деле близко к ­чувствительности человеческого глаза. Режим представления цветной графики с использованием 24 двоичных разрядов называется полноцветным (True Color).

Если уменьшить количество двоичных разрядов, используемых для кодирования цвета каждой точки, то можно сократить объем данных, но при этом диапазон кодируемых цветов заметно сокращается. Кодирование цветной графики 16-разрядными двоичными числами называется режимом High Color.

Системы счисления

Позиционные и непозиционные системы счисления.

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Рассмотрим арабскую и римскую систему счисления. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:

11 – здесь первая единица обозначает десять, а вторая – 1. II – здесь обе единицы обозначают единицу.

345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.

XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Перевод чисел в позиционных системах счисления (СС). Перевод чисел из любой позиционной СС в десятичную

Мы пользуемся свернутой формой записи числа, но мы знаем, что, например, число 352 = 3*100+5*10+2.

В развернутой форме производится умножение цифр числа на степень основания, т.е. 352=3*102+5*101+2*100.

Т.о. любое число в позиционной СС можно записать в развернутой форме и перевести в десятичную СС.

В памяти компьютера числа представлены в двоичной СС, поэтому в информатике часто возникает необходимость перевода чисел из двоичной системы в десятичную и обратно. Приведем пример перевода двоичного числа:

Пример 1:

5 4 3 2 1 0 1101012 = 1*25 + 1*24 + 0*23 + 1*22 + 0*21 + 1*20 = 32 + 16 + 0 + 4 + 0 + 1 = 5310.

Пример 2: Двоичное число с дробной частью

3210-1-2 1001,112 = 1*23 + 0*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2 = 8 + 1 + 1/2 + 1/4 = 9+ 0,75 = 9,7510.

По такому же принципу можно переводить числа в десятичную СС из других позиционных СС.

Пример 3:

32114 =  3*43 + 2*42 + 1*41 + 1*10 = 3*64 + 2*16 + 1*4 + 1*1 = 192 + 32 + 4 + 1 = 22910

Пример 4:

2148 = 4 * 80 + 1 * 81 + 2 * 82 = 4 + 8 + 128 = 14010

Пример 5:

2 1 0 2AF16 =  2*162 + 10*161 + 15*160 = 2*256 + 10*16 + 15*1 = 512 + 160 + 15 = 68710

В записи числа в шестнадцатеричной системе счисления А=10 и F=15.

Перевод чисел из десятичной СС в любую позиционную систему счисления.

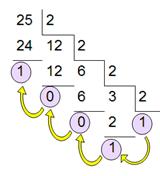
Существует алгоритм перевода целого десятичного числа в двоичное:

Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание СС (на 2)  до тех пор, пока частное от деления  не окажется меньше основания СС (<2). Записать полученные остатки в обратной последовательности, начиная с последнего результата.

2510 = 110012

Для перевода дробных десятичных чисел существует тоже алгоритм. Для этого необходимо  отдельно перевести целую и дробную часть.

26, 7510 = 26 + 0,75 = 11010+0,11 = 11010,112

Целую часть переведем как указано выше, а дробную часть переведем по следующему алгоритму:

последовательно умножать исходную и получаемые дробные части на основание системы до тех пор, пока не получим нулевую дробную часть. Записать полученные целые части произведений в прямой последовательности.

0, 75   *2 1 1, 5   *2 1 1, 0   Поучаем 0,7510 = 0,112

Используя данный алгоритм можно перевести десятичное число в позиционную систему с любым основанием.

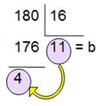
18010 = B416

3. Арифметические операции в позиционных системах счисления.

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам.

Сложение. Рассмотрим сложение чисел в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:

0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10

Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания.

Сложение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа 110₂ и 11₂:

Проверим правильность вычислений сложением в десятичной системе счисления. Переведем двоичные числа в десятичную систему счисления и затем их сложим:

110₂ = 1 × 2² + 1 × 2¹ + 0 × 2⁰ = 6₁₀;

11₂ = 1 × 2¹ + 1 × 2⁰ = 3₁₀;

6₁₀ + 3₁₀ = 9₁₀ .

Теперь переведем результат двоичного сложения в десятичное число:

1001₂ = 1 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰ = 9₁₀ .

Сравним результаты - сложение выполнено правильно.

Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой:

Вычитание многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей вычитания с учетом возможных заемов из старших разрядов. В качестве примера произведем вычитание двоичных чисел 110₂ и 11₂:

Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел:

Умножение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на цифры множителя. В качестве примера произведем умножение двоичных чисел 110₂ и 11₂:

Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 110₂ на 11₂:

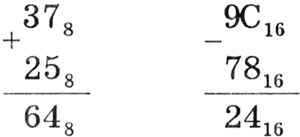
Арифметические операции в восьмеричной и шестнадцатеричной системах счисления. Аналогично можно выполнять арифметические действия в восьмеричной и шестнадцатеричной системах счисления. Необходимо только помнить, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления:

Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему.