Интегрирование заменой переменной (подстановкой)

Замена переменной – один из самых эффективных приемов интегрирования, который основывается на следующем.

Пусть требуется найти В ряде случаев удается выбрать в качестве новой переменной такую дифференцируемую функцию , что имеет место равенство , причем функция легко интегрируется, т.е.

Тогда

Удачная замена переменной позволяет упростить исходный интеграл и в ряде случаев свести его к табличному интегралу.

Пример 5.2. Найти

Решение. Положим . Тогда . Умножим и разделим исходный интеграл на число 3 и выполним следующие преобразования

Полученный интеграл относится к табличным и, следовательно,

Сделаем проверку дифференцированием :

.

Полученная производная совпадает с подынтегральной функцией исходного

интеграла, что говорит о правильности вычислений.

Пример 5.3. Вычислить

Решение. Чтобы выявить замену, посредством которой может быть вычислен этот интеграл, преобразуем его к виду

Если положить , тогда и в результате получим

Интегрирование по частям

Пусть функции дифференцируемы и существует первообразная для функции Тогда существует первообразная и для функции причем справедлива формула

,

называемая формулой интегрирования по частям.

Пример 5.4. Найти

Решение. Положим Тогда

Произвольную постоянную в этих случаях исключают и записывают

Теперь, применяя формулу интегрирования по частям, получим

Иногда формулу интегрирования по частям приходится применять неоднократно.

Пример 5.5. Вычислить

Решение. Полагая , имеем , .

Применяя формулу интегрирования по частям, получим:

Степень переменной в подынтегральном выражении уменьшилась на единицу. Повторим приём интегрирования по частям. Положим

Отсюда

Тогда +

Вопросы для самоконтроля

1. Дайте определение первообразной функции.

2. Что называют неопределенным интегралом?

3. Перечислите основные свойства неопределенного интеграла.

4. В чем суть приема, называемого заменой переменной?

5. На чем основан метод интегрирования по частям?

Задачи для самостоятельной работы

Найти неопределенные интегралы, результаты проверить дифференцированием:

Таблица 5.2

Номер варианта	А)	Б)
1
2
3
4
5
6
7
8
9
10

6. Определенный интеграл

Пусть функция определена на отрезке . Разобьем отрезок на элементарных отрезков точками . В каждом из отрезков разбиения выберем произвольную точку и положим , где . Тогда сумма вида

называется интегральной суммой для функции на отрезке .

Пусть существует и конечен предел интегральной суммы при стремлении к нулю длины максимального элементарного отрезка независимо от способа разбиения отрезка на части и выбора на них точек . Тогда функция называется интегрируемой на , а число - определенным интегралом от на и обозначается

.

Основные свойства определенного интеграла:

1. Постоянная величина может быть вынесена за знак интеграла

.

2. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций

.

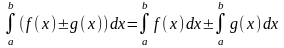3. При перестановке пределов интеграл меняет знак на обратный

.

4. Интеграл с равными пределами равен нулю

.

5. Если функция интегрируема в наибольшем из отрезков , то справедливо равенство:

.

6. Теорема о среднем для непрерывной функции на отрезке

, где .

7. Формула Ньютона-Лейбница (основная формула интегрального исчисления)

,

где - некоторая первообразная функции на отрезке .

Определенный интеграл используют для вычисления площадей плоских фигур. Пусть на плоскости задана фигура, определяемая кривыми

Рис. 6.1

и прямыми линиями (рис.6.1).

Если на отрезке , то площадь фигуры, заключенная между кривыми и на этом отрезке определяется формулой

.

Понятие определенного интеграла используется также в экономике. Пусть функция описывает изменение производительности некоторого производства во времени. Тогда объем продукции , произведенной за промежуток времени , вычисляется с помощью определенного интеграла:

.

Пример 6.1. Вычислить определенный интеграл .

Решение. Подынтегральная функция является степенной и для неё известна первообразная . Отсюда по формуле Ньютона-Лейбница

= .

Пример 6.2. Вычислить определенный интеграл .

Решение. Сделаем замену переменной . Найдем пределы интегрирования для переменной : если , то , если , то . Далее , , , . Искомый интеграл преобразуется к виду:

= = .

Пример 6.3. Найти площадь фигуры, ограниченной линиями: , .

Решение. Искомая фигура представлена на рис.6.2:

Найдем пределы интегрирования путем решения системы уравнений:

Приравнивая правые части уравнений, получим . Отсюда имеем . Тогда искомая площадь вычисляется по формуле

.

Пример 6.4. Изменение производительности производства с течением времени от начала внедрения нового технологического процесса задается функцией , где - время в месяцах. Найти объем продукции, произведенной за третий месяц.

Решение. Объем продукции находим по формуле