5. Қисық сызықты қозғалыстағы жылдамдық жəне үдеу.
Егер материалдық нүкте қозғалғанда оның траекториясы қисық сызық болып келсе, онда қозғалыс қисық сызықты қозғалыс деп аталады. Енді осы қисық сызықты қозғалыс кезіндегі жылдамдықпен үдеудің өзгерісін қарастырайық.
Қисық сызықты қозғалыс кезінде жылдамдық векторы берілген әрбір уақыт мезетінде дене траекториясына қозғалыстың бағыты бойынша жүргізілген жанама бойымен бағытталады. Дененің MN қисық сызығының бойымен қозғалысын қарастырайық.(4-сурет).
Айталық
M және N нүктелеріндегі қозғалыс
жылдамдықтары
және
болсын. Ал M нүктесіндегі үдеу (1.2.9)
өрнекке сәйкес мына шамаға тең.
4
– суретте көрсетілгендей
бойына
-ға
тең
және
кесінділерін аламыз. Сонда үдеуді
былайша өрнектейміз:
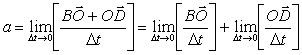
өрнектің
екінші құраушысы
жанама немесе тангенциал үдеу деп
аталады, себебі Δt→0
кезде
OD кесіндісі M нүктесінің маңында айналып,
траекторияның жанамасымен беттесуге
ұмтылады. Оның сан мәні мынаған тең:
(1.3.3)
Сонымен
үдеу қозғалыс жылдамдығының сан жағынан
өзгерісін көрсетеді. Кез келген бірқалыпты
қозғалыс үшін
болады. Ал (1.3.2)- өрнектің бірінші құраушысы
нормаль немесе центрге тартқыш үдеу
деп аталады, себебі Δt→0
кезде
Δt→0
да, M нүктесіндегі
жанамаға перпендикуляр болады. Сөйтіп,
нормаль үдеудің сан мәні мына шамаға
тең:
Енді
ВО кесіндісінің мәні неге тең болатынын
қарастырайық. ΔМВО-дан
Δα
бұрышын шексіз аз шама деп есептесек,
ВО=MB
Δα=vΔα,
өйткені
.
Сонымен нормаль үдеуді мына түрде жазуға
болады:
Бұл
өрнектің оң жағын Δs–ке
көбейтіп және бөлейік, сонда ол
түрге келеді. Мұндағы Δs
– MN доғасының
ұзындығы. Егер геометрия курсынан қисық
сызықтың қисықтығы деген ұғымды еске
алатын болсақ, онда 4-суретке сәйкес
Δs=RΔα
. мұндағы R-қисықтық
радиусы,Δα
- центрлік бұрыш. Олай болса,Δα/
Δs=1/R
және M
нүктесіндегі
жылдамдық Δt
уақыт өзгерісіне тәуелді болмайды.
Сөйтіп
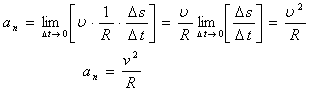(1.3.4)
Сонымен,
қисық сызықты қозғалыс кезінде нормаль
үдеу қозғалыс жылдамдығы бағытының
өзгерісін көрсетеді. Кез келген түзу
сызықты қозғалыс үшін
.
теңдіктен материалдық нүктенің қисық
сызықты қозғалысы кезіндегі толық
үдеуі
оның нормаль және тангенциал үдеулері
векторларының қосындысына тең екендігін
көреміз:
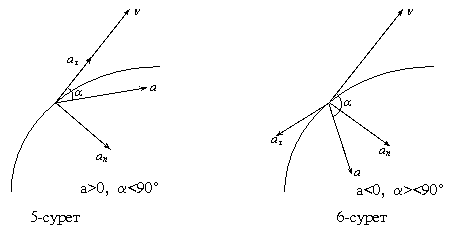
Толық үдеудің бағытын тангенциал үдеу
мен толық үдеу немесе нормаль үдеу мен
толық үдеу арасындағы бұрыш арқылы
көрсетуге болады :
(1.3.6)
6. Айналмалы қозғалыс. Бұрыштық жылдамдық жəне бұрыштық үдеу.
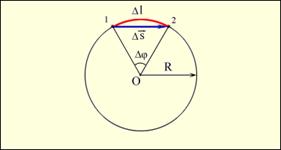
Шеңбер
бойымен қозғалыс. Дененің
шеңбер бойымен қозғалысы қисық сызықты
қозғалыстың
дербес
жағдайы болып табылады.
орын ауыстыру векторымен қатар радианм
ен
өлшенетін
бұрыштық
орын ауыстыруын қарастыру ыңғайлы.
Доғаның ұзындығы бұрылу бұрышымен
Δl = RΔφ.
қатынаспен байланысты. Бұрылу бұрышы
аз болған кезде Δl ≈ Δs.
.-сурет. Дененің шеңбер бойымен сызықты және бұрыштық орын ауыстыруы.
Шеңбер
траекториясының берілген нүктесіндегі
бұрыштық жылдамдық
деп кішкентай бұрыштық орын ауыстыруының
кішкентай
уақыт аралығына қатынасының шегін
айтады.
Бұрыштық
жылдамдық рад/с өлшенеді. Сызықтық
жылдамдығы мен бұрыштық
жылдамдығының арасындағы байланыс
υ = ωR.
Дененің шеңбер бойымен бірқалыпты
қозғалыс кезінде υ
және ω
шамалары тұрақты болады. Бұл жағдайда
векторының бағыты ғана өзгереді.
Дененің шеңбер бойымен бірқалыпты қозғалысы үдемелі қозғалыс болып табылады.
Айналыс
бір қалыпты болмаған жағдайда бұрыштық
жылдамдық ω
уақытқа байланысты өзгереді. Осындай
өзгерісті сипаттау үшін бұрыштық үдеу
(β)деген ұғым енгізіледі. Бірқалыпты
айнымалы айналма қозғалыстың бұрыштық
үдеуі дегеніміз бұрыштық жылдамдықтың
өзгерісіне тура пропорционал және осы
өзгеріс болуына кеткен
уақыт аралығына кері пропорционал болып
келген физикалық шама (β) болады. Бұрыштық
үдеу —
бұрыштық жылдамдықтың өзгеру
шапшаңдығын сипаттайтын векторлық шама;
- бұрыштық жылдамдық өзгерісінің осы
өзгеріс өткен уақыт аралығына қатынасымен
анықталатын бұрыштық жылдамдықтың
өзгеруінің лездігі. Бұрыштық үдеудің
бірліктердің халықаралық
жүйесіндегі бірлігі:
рад/с2. Айналыс
бір қалыпты болмаған жалпы жағдайда,
берілген уақыт кезеңіндегі бұрыштық
үдеу мынаған тең: 
Дифференциалдық
есептеуден: 
сонда бұрыштық үдеу: 
