
- •1.Механикалық қозғалыс. Механикалық жүйе. Механиканың негізгі моделі: материалдық нүкте, қатты дене, тұтас орта.
- •2.Механиканың негізгі ұғымдары: радиус-вектор, траектория, орын ауыстыру, жол.
- •3.Механиканың негізгі ұғымдары: жылдамдық, орташа жəне лездік жылдамдық.
- •4. Үдеу. Үдеудің нормал жəне тангенциал құраушылары. Толық үдеу.
- •5. Қисық сызықты қозғалыстағы жылдамдық жəне үдеу.
- •6. Айналмалы қозғалыс. Бұрыштық жылдамдық жəне бұрыштық үдеу.
- •7. Механикадағы күштер: ауырлық күші жəне дененің салмағы.
- •11.Ньютонның заңдары.
- •17.Кейбір денелердің инерция моменттері: цилиндр және диск.
- •18.Механикалық жұмыс.Қуат
- •21.Сұйықтың қозғалысы. Стационар ағыс. Сығылмайтын сұйықтық
- •25.Сұйықтың тұтқырлығы.
- •26.Механикалық тербелістер. Математикалық маятник.
- •29. Толқындар. Толқынның түрлері. Толқындардың негізгі сипаттамалары. Допплер эффектісі
- •31.Термодинамикалық жүйе. Термодинамикалық параметрлер. Термодинамикалық процесс. Қайтымды және қайтымсыз процестер.
- •34. Идеал газ. Идеал газ күйінің теңдеуі.
- •35,36,38. Iшкi энергия. Жылу мөлшері және термодинамикалық жұмыс.
- •56.Электр қозғаушы күші.
- •74.Диэлектриктер. Диэлектриктердi поляризациялау
- •72.73.Электр өрiсiнiң .Энергиясы. Конденсаторды тiзбектей және параллель жалғау
- •. 77 Импульстің сақталу заңы
- •78Энергияның сақталу заңы
- •81.Лоренц түрлендірулері
- •88Энтропия және ықтималдылық
- •Техникалық вакуум[өңдеу]
- •Физикалық вакуум
88Энтропия және ықтималдылық
-

Бұл мақаланы Уикипедия сапа талаптарына cәйкес болу үшін жетілдіру қажет. Осы мақаланы әрі қарайдамытуға көмек беріңіз.
Энтропия (грек. еntropіa – бұрылыс, айналу) – тұйық термодинамикалық жүйедегі өздігінен жүретін процестің өту бағытын сипаттайтын күй функциясы. Энтропияның күй функциясы екендігі термодинамиканың екінші бастамасында тұжырымдалады. Энтропия ұғымын термодинамикаға 1865 ж. Р.Клаузиус енгізген. Кез келген А және В күйлеріндегі жүйе Энтропиясы мәндерінің айырымы мына формула арқылы анықталады: , мұндағы Q – жүйеге күйі шексіз аз квазистатик. болып өзгергенде берілетін жылу мөлшері, Т – жүйенің абс. темп-расы; интрегал екі күйді өзара жалғастыратын кез келген қайтымды жолмен алынады. Изотерм. процесс жағдайында: S=Q/Т. Ал кез келген қайтымды жолмен алынатын тұйық процесс үшін: . Соңғы теңдік Энтропияның dS=Q/Т түріндегі толық дифференциал болатындығының қажетті және жеткілікті шарты, ал Энтропия – күй функциясы. Энтропияның абс. мәні термодинамиканың үшінші бастамасы бойынша анықталады және ол бойынша абс. нөл темп-рада кез келген жүйенің Энтропиясы нөлге айналады. Адиабаталық оңашаланған жүйелеріндегі қайтымды процестер кезінде Энтропияның мәні тұрақты болып қалады да, қайтымсыз процестер кезінде Энтропияның мәні артады; барлық реал процестерінде Энтропияның мәні артады (Энтропияның арту заңы). Статист. физикада Энтропия статист. салмақ () деп аталатын шамамен байланыстырады. Больцман принципіне сәйкес: S=kІn, мұндағы k – Больцман тұрақтысы. Сонымен Энтропия – термодинам. тепе-тендік күйдегі макроскоп. денелерге тән қасиет. Ол бірліктердің халықаралық жүйесінде (СИ) Дж/К арқылы өрнектеледі. Энтропия ұғымы ғылымның көптеген салаларында (физика, химия, т.б.) маңызды рөл атқарады. С. Асанов[1]
Еркінше алынған қайтымды циклды қарастыралық. Циклды бөлшектеу көмегімен, элементарлы Карно циклын шексіз көп санды теңдікті, мына түрде жазуға болады:
dq1T1= dq2T2
Тұйықталған пішін бойынша, интегралдау кезінде және dq2 теріс таңбаларын есептеп табамыз.
ʃdqқайтT1 = 0.
Мұндағы, dqқайт - таңбасы кезіндегісі, қаралып отырған айналмалы процесстегі қайтымды түріне, ерекше көңіл аударылуы тиіс. Сонымен, келтірілген жылулықтың интегралды суммасы үшін, қандай болса да, қайтымды циклда нөлге тең. Бұл Клаузиус теңдеуі деп аталады. Жылу динамикасында формуласын Клаузиус теңдеуі деп, ал формуласының оң жақ бөлігінің теңдеуін, Клаузиус интегралы деп атайды. Қандай да тұйық жол үшін, математикалық қажетті және жеткілікті шарт, ол:
ds = dq/T
толық дифференциал болады. 1-2 еркінше алынған жол бойындағы интеграл, әр уақытта тең:
Шарт бойынша, жылулықты dq жеткізу процессі қайтымды деп есептеледі. Сонымен, S - функция жағдайы. Оны энтропия деп атайды. Формуладағы 1/T үстіңгі көрсеткішінде тұрған, толық емес дифференциал dq үшін интегралдаушы көбейткіш болады. Еркін қайтымды айналмалы процесс үшін алынған формуладан, энтропия S және абсолютты температура Т бар екендігі туралы тікелей қорытынды шығады да, теңдеумен анықталады, оны қайтымды процесстер үшін, жылу динамикасының екінші заңының теңдеуі деп атайды.
Қайтымды изотермиялық процесс (T=const) кезіндегісін теңдеуден табамыз:
Қайтымды адиабатты процесс кезіндегі, dq=0 болғанда:
ds = 0; S2 - S1 = 0; S = const.
Қайтымды адиабатты процесс, энтропияның өзгеруін болдырмайды. Сондықтан, оны, изоэнтропийлі процесс деп атайды. Екі рет кездесетін көрсеткіштердің бар болуына сәйкес, сыртқы ортамен, энергетикалық пішіндегі әрекетте болуы. Әрекеттік шарты үшін, байланыстырушы температура Т жылу алмасуы және меншікті энтропия S жолымен, осындай қос көрсеткіштерді құрады. Энтропия экстенсивті (аудитивті) шама болады, себебі энтропия зат, осыған қарағанда оның анықтамасы, осы заттардың (S = mS) санды мөлшеріне пропорционалды, Т мұнда S функциясында болады.
Энтропияның абсолютты шамасын, кейбір тұрақты дәлдікпен есептеуге болады. Себебі, оның абсолютты шамасына емес, энтропиялық өзгеруіне жиі көңіл аударады, оның бастапқы есептелуін шартты түрде таңдайды (әрекеттегі қалыпты физикалық күй, ал су үшін, үш қатты нүкте күйі). Энтропия бірлігі - Дж/(кгК). Химиялық реакцияны зерттеу кезінде тұрақтыны білу үшін, энтропияның абсолютты шамасының бастапқысын есептеуі үшін өте үлкен практикалық мәні бар. Нернстің ашқан принципінің атауындағы, Нернстің жылулық теоремасымен көрсетілген тұрақтылығын таңдауды іске асыруға болады. Теореманың тұжырымдауына байланысты, қандай да болмасын жүйенің энтропиясы кезіндегі абсолютты нольде, әр уақытта нөлге тең жағдайында қабылдануы мүмкін.
limsr->0 = 0
Бұдан көрінгендей, жүйелер жағдайының T—> К температура кезіндегі, барлық мүмкіндік өзгеруі, энтропияның тұрақты кезінде өтеді. Сондықтан, жүйелер күйінің (қалай болса солай) Т= 0 К кезіндегісін бастапқы есептеу үшін таңдайды. Сонымен, қайтымды процесстер бойынша алынған интеграл
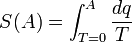 ,
,
T=K кезіндегі, қалай болса солай алынған бастапқы жағдайының, А жағдайына арналған энтропияның абсолютты шамасын көрсетеді.
Нернст принципі, тәжірибе жолымен анықталған. Ол, статистикалық механиканың теориялық дәледенуімен табылады. Бұл жерде, мыналарды атап өту керек. Өйткені Нернстің теоремасына байланысты, энтропия - абсолютты нөл айналасында, қандай да өзгеру күйі кезінде, өзгеріске ұшырамайды, сондықтан заттар, жылу алмасуға қабілетсіз болады, онда, бұдан шығуы, салдар ретінде есептелген, осы Нернстің тұжырымдауынша, жылу динамикасының үшінші заңы бойынша, жылуды алып кету жолымен, абсолютты нөлге қол жетпестігі туралы айтылады. Атап айтқанда, Т2 = 0 К температуралы суықтық көзінен, Карно циклын жүргізуге болмайды және осыған сәйкес пайдалы эсер коэффициенті ηк = 1
Ықтималдылық
Теориясы –
кездейсоқ бір оқиғаның ықтималдығы
бойынша онымен қандай да бір байланыста
болатын басқа бір кездейсоқ оқиғаның
ықтималдығын анықтауға мүмкіндік
беретін математика білімі. Ықтималдылық
теориясында кездейсоқ құбылыстардың
заңдылығы зерттеледі. Кездейсоқ
құбылыстарға анықталмағандық, күрделілік,
көп себептілік қасиеттері тән. Сондықтан
мұндай құбылыстарды зерттеу үшін арнайы
әдістер құрылады. Ол әдістер мен тәсілдер
Ықтималдылық теориясында жасалынады.
Мысалы, біркелкі болып келетін кездейсоқ
құбылыстарды жан-жақты бақылай отырып
қандай да болмасын бір заңдылықты
(тұрақтылықты), яғни статистик. заңдылықты
байқаймыз. Ықтималдылық теориясының
негізгі ұғымдары элементар ықтималдылық
теориясы шегінде қарапайым түрде
анықталады. Элементар ықтималдылық
теориясында қарастырылатын әрбір сынау
(Т) Е1,Е2, ...,Еs оқиғаларының тек қана
біреуімен ғана аяқталады. Бұл оқиғалар
сынау нәтижесі (қорытындысы) деп аталады.
Әрбір Еk нәтижесімен оның ықтималдығы
деп аталатын рk оң саны байланыстырылады.
Бұл жағдайда рk сандарының қосындысы
бірге тең болуы керек. А оқиғасы тең
мүмкіндікті бірнеше оқиғаларға (Еі ,Еj
, …, Еk) бөлінеді және олардың кез келген
біреуінің (не Еі , не Еj ,…, не Еk) пайда
болуынан А оқиғасының пайда болуы
шығады. Сынау нәтижесінде А оқиғасы
бөлінетін мүмкін мәндері (Еі E,j , …, Еk)
осы оқиғаға (А-ға) қолайлы жағдайлар деп
атайды. Анықтама бойынша А оқиғасының
р(А) ықтималдығы оған қолайлы жағдайлар
нәтижелері ықтималдықтарының қосындысына
тең деп ұйғарылады: P(A)=Pі+Pj+...+Pk (1) Дербес
жағдайда р1=р2=...=рs=1/s болғанда Р(А) =r/s (2)
болады. А оқиғасына қолайлы жағдайлар
нәтижесі санының (r) барлық тең мүмкіндікті
нәтижелер санына (s) қатынасы А оқиғасының
ықтималдығы деп аталады. (2) формула
ықтималдықтың классикалық анықтамасын
өрнектейді. Бұл анықтама “ықтималдық”
ұғымын дәл анықтамасы берілмейтін “тең
мүмкіндік” (тең ықтималдық) ұғымына
келтіреді. Тең мүмкіндік немесе тең
ықтималдық ұғымдары алғашқы ұғымдарға
жатады.Олар логикалық (формалды) анықтама
беруді қажет етпейді. Егер жалпы сынау
нәтижесінде бірнеше оқиғалар пайда
болса және олардың біреуінің пайда болу
мүмкіндігінің екіншісіне қарағанда
артықшылығы бар деп айта алмасақ (яғни
сынаулар нәтижесінде симметриялы
қасиеті болса) онда мұндай оқиғалар тең
мүмкіндікті делінеді. Элементар
ықтималдылық теориясының негізгі
формулаларының қатарына ықтималдылықтардың
толық формуласы да жатады: егер А1,
А2,..., Аr оқиғалары қос-қостан үйлесімсіз
болып әрі олардың бірігуі нақты бір
оқиға болса, онда кез келген В оқиғасының
ықтималдылығы: Р(В)=![]() Р(В/Аk)Р(Аk)
қосындысына тең болады. Ықтималдылық
теориясының негізін құрудағы қазіргі
ең жиі тараған логик. сұлбаны 1933 ж. кеңес
математигі А.Н. Колмогоров жасаған. Бұл
сұлбаның негізгі белгілері төмендегідей.
Ықтималдылық теориясының тәсілдерімен
қандай да болмасын нақты бір есепті
зерттегенде ең алдымен U элементтерінің
(элементар оқиғалар деп аталатын) U жиыны
бөлініп алынады. Кез келген оқиға оған
қолайлы жағдайлардың элементар
оқиғаларының жиыны арқылы толық
сипатталынады. Сондықтан ол элементар
оқиғалардың белгілі бір жиыны ретінде
де қарастырылады. Белгілі бір А оқиғалары
мен олардың ықтималдығы деп аталатын
Р(А) сандары байланыстырылады және олар
мынадай шарттарды қанағаттандырады:
Р(В/Аk)Р(Аk)
қосындысына тең болады. Ықтималдылық
теориясының негізін құрудағы қазіргі
ең жиі тараған логик. сұлбаны 1933 ж. кеңес
математигі А.Н. Колмогоров жасаған. Бұл
сұлбаның негізгі белгілері төмендегідей.
Ықтималдылық теориясының тәсілдерімен
қандай да болмасын нақты бір есепті
зерттегенде ең алдымен U элементтерінің
(элементар оқиғалар деп аталатын) U жиыны
бөлініп алынады. Кез келген оқиға оған
қолайлы жағдайлардың элементар
оқиғаларының жиыны арқылы толық
сипатталынады. Сондықтан ол элементар
оқиғалардың белгілі бір жиыны ретінде
де қарастырылады. Белгілі бір А оқиғалары
мен олардың ықтималдығы деп аталатын
Р(А) сандары байланыстырылады және олар
мынадай шарттарды қанағаттандырады:
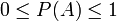 ,
,Р(U)=1,
Егер А1, ..., Аn
оқиғалары қос-қостан үйлесімсіз болып, ал А – олардың қосындысы болса, онда: Р(А)=Р(А1)+Р(А2)+...+Р(Аn) болады. Толық матем. теория құру үшін 3-шарттың қос-қостан үйлесімсіз оқиғалардың шектеусіз тізбегі үшін де орындалуы қажет. Теріс еместік пен аддитивтілік қасиеттері – жиын өлшеуінің негізгі қасиеттері. Сондықтан Ы. т. формалды түрде өлшеуіштер теориясының бөлігі ретінде де қарастырылуы мүмкін. Бұл тұрғыдан қарағанда Ы. т-ның негізгі ұғымдары жаңа мәнге ие болады. Кездейсоқ шамалар өлшемді функцияларға, ал олардың матем. үміті А.Лебегтің абстракт интегралына айналады, тағы басқа. Бірақ ықтималдылық теориясы мен өлшеуіштер теориясының негізгі мәселелері әр түрлі болып келеді. Ықтималдылық теориясының негізгі, өзіне тән ұғымына оқиғалардың, сынаулардың, кездейсоқ шамалардың тәуелсіздік ұғымы жатады. Сонымен бірге ықтималдылық теориясында шартты үлестіру, шартты матем. үміт, тағы басқа объектілер де зерттеледі. Ықтималдылық теориясы 17 ғ-дың орта кезінде пайда болды.
89молекулалардың соқтығысуы молекулалардың эффкутифті диаметрі
