7. Аналитикалық геометрияның қарапайым есептері (екі нүктенің арақашықтығы; берілген кесіндіні белгілі қатынаста бөлу). Екі нуктенін ара қашықтығы

Жазықтықта және екі нүкте берілсін. Осы екі нүкте арақашықтығын, немесе АВ кесіндісінің ұзындығын, мына формуламен есептейді:

.

Кесіндіні берілген қатынаста бөлу

Жазықтықта және екі нүкте берілсін. АВ кесіндісін АМ:МВ= болатындай қатынаспен бөлетін М(х,у) нүктесінің координаталары мынадай формуламен есептелінеді:

, . Дербес жағдайда, АВ кесіндісін тең екіге бөлу керек болса, яғни + =1:1=1, формула былай түрленеді: ,

. Нүктеден жазықтыққа дейінгі қашықтық. нүктесінен жазықтығына дейінгі қашықтық формуласы бойынша табылады. Нүкте мен координаталар басы берілген жазықтың екі жағында жатса, онда , егер нүкте мен О нүктелері берілген жазқытықтың бір жағында жатса, болады. Егер қашықтықтың өзі ғана керек болса, онда формуласы қолданылады

8. Векторлар және оларға қолданылатын сызықтық амалдар. Екі вектордың скалярлық көбейтіндісі. Вектор және оған амалдар қолдану

Негізгі ұғымдар. Мектеп курсынан белгілі векторлар жөніндегі білімімізді жалпылайық.

Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды немесе , кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді ( = , , а). векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және деп белгілейді. Басы мен соңы беттесетін вектор нолдік вектор деп аталады, = және ұзындығы нолге тең.Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады. және векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:

және векторларының - айырымы деп -ға қосқанда

векторы алынатын = - векторын айтады.

векторының санға көбейтіндісі деп ұзындығы болатын, бағыты >0 болғанда векторымен бағыттас, <0 болғанда векторымен қарама-қарсы бағытта болатын векторын айтады. Суретте, = 2, =2 ; = -1, =- .

2Вектордың скаляр көбейтіндісі

Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусына көбейтіндісіне тең шаманы айтады: .

Тік бұрышты декарт координаталар жүйесінде векторының басы мен соңының координаталары белгілі болсын және . Сонда векторын координаталары арқылы былай жазуға болады: = векторының басы координаталар басымен беттесетіндей етіп өз-өзіне параллель көшірсек, онда векторының координатасы вектордың соңының координаталарымен бірдей болатынын аңғару қиын емес. Жазықтықта вектордың координатасын екі сан анықтаса, айталық , кеңістікте үш сан анытайды, .

Вектордың ұзындығы оның координаталарының квадраттарының қосындысынан алынған квадрат түбірге тең: . және векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады: .Ал векторын санға көбейту мынадай түрде анықталады: . және векторларының скаляр көбейтіндісі мынадай:

9. Жазықтықтағы түзудің теңдеулері. Жазықтықтағы түзу (1-сурет) Оу осін В(0;b) нүктесінде қиып, Ох осімен (0< < ) бұрыш жасасын. Түзу бойынан қандай да бір М(х,у) нүкте алайық. Түзудің Ох осімен жасаған бұрышының тангенсін ВМК үшбұрышынан табамыз:

; деп белгілеп, түзудің бұрыштық коэффициенті деп атау қабылданған. Сонымен: .

Осы қатынастан у-ті тапсақ: y=kx+b (2)

Түзу бойында жатқан кез келген нүктенің координатасы (2) теңдеуді қанағаттандырады да түзуден тыс жатқан нүктелер бұл теңдеуді қанағаттандырмайды. (2) теңдеу түзудің бұрыштық коэффициентімен берілген теңдеуі деп аталады. Дербес жағдайларын қарастырайық.

1. Түзудің бұрыштық коэффициентімен берілген теңдеуіндегі b=0 болсын. Онда түзу теңдеуі y=kx түрге келеді де, түзу координат басынан өтеді (2-сурет)

2. Егер болса, онда болады да, түзу теңдеуі y=b түрге келеді де, түзу Ох осіне параллель болады (3-сурет). Ал Ох осінің теңдеуі y=0 болады.

3. Егер болса, онда мәні болмайды, түзу Ох осіне перпендикуляр болады. Айталық түзу Ох осінен а тең кесінді қиып өтеді, сонда түзу теңдеуі х=а түрде болады (4-сурет). Ал Оу осінің теңдеуі х=0 болады.

Теорема. Тік бұрышты координаталар жүйесінде кез келген түзу бірінші ретті теңдеумен беріледі Ах+Ву+С=0 (3)

Және керісінше, (3) теңдеу (А, В, С коэффициенттердің бәрі бір мезгілде нолге тең болмаған кезде) тік бұрышты координаталар жүйесінде қандай да бір түзуді анықтайды.

(3) теңдеуді әдетте түзудің жалпы теңдеуі деп атайды

.Түзулердің параллельдік және перпендикулярлық шарттары

Егер екі түзу параллель болса, онда =0 болады да tg =0. Бұл жағдайда (7) формула мынадай түрге келеді: k₂ – k₁ = 0. Осыдан екі түзудің параллелдік шарты шығады: k₂ = k₁ , (8) яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше. Егер екі түзу перпендикуляр болса, онда болады да, , . Осыдан екі түзудің перпендикулярлық шарты шығады: k₂ = ,

яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше

10. Екінші peтті қисықтар жене олардың канондық теңдеулері

Жоғары математкада екінші дәрежелі теңдеулермен анықталатын сызықтарды екші pеттi қисықтар деп атайды. Олар негізінен , эллипс, гипербола және парабола деп аталады. Бұл қисықтар техника мен ғылым саласында иі кездеседі.

1. Эллипс. Фокустар деп аталатын берілген екі нүктеден қашықтықтарыньң қосындысы әрқашанда тұрақты шама болатын жазықтықтағы нұктелердің геометриялык орындарын эллипс деп атайды (9-сызба). Анықтама бойынша F₁M + F₂M = 2a

нүктелер,

М{х, у) -эллипстің бойындағы кез келген жылжымалы нүкте,

2а-тұрақты шама

Егер F₁F₂ = 2с десек, онда F₁(-C;0), F₂(C;0). Сонда:

Енді осы мәндерді қойсақ:

Немесе

Егер а>с болса, онда а² —с²=b² болады. Сондықтан эллипстің канондық теңдеуі деп аталатын теңдеуге келеміз:

Мұндағы х пен у эллипстің кез келген жылжымалы нүктесінің координаттары, а -эллипстің үлкен жарты oci, b -онын кіші жарты oci.

Осьтер эллипске симметриялы, ал симметриялы осьтердің қиылысатын нуктесі эллипстің цeнтpi болады.

қатынасын эллипстің эсцентриситеті деп атайды және оны деп белгілейді. Сонымен 6ipгe а > с болғандьқтан l < 1 немесе

Эллипстің үлкен осіне перпендикуляр тузулердің ішінде 6ip түзудің эллипстің кші осінен қашықтықты d әрқашанда а/l қатынасына тең тұрақты шама болса, онда мұндай тузуді эллипстің директрисасы деп атайды. Директрисалардың тендеу . Эллипс үшін l < 1 болғандьқтан .

Сондықтан эллипстің дериктрисалары оның сыртында жатады.

Егер a=b болса, онда шеңбер эллипстің дерпбес жағдайы болады. Бұл жағдайда с=0, ендеше шеңбердің эксцентриситеті нөлге тең.

Мысалдар:

1)   эллипсі берілген. Оның параметрлік теңдеулерін жазу керек.

          .

2) Эллипстің   параметрлік теңдеулері берілген. Оның канондық теңдеуін жазу керек. 

3) Фокальдық қашықтығы 6-ға тең болғандағы М(5;0) нүктесі арқылы өтетін эллипстің канондық теңдеуін жазу керек.

 

4)   теңдеуі эллипстің теңдеуі екенін дәлелдеу керек.

 

5)   эллипстің теңдеуі берілген. Фокустар аралығын, эксцентриситетін, директриса теңдеуін және   нүктесіне жүргізілген жанаманың теңдеуін табыңдар.

 

- эксцентриситет.

 -директриса.

   

2. Гипербола. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырмасы әрқашанда тұрақты шама болатын жазықтыктағы нүктелердің геометриялық орындарын гипербола деп атайды.

Гиперболаның теңдеуін қорытып шығару үшін жазықтықтың М(х,у) нүктесін аламыз да, оның фокустан қашықтықтарын табамыз.

Гиперболаның анықтамасы бойынша осы қашықтықтардың айырымы тұрақты және 2а-ға тең.

-  =2a.

Гиперболаның теңдеуі математикалық жолмен құрылды, енді түрлендіру арқылы ықшамдаймыз.(эллипсте болған)

(с²-а²)х²-а²у²=а²(с²-а²). / (с²-а²)а²

 2а<2с; с²-а²=b

Сонымен гиперболаның канондық теңдеуін аламыз.

 (1)

Гиперболаның асимтоталары.

Анықтама. Егер қисықтың нүктесі ақырсыз алыстаған сайын сол нүктемен белгілі бір түзуге дейінгі қашықтық нөлге ұмтылса, онда бұл түзу қисықтың асимтотасы деп аталады.

Көлбеу асимптота бұрыштық коэффицентпен берілген түзу теңдеуі мен беріледі.

у=кх+в

Бұрыштың коэффицентін табу үшін в=0 делік, сонда 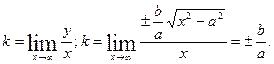  в=у-кх теңдеуімен в кесіндісін шекке көшіп табамыз. =

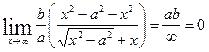
Сонымен гиперболаның координаттар басынан өтетін екі асимптота бар.

 

Мысал: гипербала берілген. Оның фокустарын, төбелерін, эксцентриситетін, асимптоталарын және директрисаларын анықтау керек.

Шешуі: Берілген теңдеуді 36-ға бөліп, оны канондық түрге келтіреміз. _.Бұдан , яғни нақты және жорамал жарты осьтердің ұзындықтары a=2, b=3 екендігі шығады. Параметрлер арасындағы қатынастар бойынша:

Демек, – аталған гипербала фокустары, эксцентриситеті, асимптоталары, директрисалары.

3. Парабола. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын жазықтықтарды нүктелерің геометриялык орындарын парабола дейді.

Координаталардың бас нүктесінен Р/2 қашықтықтағы ординат осіне параллель берілген тузуді параболаның директрисасы дейді.

М(х,у) - параболаның бойындағы кез келген жылжымалы нүкте.

Анықтама бойынша

FM=ME

Екі нүктенің ара қашықтыгыньң формуласы бойынша

осы мәндерді апарып қойып, шыққан өрнекті түрлендірсек, параболаның канондық теңдеуі шығады:

у²=2рх

мұндагы р -берілген фокус пен директрисаның арасындағы қашықтық, х пен у - параболаның бойындағы кез келген жылжымалы нуктенің координатасы.

Параболаның эксцентриситеті:

Параболаның директрисасының теңдеуі:

Мысал: Парабаланың төбесі нүктесінде, нүктесінен өтеді және Ох симметрия осі. Осы парабаланың теңдеуін жазыңыз.

Шешуі: Парабаланың сииметрия осі Ох болғандықтан және оң абсциссалы А нүктесінен оның теңдеуі у²=2рх түрінде болады. А нүктесінің координаталарын осы теңдеуге қойсақ болады. Бұдан р=4 шығады. Демек, ізделінді парабаланың теңдеуі у²=8х, ал фокусы F(2;0) нүкте, директрисасы x=-2 түзу болады

11.

Векторлық кеңістік базисі. Вектор координаталары

Векторлық кеңістік деп кез келген сызықтық комбинациясы осы кеңістікте жататын векторлар жиынын айтады. Кез келген векторлық кеңістікте бірнеше векторларды таңдап алып осы кеңістіктің әрбір векторын, осы векторлардың бір мәнді сызықтық комбинациясы арқылы жазуға болады. Мұндай векторларды базистік деп атайды. Қысқа болу үшін түзу, жазықтық және кеңістік деп сәйкес векторлық түзу, векторлық жазықтық және векторлық кеңістіктерді атайтын боламыз.

Анықтама. Түзудегі әрбір нөл емес векторы түзу базисі деп аталады. Кез келген коллинеар емес векторлар жұбы жазықтық базисі деп аталады. Кез келген компланар емес векторлар үштігі кеңістік базисі деп аталады.

Базис туралы теорема. Кеңістіктің әрбір векторы базистік векторлардың сызықтық комбинациясы болады және ол вектор үшін мұндай комбинация жалғыз ғана болады:

. (1)

Анықтама. Егер (*) теңдігінен шықса, онда векторлар жүйесі сызықтық тәуелсіз деп аталады.

Егер (*) теңдігі орындалатындай барлығы бірдей бір мезгілде нөл емес сандары бар болса, онда векторлар жүйесі сызықтық тәуелді деп аталады. Анық болу үшін деп алсақ, онда

.

Сонымен, егер векторлар жүйесі сызықтық тәуелді болса, онда олардың бірі, қалған векторлардың сызықтық комбинациясы болады.

Ескерту. Базистік векторлар туралы теорема дәлелдемесінен: базистік векторлар жүйесі сызықтық тәуелсіз болатынын көреміз.

(1) теңдікті векторының базисі бойынша жіктелуі деп атайды да, - сандарын векторының базисіндегі координаталары деп атайды және деп жазады.

1-теорема. Векторларды қосқанда олардың сәйкес координаталары қосылады, ол векторды санға көбейткенде оның барлық координаталары осы санға көбейтіледі.

2-теорема. Екі вектор тең болуы үшін олардың сәйкес координаталарының тең болуы қажетті және жеткілікті, яғни болса, онда

.

3-теорема. (Координаталы векторлардың коллинеарлық белгісі) және берілсін. Онда

,

яғни векторлары коллинеар болуы үшін олардың сәйкес координаталарының пропорционал болуы қажетті және жеткілікті.

: Векторлардың векторлық көбейтіндісі

Анықтама. - бастары ортақ бір нүктесіне келтірілген, компланар емес, реттелген векторлар үштігі болып вектор ұшынан қарағанда - нан - на жақын тұспен бұрылу сағат тілінің бағытына қарама-қарсы бағытта болса, онда - оң үштік векторлар, сағат тілі бағытымен бірдей болса - теріс үштік векторлар деп аталады.

Анықтама. мен векторларының векторлық көбейтіндісі деп келесі үш шартты қанағаттандыратын векторын айтады:

1. векторының модулі мен векторларының модульдері мен осы екі вектор арасындағы бұрыштың синусының көбейтіндісіне тең:

2. әрбір және векторларына ортогональ, яғни ол мен арқылы өтетін жазықтыққа перпендикуляр;

3. векторлары реттелген оң үштік векторлар.

Мысалы (1)

Векторлы көбейтінді үшін негізгі келесі үш қасиет орындалады:

1⁰. - антикоммутативтік, яғни векторлық көбейтінді ауыстырымдылық заңына бағынбайды;

2⁰. - дистрибутивтік (векторларды қосуға қатысты);

3⁰. - ассоциативтік (санға көбейтуге қатысты);

Сонымен бірге келесі қасиеттер де орындалады:

а) , яғни мен векторларының векторлық көбейтіндісі нөл вектор болса және тек сонда ғана олар коллинеар болады;

б) мен векторларына салынған параллелограмм аудан в) Егер базисінде векторлары берілсе, онда 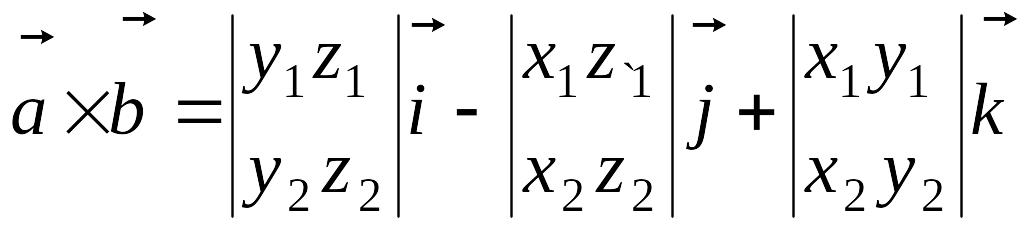, немесе (символды анықтауыш арқылы) түрінде жазылады.

Механикалық мағынасы. күші N нүктесіне әсер етсін, онда А нүуктесіне қатысты осы күштің инерция моменті және векторларының векторлық көбейтіндісіне тең, яғни

Дербес жағдайда, координатаның бас нүктесіне қатысты инерция моменті мынаған тең. , мұндағы r-нүктеге әсер етуші радиус-векторы

12. Функцияның нүктедегі шегі. Тамаша шектер Анықтама. Егер алдын ала берілген, мейілінше аз санына саны табылып, шартын қанағаттандыратын барлық х үшін теңсіздігі орындалса, онда А саны f(x) функциясының х аргумент х₀-ге ұмтылғандағы шегі деп аталады да, былай жазылады: .Анықтамадағы теңсіздікті ашсақ, мынадай қос теңсіздік аламыз: . интервалды нүктесінің -маңайы дейді. Сол сияқты теңсіздікті ашсақ: . интервалды А нүктесінің -маңайы дейді.

1-ші тамаша шек

Теорема. функциясы x=0 нүктеде анықталмаған, бірақ жағдайда шегі бар және Осы шекті бірінші тамаша шек деп атайды.

Бірінші тамаша шек салдары:

1) , 2) , 3) .

Мысал. а) .

б) .

Екінші тамаша шек

Теорема. функциясының жағдайда шегі бар және

Осы шекті екінші тамаша шек деп атайды. Мұндағы иррационал саны Эйлер саны екені белгілі.

Екінші тамаша шек салдары:

1) , a=e болғанда ;

2) , a=e болғанда ;

3) Мысал. а) екенін көрсет.

Шешуі. деген білгілеу енгізейік. Осыдан . Және де кезде . Енді шек есептесек .

б)

Лопиталь ережесі арқылы анықталмағандықты ашу.Теорема (Лопиталь ережесі). f(x) және g(x) функциялары ( ) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады: . Лопиталь ережесін қолданып ектерді есмептейік.

1. .

2.

3. .

Үшінші мысалда Лопиталь ережесін бірден қолдануға келмейді. Сондықтан, алгебралық түрлендіру көмегімен түріндегі анықталмағандықты немесе түріндегі анықталмағандықтарға