2 Пример решения типовых задач

1 Манометр на нагнетательном трубопроводе центробежного насоса (рис. 1), перекачивающего 8,4 м³ воды в минуту, показывает давление 3,8 кгс/см². Вакуумметр на всасывающем трубопроводе показывает вакуум 21 см. рт. ст. Расстояние по вертикали между местом присоединения манометра и местом присоединения вакуумметра 410 мм. Диаметр всасывающего трубопровода 350 мм, нагнетательного – 300 мм. Определить геометрический напор, развиваемый насосом.

Решение. Применяем формулу (1.10).

Скорость воды во всасывающем трубопроводе:

м/с

Скорость воды в нагнетательном трубопроводе:

м/с

Давление в нагнетательном трубопроводе (принимая атмосферное давление равным 760 мм. рт. ст.):

н/м²

Давление во всасывающем трубопроводе:

н/м²

Геометрический напор развиваемый насосом:

м вод.ст.

2 Поршневой насос, делающий 150 об/мин, должен перекачивать воду, нагретую до 60С. Предварительные расчеты показали, что затрата энергии на создание скорости, инерционные потери и гидравлические сопротивления всасывающей линии составляют в сумме 6,5 м. вод. ст. Среднее атмосферное давление в месте установки насоса 736 мм. рт. ст. На какой высоте над уровнем воды должен быть установлен насос?

Решение. Величина [формула (1.16)] в данном случае равняется:

м

где =2,02 м взято из табл. 2.

Следовательно, теоретическая высота всасывания не может быть больше 1,48 м. Практически, по данным табл. 1, высота всасывания в этом случае (n=150 об/мин) равна нулю, т.е. насос должен быть установлен ниже уровня жидкости (“под заливом”).

3 Поршневым насосом простого действия (рис. 2) с диаметром поршня 160 мм и ходом поршня 200 мм необходимо подавать 430 л/мин жидкости относительной плотности 0,93 из сборника в аппарат, давление в котором = 3,2 ат. Давление в сборнике атмосферное. Геометрическая высота подъема 19,5 м. Полная потеря геометрического напора во всасывающей линии 1,7 м, в нагнетательной – 8,6 м. Какое число оборотов надо дать насосу и какой мощности мотор установить, если принять коэффициент подачи насоса 0,85 и коэффициенты полезного действия: насоса 0,8, передачи и электромотора по 0,95?

Решение: Из формулы (1.17) находим:

В нашем случае:

об/мин

Геометрический напор, развиваемый насосом, определяем по формуле (1.10):

Мощность, потребляемую электродвигателем насоса, рассчитываем по формуле (1.12):

Где 0,72 – общий к.п.д. насосной установки:

В соответствии с данными табл. 1 необходимо установить ( с запасом на перегрузки) электромотор мощностью:

4 Поршневой насос двойного действия (рис. 8) подает 22,8 м³/час жидкости. Число оборотов насоса 65 об/мин, диаметр плунжера 125 мм, диаметр штока 35 мм, радиус кривошипа 136 мм. Определить коэффициент подачи насоса.

Решение. Объем, вытесняемый плунжером за один оборот:

где 0,272 м – длина хода плунжера, равная удвоенному радиусу кривошипа.

Рис. 8. Поршневой насос двойного действия

Теоретическая подача насоса при 65 об/мин:

Действительная подача:

Откуда коэффициент подачи:

5 Центробежный насос, делающий 1200 об/мин, показал при испытании следующие данные:

Q, л/сек	0	10,8	21,2	29,8	40,4	51,1
H*, м	23,5	25,8	25,4	22,1	17,3	11,9
N, кВт	5,16	7,87	10,1	11,3	12,0	18,5

Перекачивался раствор относительной плотности 1,12. Определить к.п.д. насоса для каждой производительности и построить графическую характеристику насоса.

Решение. К.п.д. насоса определяем из уравнения:

откуда

По этой формуле вычислены следующие значения к.п.д. насоса:

Q, л/сек	0	10,8	21,2	29,8	40,4	51,1
	0	0,39	0,587	0,643	0,637	0,36

Характеристика насоса представлена на рис. 9.

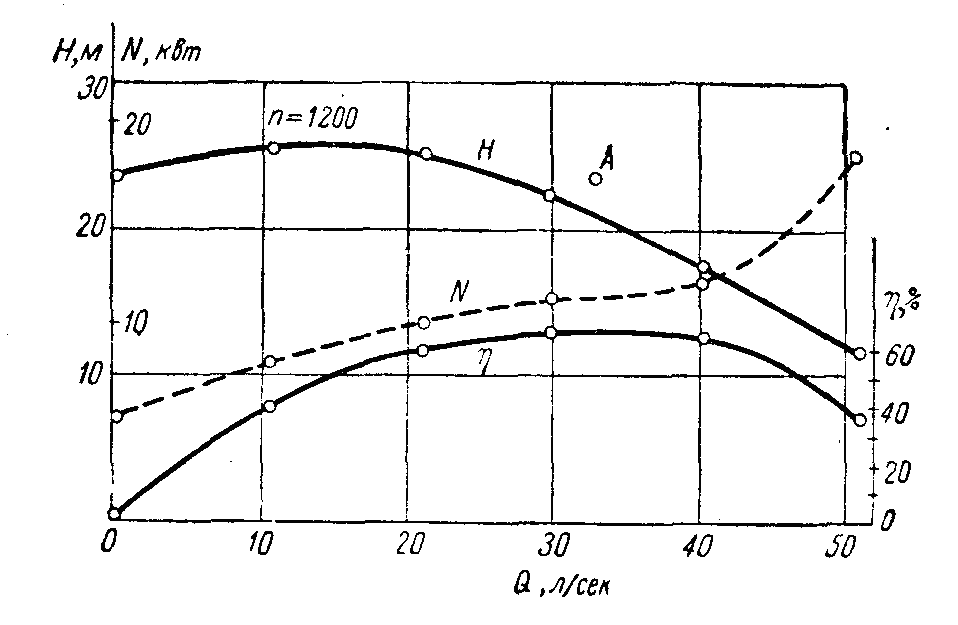
Рис. 9 Характеристики насоса.

6 Требуется подавать 115 м³/час раствора относительной плотности 1,12 из бака в аппарат на высоту 10,8 м, считая от уровня жидкости в баке. Давление в аппарате =0,4 ат, давление в баке атмосферное. Диаметр трубопровода 1404,5 мм, его расчетная длина (собственная плюс эквивалентная длина местных сопротивлений) 140 м. Можно ли применить центробежных насос примера задачи 5, если принять коэффициент трения в трубопроводе =0,03?

Решение. Определяем необходимый геометрический напор, который должен давать насос.

Скорость жидкости:

Скоростной напор:

Потеря напора на трение и местные сопротивления:

Требуемый полный геометрический напор насоса вычисляем по формуле (1.10):

Требуемая производительность насоса:

Обращаясь к рис.9, мы видим, что точка А с координатами Q=32 л/сек, Н*=23,8 м лежит выше кривой характеристики насоса и, следовательно, данный насос при n=1200 об/мин не сможет обеспечить требуемую производительность (при Н*=23,8 м насос может подавать только 26 л/сек). Однако если несколько увеличить число оборотов насоса, то он окажется пригодным. Пользуясь соотношениями (1.20)

и

можно подобрать необходимое новое число оборотов насоса n₂.

Если, например, взять n₂=1260 об/мин и пересчитать данные примера 5 по формулам (1.20) на это новое число оборотов, то получим следующие результаты (табл. 3).

Таблица 3

n1=1200	Q1, л/сек	21,2	29,8	40,4
	Н1, м	25,4	22,1	17,3
n2=1260	Q2, л/сек	22,3	31,3	42,5
	Н2, м	28,0	24,4	19,1

Вычертив по данным табл. 3 кривую характеристики насоса при n₂=1260 об/мин (рис 9), мы увидим, что при этом числе оборотов насос сможет обеспечить требуемые подачу (32 л/сек) и напор (23,8 м).

Мощность, потребляемую насосом при новом числе оборотов, определяем по формуле

Считая приближенно, что к.п.д. насоса не изменился^. Значение его берем по данным примера 5, в котором было найдено. Что для к.п.д. насоса

Мощность, потребляемая насосом при n₂=1260 об/мин: