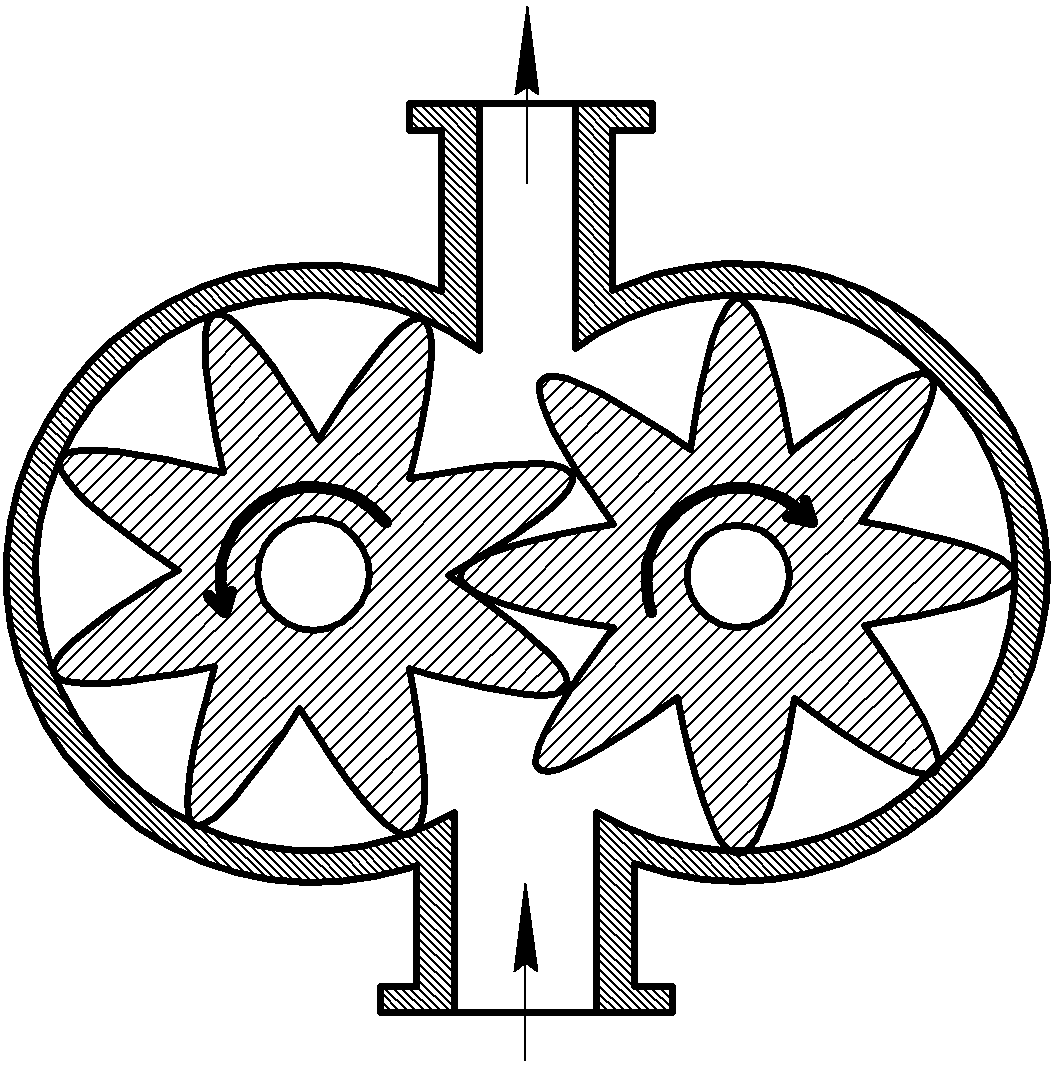МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
________________________________
Казанский государственный
энергетический университет
Ю.В. ВАНЬКОВ, А.Е. КОНДРАТЬЕВ, Р.Н. ВАЛИЕВ,
Ш.Г. ЗИГАНШИН
ТЕПЛОВЫЕ ДВИГАТЕЛИ И НАГНЕТАТЕЛИ
Казань 2007
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
__________________________________
Казанский государственный
энергетический университет
Ю.В. ВАНЬКОВ, А.Е. КОНДРАТЬЕВ, Р.Н. ВАЛИЕВ,
Ш.Г. ЗИГАНШИН
Утверждено
учебным управлением КГЭУ
в качестве учебного пособия
для студентов
ТЕПЛОВЫЕ ДВИГАТЕЛИ И НАГНЕТАТЕЛИ
УЧЕБНОЕ ПОСОБИЕ
для практических занятий
по курсу
ТЕПЛОВЫЕ ДВИГАТЕЛИ И НАГНЕТАТЕЛИ
Казань 2007
УДК 697.34
ББК
Ваньков Ю.В., Кондратьев А.Е., Валиев Р.Н., Зиганшин Ш.Г.
Тепловые двигатели и нагнетатели: Учеб. пособие для практических занятий. - Казань: Казан. гос. энерг. ун-т, 2007. - 52 с.
ISBN 0-00000-00-0
В учебном пособии для практических занятий рассмотрены основы расчета параметров и основных режимов работы насосов, компрессоров и вентиляторов различной конструкции. Приведены примеры решения задач по курсу «Тепловые двигатели и нагнетатели» и задачи для самостоятельных и классных занятий по каждому разделу дисциплины.
Предназначено для студентов старших курсов, проходящих обучение по направлению 140100 "Теплоэнергетика" для студентов очной, заочной и очно-заочной форм обучения.
_____________________________
Рецензенты
Д-р. техн. наук, проф. КГТУ Л.В.Горюнов
Д-р. техн. наук, проф.
Рекомендовано секцией РИС института теплоэнергетики
Председатель секции
ISBN 0-00000-00-0
|
Казанский государственный энергетический университет, 2007 Ваньков Ю.В., Кондратьев А.Е., Валиев Р.Н., Зиганшин Ш.Г., 2007 |
С О Д Е Р Ж А Н И Е
1. Основные теоретические сведения……………………………………….. |
5 |
2. Пример решения типовых задач…………………………………………... |
24 |
3. Контрольные задачи………………………………………………………. |
42 |
4. Исходные данные для расчета по вариантам ……………………………. |
46 |
1 Основные теоретические сведения
В современной технике машины для подачи жидкостей называют насосами, а машины для подачи газов подразделяются в зависимости от развиваемого ими давления на компрессоры, газодувки и вентиляторы.
Вентилятор
— машина, перемещающая газовую среду
при степени повышения давления
![]() до 1,15.
до 1,15.
Газодувка — машина, работающая при >1,15, но искусственно не охлаждаемая.
Компрессор сжимает газ при >1,15 и имеет искусственное (обычно водяное) охлаждение полостей, в которых происходит сжатие газа.
По принципу действия насосы и воздуходувные машины можно разделить на два класса: динамические и объемные.
В динамических насосах передача энергии потоку происходит под влиянием сил, действующих на жидкость в рабочих полостях, постоянно соединенных с входом и выходом насоса. Характерным представителем этого класса является центробежный насос.
В объемных насосах энергия передается жидкой среде в рабочих камерах, периодически изменяющих объем и попеременно сообщающихся с входом и выходом насоса. Для этого класса типичным является поршневой насос.
Основными величинами, характеризующими работу нагнетателей, являются подача, напор и давление, ими развиваемые. Энергия, сообщаемая потоку жидкости или газа машиной, вполне определяется этими величинами и плотностью подаваемой среды. Гидродинамическое и механическое совершенство машины характеризуется ее полным КПД.
Подача — количество жидкости (газа), перемещаемое машиной в единицу времени.
Если
подачу измеряют в единицах объема, то
ее называют объемной и обозначают
![]() .
.
В
системе СИ введена массовая
подача
![]() ,
кг/с, — масса
жидкости (газа), подаваемой машиной в
единицу времени. Очевидно, что
,
кг/с, — масса
жидкости (газа), подаваемой машиной в
единицу времени. Очевидно, что
![]() (1.1)
(1.1)
где
![]() - плотность системы, кг/м3;
- плотность системы, кг/м3;
- объемная подача, м3/с.
При отсутствии утечек массовая подача одинакова для всех сечений проточной полости машины независимо от рода подаваемой среды. Объемная подача практически одинакова по всей длине проточной полости только в насосах и приблизительно одинакова в вентиляторах. В компрессорах вследствие существенного повышения давления происходит уменьшение удельного объема газа и объемная подача по длине проточной полости падает.
Давление нагнетателя Р, Па, определяется как разница давлений жидкости на выходе и входе нагнетателя. Давление является энергетической характеристикой потока и показывает, насколько увеличивает нагнетатель энергию потока. В этом контексте давление Р следует понимать не как силу F, действующую на единицу площади S, а как энергию E, приходящуюся на единицу объема V жидкости или газа (Па = Н/м2 = (Н·м)/(м2·м) = Дж/м3):
Р = F/S = E/V (1.2)
Под полным давлением подразумевается сумма:
![]() ,
(1.3)
,
(1.3)
где
![]() - статическое давление;
- статическое давление;
![]() - динамическое
давление.
- динамическое
давление.
Величина
![]() по сравнению с первыми двумя значительно
мала, поэтому ей можно пренебречь.
по сравнению с первыми двумя значительно
мала, поэтому ей можно пренебречь.
Динамическое
давление
![]() рассматривается как кинетическая
энергия, отнесенная к 1 м3,
и имеет вид:
рассматривается как кинетическая
энергия, отнесенная к 1 м3,
и имеет вид:
![]() (1.4)
(1.4)
Статическое
давление определяется как разность
между абсолютным статическим
![]() и атмосферным давлением
и атмосферным давлением
![]() :
:
![]()
Необходимо отметить, что дифференциальный манометр, подключенный к воздуховоду, измеряет непосредственно .
Напор, развиваемый
насосом, определяют как разность удельных
энергий после
![]() и до
и до
![]() насоса:
насоса:
![]() .
.
Отсюда следует, что напор является удельной работой и в системе СИ и имеет размерность дж/кг. В системе MKS напор измеряется в метрах столба жидкости и связан отношением:
![]() .
(1.5)
.
(1.5)
Величина
![]() называется геометрическим напором и
далее под словом «напор» будем понимать
высоту столба жидкости, создающего
определенное значение давления, то есть
ту высоту, на которую может быть поднята
жидкость под действием данной удельной
работой. Связь между напором и давлением
имеет вид:
называется геометрическим напором и
далее под словом «напор» будем понимать
высоту столба жидкости, создающего
определенное значение давления, то есть
ту высоту, на которую может быть поднята
жидкость под действием данной удельной
работой. Связь между напором и давлением
имеет вид:
Р = ρ·g·Н*, (1.6)
где ρ - плотность жидкости, кг/м3;
g - ускорение свободного падения (g = 9,81 м/с2).
![]()
Подача насоса (вентилятора, компрессора) зависит от размеров и скоростей движения его рабочих органов и свойств трубопроводной системы, в которую он включен.
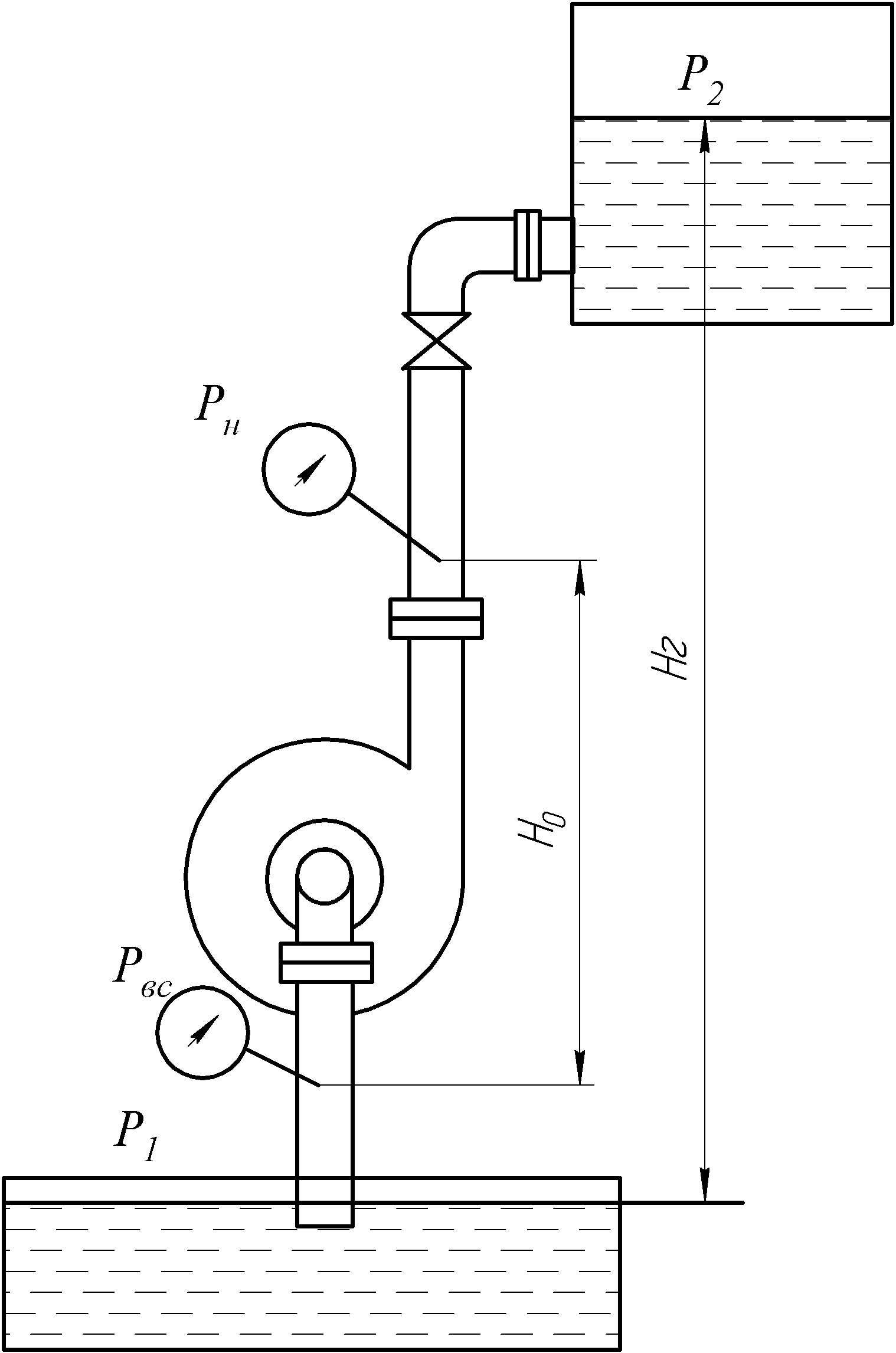
Работа насоса, присоединенного к системе водопроводов, находится в зависимости от гидравлических свойств этой системы, называемой сетью. Рассмотрим условия работы машины на примере насосной установки (рис.1), полагая систему устойчивой.
Первое условие связи насоса с трубопроводной системой следует из уравнения неразрывности и заключается в равенстве массовых подач, проходящих через насос и присоединенные к нему всасывающий и напорный трубопроводы:
Для
несжимаемой жидкости
|
Рис.1. Центробежный насос |
![]() (1.8)
(1.8)
Полный напор, развиваемый центробежным насосом, определяется из уравнения:
![]() ,
(1.9)
,
(1.9)
или с учетом (1.5)
![]() ,
(1.10)
,
(1.10)
где - полный геометрический напор, развиваемый насосом, м. вод. ст.;
![]() и
и
![]() - давление на поверхности жидкости в
пространстве нагнетателя и в пространстве
всасывания, н/м2;
- давление на поверхности жидкости в
пространстве нагнетателя и в пространстве
всасывания, н/м2;
![]() - плотность
перекачиваемой жидкости, кг/м3;
- плотность
перекачиваемой жидкости, кг/м3;
![]() - геометрическая
высота подъема жидкости, м;
- геометрическая
высота подъема жидкости, м;
![]() - напор, затрачиваемый
на создание скорости и на преодоление
силы трения и всех местных сопротивлений
во всасывающей и нагнетательной линиях,
м;
- напор, затрачиваемый
на создание скорости и на преодоление
силы трения и всех местных сопротивлений
во всасывающей и нагнетательной линиях,
м;
g=9,81 м/сек2 – ускорение свободного падения.
Также полный геометрический напор можно рассчитать при известных скоростях жидкости на входе и выходе из насоса по формуле:
![]() ,
(1.11)
,
(1.11)
где
![]() и
и
![]() - давление в нагнетательном и всасывающем
трубопроводах насоса соответственно,
н/м2;
- давление в нагнетательном и всасывающем
трубопроводах насоса соответственно,
н/м2;
![]() - вертикальное
расстояние между точками измерения
давления, м;
- вертикальное
расстояние между точками измерения
давления, м;
![]() и
и
![]() - скорость жидкости в нагнетательном и
всасывающем трубопроводах насоса
соответственно, м/сек.
- скорость жидкости в нагнетательном и
всасывающем трубопроводах насоса
соответственно, м/сек.
Полезная мощность насоса – это работа, сообщаемая машиной в секунду подаваемой среде и определяется соотношением:
![]() ,
(1.12)
,
(1.12)
где Q – объемная производительность, м3/сек;
g=9,81 м/сек2 – ускорение свободного падения.
![]() - плотность
перекачиваемой жидкости, кг/м3;
- плотность
перекачиваемой жидкости, кг/м3;
- полный геометрический напор, развиваемый насосом, м. вод. ст.;
![]() - полный КПД насоса.
- полный КПД насоса.
Эффективность использования насосом энергии, к нему подводимой, оценивают КПД насоса - отношением полезной мощности к потребляемой мощности насоса:
![]() ,
(1.13)
,
(1.13)
В системах, состоящих из нескольких элементов, полный КПД оценивается путем перемножения КПД каждого отдельного элемента, например:
![]() ,
(1.14)
,
(1.14)
где n – количество элементов системы.
Учитывая возможные
перегрузки системы, запланированные
потери и возможность повышения надежности,
ввели коэффициент запаса мощности
![]() :
:
![]() ,
(1.15)
,
(1.15)
где
![]() - мощность установки.
- мощность установки.
, кВт |
|
Коэффициент запаса мощности выбирается в зависимости от величины мощности в соответствии с приведенной таблицей. |
менее 1 |
2 – 1,5 |
|
1 – 5 |
1,5 – 1,2 |
|
5 – 50 |
1,2 – 1,15 |
|
более 50 |
1,1 |
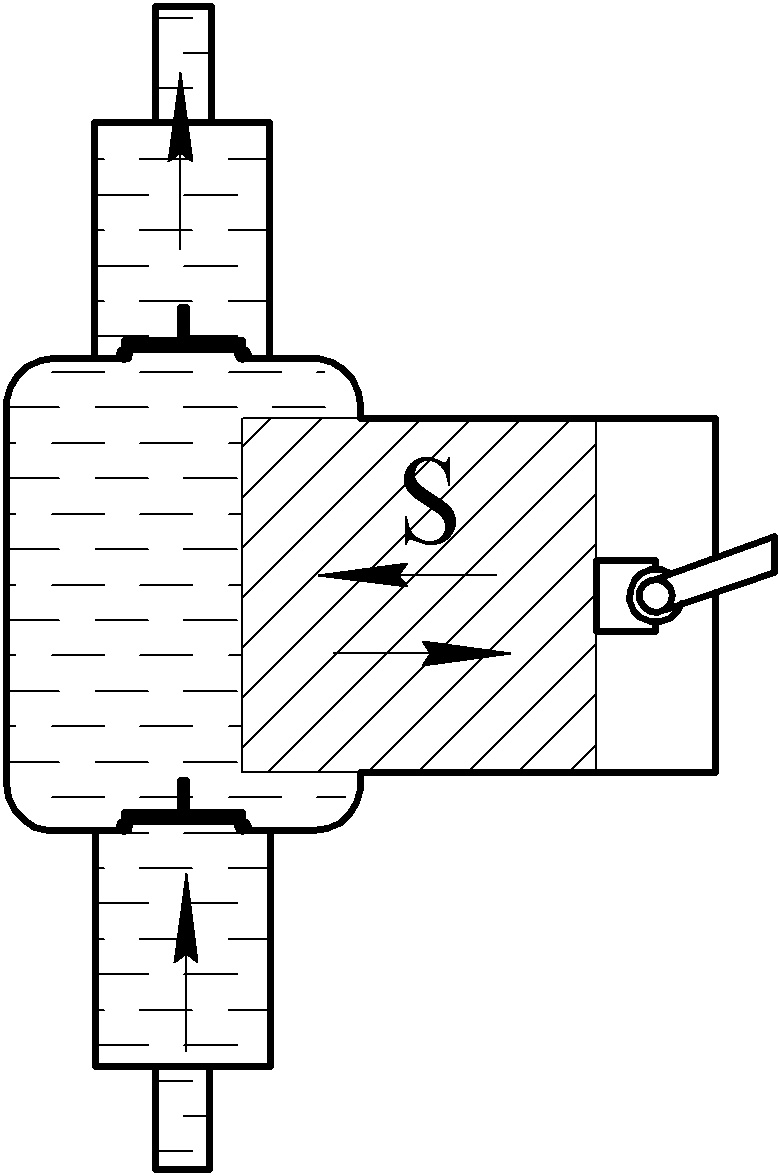
Теоретическая высота всасывания поршневого насоса (рис. 2) определяется выражением:
![]() ,
(1.16)
,
(1.16)
Рис. 2. Поршневой насос |
где
|
Атмосферное давление зависит от высоты места установки насоса над уровнем моря и находится из таблицы:
Таблица 1
Высота над уровнем моря, м |
-600 |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
1500 |
Атмосферное давление , м.вод. ст. |
11,3 |
10,3 |
10,2 |
10,1 |
10,0 |
9,8 |
9,7 |
9,6 |
9,5 |
9,4 |
9,3 |
9,2 |
8,6 |
Давление насыщенного пара всасываемой жидкости определяется ее температурой. Для воды зависимость величины от температуры представлена в таблице:
Таблица 2
Температура, °С |
5 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
Давление насыщенного пара , м.вод. ст. |
0,09 |
0,12 |
0,24 |
0,43 |
0,75 |
1,25 |
2,02 |
3,17 |
4,82 |
7,14 |
10,33 |
Подача , м3/сек поршневого насоса простого действия (рис. 2) определяется:
![]() ,
1.17
,
1.17
.где
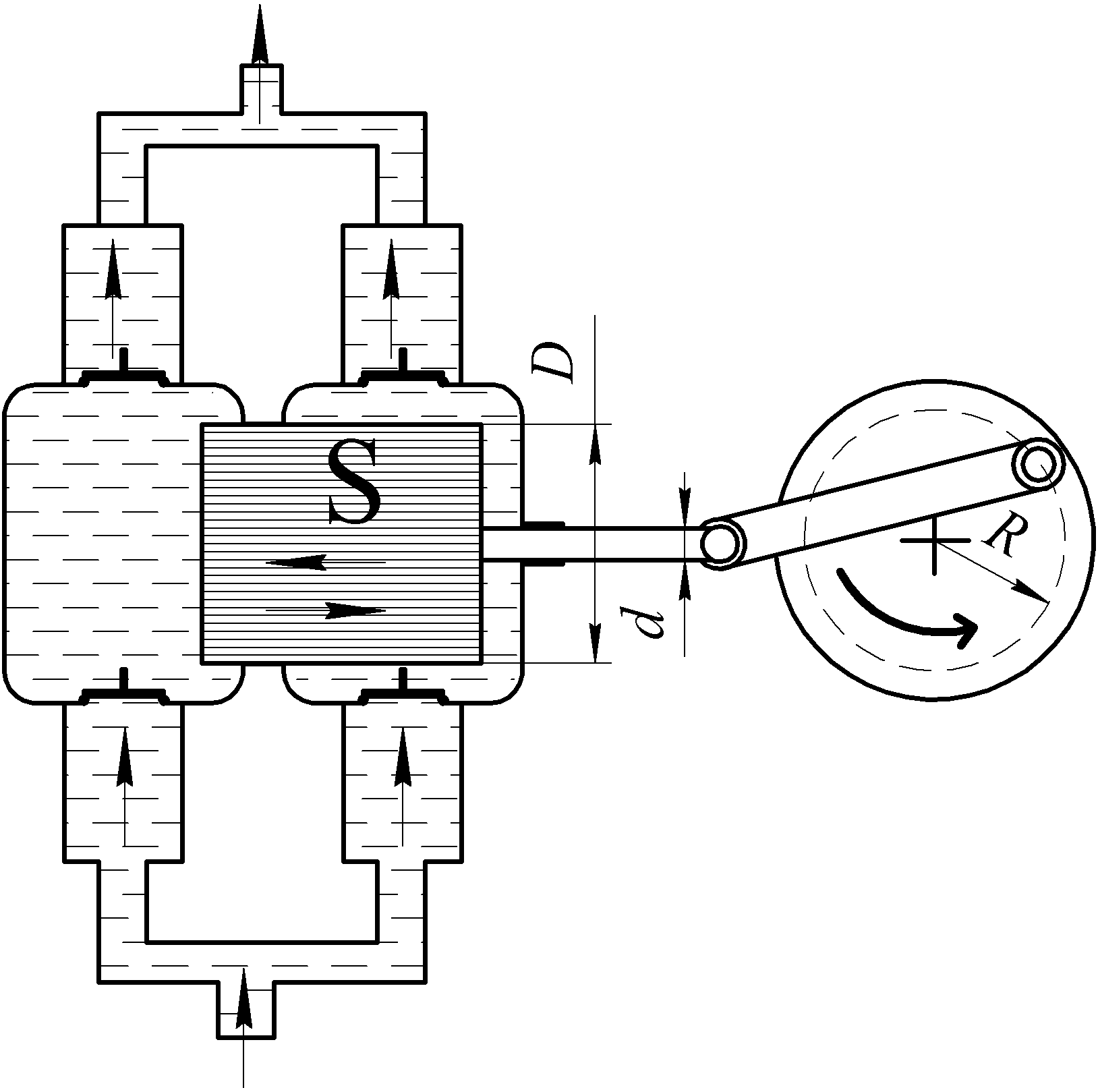
Подача поршневого насоса двойного действия (рис. 3) определяется:
|
Рис. 3. Двухтактный поршневой насос
|
где
![]() - площадь поперечного сечения, м2.
- площадь поперечного сечения, м2.
Здесь величина хода поршня связана с радиусом кривошипа соотношением:
![]() (1.19)
(1.19)
Напор, производительность
и мощность центробежного насоса при
изменении числа оборотов
связаны соотношениями. При изменении
числа оборотов от
![]() до
до
![]() центробежного насоса подача
,
геометрический напор
и мощность
центробежного насоса подача
,
геометрический напор
и мощность
![]() находятся в зависимости:
находятся в зависимости:
![]() ;
;
 ;
;
 ,
(1.20)
,
(1.20)
Высота всасывания
![]() (м) центробежного насоса рассчитывается
по формуле:
(м) центробежного насоса рассчитывается
по формуле:
![]() ,
(1.21)
,
(1.21)
где - атмосферное давление;
- давление насыщенного всасываемого пара;
![]() - гидравлическое
сопротивление всасывающей линии, включая
затрату энергии на сообщение скорости
потоку жидкости;
- гидравлическое
сопротивление всасывающей линии, включая
затрату энергии на сообщение скорости
потоку жидкости;
![]() - кавитационная
поправка (уменьшение высоты всасывания
во избежание кавитации), зависящая от
производительности насоса
(м3/сек)
и числа оборотов
(об/мин):
- кавитационная
поправка (уменьшение высоты всасывания
во избежание кавитации), зависящая от
производительности насоса
(м3/сек)
и числа оборотов
(об/мин):
![]() (1.22)
(1.22)
Величины , , и выражены в метрах столба перекачиваемой жидкости.
Физические явления, протекающие в геометрически подобных пространствах, называются подобными, если в соответственных точках этих пространств сходственные физические величины находятся в постоянных соотношениях.
В общем виде работа центробежного насоса может быть описана обобщенными безразмерными уравнениями, включающими критерии подобия. Условия геометрического подобия заключаются в равенстве сходственных углов и постоянстве отношений сходственных геометрических величин, тогда для различных диаметров колеса справедливо соотношение:
![]() ,
(1.23)
,
(1.23)
где
![]() - диаметры колес а и
b
на входе;
- диаметры колес а и
b
на входе;
![]() - диаметры колес
а и
b
на выходе;
- диаметры колес
а и
b
на выходе;
![]() - коэффициент
геометрического подобия.
- коэффициент
геометрического подобия.
Кинематическое подобие состоит в постоянстве отношений скоростей в сходственных точках геометрически подобных машин и равенстве сходственных углов параллелограммов скоростей:
![]() - угол между
абсолютной и окружной скоростями на
входе;
- угол между
абсолютной и окружной скоростями на
входе;
![]() - угол между
абсолютной и окружной скоростями на
выходе.
- угол между
абсолютной и окружной скоростями на
выходе.
Тогда верно соотношение:
![]() (1.24)
(1.24)
где
![]() - коэффициент кинематического подобия.
- коэффициент кинематического подобия.
Динамическое подобие выражается постоянством отношений сил одинаковой природы, действующих в сходственных точках геометрически и кинематически подобных машин:
![]() ,
(1.25)
,
(1.25)
где
![]() - коэффициент динамического подобия.
- коэффициент динамического подобия.
Критерий мощности определяется следующей безразмерной величиной:
![]() .
(1.26)
.
(1.26)
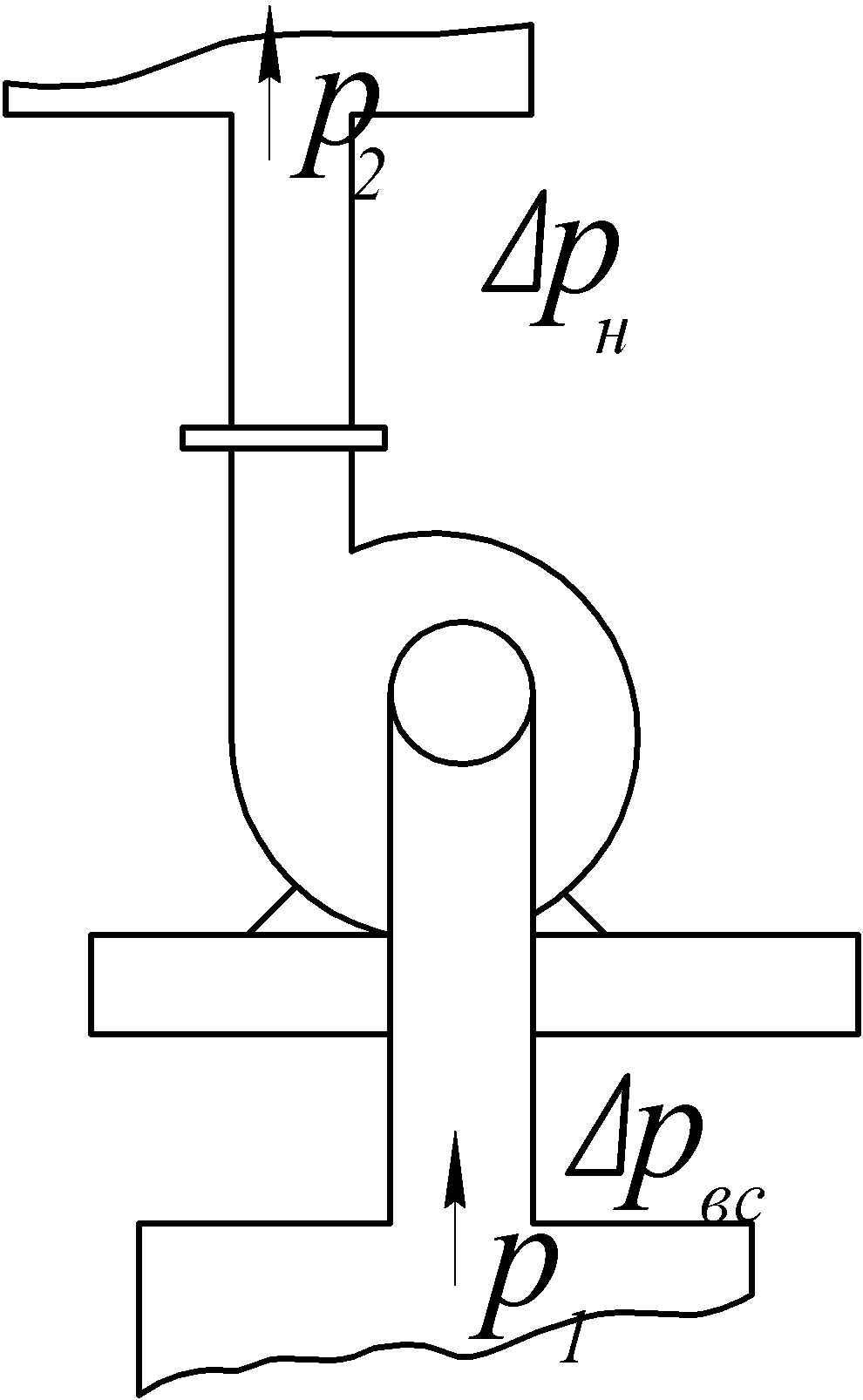
Для расчета давления, создаваемого центробежным вентилятором (рис.4) при подаче им воздуха, применяются следующие уравнения:
![]() , (1.27)
, (1.27)
![]() ,
(1.28)
,
(1.28)
где
и - давление забираемого и подаваемого воздуха, н/м2;
- плотность воздуха, кг/м2. |
Рис. 4. Схема центробежного вентилятора |
Если вентилятор подает не воздух, а другой газ, отличающейся по плотности от окружающего воздуха, то уравнение (1.27) примет вид:
![]() , (1.29)
, (1.29)
![]() ,
(1.30)
,
(1.30)
где
![]() - разность высот мест нагнетания и
всасывания, м.
- разность высот мест нагнетания и
всасывания, м.
Мощность, расходуемая вентиляторной установкой:
![]() ,
(1.31)
,
(1.31)
где Q – объемная производительность, м3/сек;
- повышение давления, создаваемое установкой, н/м2;
![]() - полный КПД
вентилятора.
- полный КПД
вентилятора.
Зависимость между старыми и новыми параметрами центробежного вентилятора, так же, как и центробежного насоса, связана с измерением числа оборотов вращения и определяется по формулам (1.20). Графически примерная характеристика центробежного вентилятора при различном числе оборотов представлена на рис. 5.
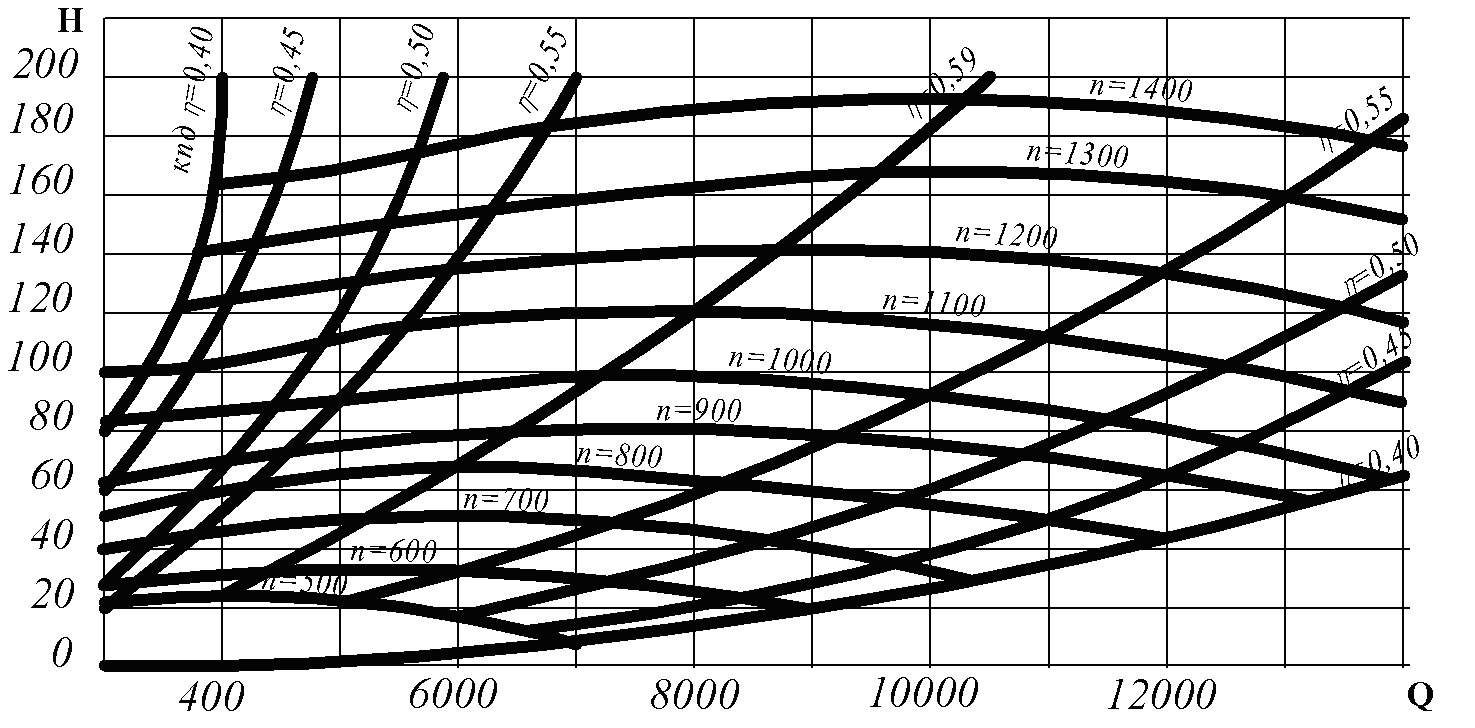
Рис.5. Характеристики центробежного насоса
Для одноступенчатого
компрессора теоретическая величина
работы
![]() (Дж/кг) при адиабатическом сжатии 1
кг газа определяется по формуле:
(Дж/кг) при адиабатическом сжатии 1
кг газа определяется по формуле:
 ,
(1.32)
,
(1.32)
или
![]() .
(1.33)
.
(1.33)
Температура газа в конце процесса адиабатического сжатия определяется по формуле:
 ,
(1.34)
,
(1.34)
где
![]() - показатель адиабаты, равный отношению
- показатель адиабаты, равный отношению
![]() ;
;
и - начальное и конечное давление газа, н/м2;
![]() - удельный объем
газа при начальных условиях, т.е. при
давлении
и температуре
- удельный объем
газа при начальных условиях, т.е. при
давлении
и температуре
![]() ,
м3/кг;
,
м3/кг;
![]() и
и
![]() - начальная и конечная энтальпия
(теплосодержание) газа, Дж/кг;
- начальная и конечная энтальпия
(теплосодержание) газа, Дж/кг;
![]() - газовая постоянная,
равная
- газовая постоянная,
равная
![]() ,
Дж/кг град;
,
Дж/кг град;
- молекулярная масса газа.
Мощность
(кВт), потребляемая двигателем
одноступенчатого компрессора, сжимающего
![]() кг газа в час от начального давления
до конечного давления
кг газа в час от начального давления
до конечного давления
![]() ,
рассчитывается по формуле:
,
рассчитывается по формуле:
![]() ,
(1.35)
,
(1.35)
где - общий к.п.д.
Производительность , м3/сек поршневого компрессора простого действия определяется по формуле:
![]() ,
(1.36)
,
(1.36)
где
![]() - коэффициент подачи, безразмерный;
- коэффициент подачи, безразмерный;
– площадь поршня, м2;
– длина хода поршня, м;
– частота вращения привода, об/мин.
Коэффициент подачи
![]() :
:
![]() ,
(1.37)
,
(1.37)
Здесь
![]() - объемный к.п.д. компрессора, равный:
- объемный к.п.д. компрессора, равный:
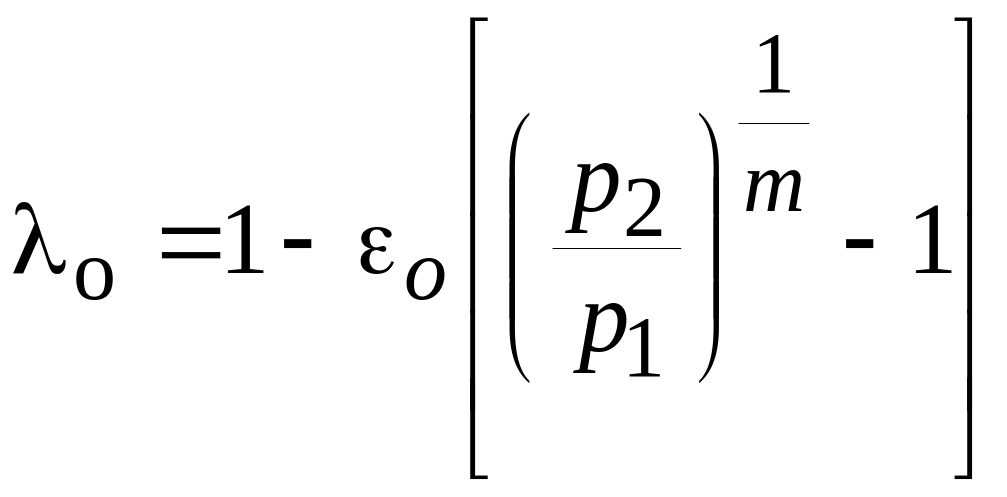 ,
(1.38)
,
(1.38)
где
![]() - отношение объема вредного пространства
цилиндра к объему, создаваемого поршнем;
- отношение объема вредного пространства
цилиндра к объему, создаваемого поршнем;
![]() - показатель
политропы расширения газа, оставшегося
во вредном пространстве.
- показатель
политропы расширения газа, оставшегося
во вредном пространстве.
Теоретическая
величина работы
(Дж/кг), затрачиваемой многоступенчатым
компрессором при адиабатическом сжатии
1 кг газа от начального давления
до конечного давления
![]() ,
определяется по формуле:
,
определяется по формуле:
 .
(1.39)
.
(1.39)
Или по формуле:
![]() ,
(1.40)
,
(1.40)
где - число ступеней сжатия;
![]() - разности энтальпий
газа для 1, 2, … ступени (формула 1.33).
- разности энтальпий
газа для 1, 2, … ступени (формула 1.33).
Потребляемая многоступенчатым компрессором мощность рассчитывается по формуле (1.35). Для воздушных компрессоров иногда пользуются также приближенным уравнением , кВт:
 ,
(1.41)
,
(1.41)
где 1,69 – установленный практически коэффициент, учитывающий отличие действительного процесса сжатия воздуха от изотермического.
Производительность многоступенчатого поршневого компрессора определяется производительностью первой ступени.
Пренебрегая потерей давления между ступенями, приближенно число ступеней сжатия находят из уравнения:
![]() ,
(1.42)
,
(1.42)
откуда
![]() ,
(1.43)
,
(1.43)
где
![]() - степень сжатия в одной ступени.
- степень сжатия в одной ступени.
Главными рабочими деталями шестеренного насоса являются две одинаковые шестерни (рис. 6), находящиеся в зацеплении, помещенные в плотно охватывающий их корпус. Ведущая шестерня получает вращение от двигателя.
Рис. 6. Шестеренчатый насос |
Производительность шестеренчатого насоса определяется:
где
– площадь сечения зуба, ограниченная внешней окружностью соседней шестерни;
|
– число зубьев в шестерне;
– число оборотов в минуту.
Производительность шестеренчатого насоса определяется:
![]() ,
(1.44)
,
(1.44)
где - коэффициент подачи;
– площадь сечения зуба, ограниченная внешней окружностью соседней шестерни;
– ширина зуба;
– число зубьев в шестерне;
– число оборотов в минуту.
Производительность насоса исчисляется в м3/час, а частота вращения – об/мин, поэтому в знаменателе стоит число 60.
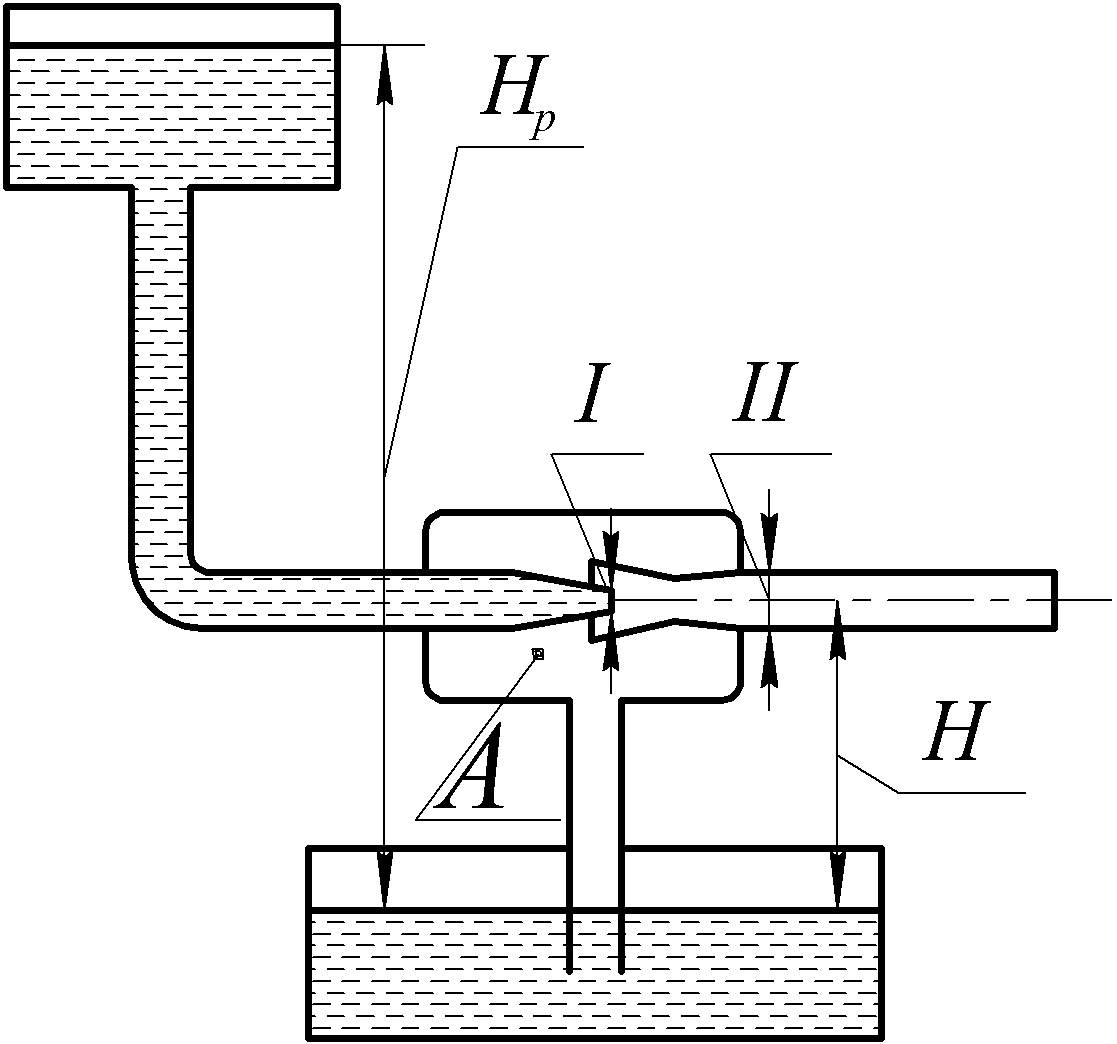
В промышленности для перемещения жидкостей и газов находят применение насосы струйного типа. Схема такого насоса приведена на рисунке 7.
Рис. 7. Водоструйный насос |
Для сечений струи I и II справедливо уравнение Бернулли:
где
и - давление в сечениях I и II, н/м2; |
![]() и
и
![]() - скорость течения жидкости в сечениях
I и II,
м/сек;
- скорость течения жидкости в сечениях
I и II,
м/сек;
- плотность жидкости, кг/м3.
Скорость течения жидкости зависит от значений сечений I и II и определяется, как:
![]() .
(1.46)
.
(1.46)