41.Тритемиус шифрінің математикалық моделі

Тритемиус ауыстыру шифрын алу үшін әдетте алфавиттің әpiптepi мен кілттік сөз (немесе сөздер тіркестігі) жазбасына арналған кесте қолданылған. Кестеге алдымен кілттік сөз жазылып, қайталанатын әpіптері алынып тасталады. Содан кейін бұл кесте алфавиттің кілтке кірмей қалған әріптермен реттелген түрде толықтырылады.

Қазақ алфавиті үшін шифрлайтын кестенің өлшемі 6x7 болады. Кілт ретінде АЛГОРИТМ сөзін алайық. Осындай кілтпен шифрлайтын кесте 3-суретте көрсетілген.

Тритемиус шифрінің математикалық моделі

Тритемиус шифріне арналған шифрлау теңдеуі мына түрдегідей болады:

Мұндағы L- шифрленген әріптің алфавиттегі номері; m —шифрленетін әріптің алфавиттегі орны; k —жылжу қадамы; N — алфавиттегі әріп саны.

Жылжу қадамын k есептейтін өрнек:

мұндағы p — берілген сөздегі әріптің позициясы; A, B, C — кілттер.

Мысал

1. Әріптің алфавиттегі кодын анықтаймыз

2. Жылжу қадамын есептейміз.

3. Келесі теңдеуді пайдаланып шифрленген әріптің кодын анықтаймыз: 

4. Сәйкесінше алдыдағы өрнек бойынша келесі әріптердің кодын табамыз

5. Тексттегі әріптер біткенше осы процедура қайталанады.

Егер L есептеу барысында k мәні теріс болса ,оған сәйкесінше N қосып отырамыз,нәтижеміз оң болғанша.Содан кейін бөлудегі қалдықты аламыз.

42.Криптографиялық кілттермен басқару. Кілттерді генерациялау (кездейсоқ табу).

Криптоанализ - ақпаратты кілтсіз кері шифрлау мәселесімен айналысады. Криптожүйеге сәтті жүргізілген криптоаналитикалық зерттеулер негізінде хабардың бастапқы ашық мәтінімен қатар оның кілтін де ашуға мүмкін болады. Криптоаналитиқ шифрланған хабарды, немесе кілтті, немесе екеуін де оқуға мүмкіндік беретін криптожүйенің осал жерлерін ідеумен шұғылданады. Шифрлау алгоритмі, сондай-ақ, алуан түрлі кіттердің, ашық және шифрланған мәтіндердің жиынтығын криптожүйе деп айтады.

Қазіргі криптография- 4 ірі бөлімнен тұрады:

1. Симметриялық криптожүйе

2. Ашық кілтті криптожүйе

3. Электрондық қол жүйесі

4. Кілт арқылы басқару

Криптожүйелер симметриялық және ашық кілтті жүйеге бөлінеді. Симметриялық криптожүйеде шифрлауға да, кері шифрлауға да бір ғана кілт қолданылады. Ашық кілтті жүйеде бір-бірінен математикалық байланыста болатын екі-ашық және жабық кілт пайдаланылады. Ақпарат барлық адамның қолы жететін ашық кілтпен шифрленеді де, ал оны ашу ақпаратты алушыға ғана белгілі жабық кілтпен ашылады.

Кілттерді бөлу және кілттерді басқару –пайдаланушылар арасындағы кілттерді бөлу және жасаудан тұратын ақпаратты өңдеу жүйесінің жұмысына жатады.

Кілтті генерациялау (кездейсоқ таңдау)

1-қадам. Екі үлкен p және q жай сандары таңдалады.

2-қадам. N = pq табылады

3-қадам. (N) = (p-1) (q-1) есептеледі

4-қадам. Кез-келген e (e<n) саны таңдалады, e және (N) өзара жай сандар болуы тиіс.

5-қадам. de mod m = 1 болатындай d табылады

(e,n) – екі саны ашық кілт ретінде таратылады. d саны құпия сақталады және (e,n) көмегімен шифрленген мәтінді ашуға пайдаланылатын жабық кілт болып табылады.

Шифрлеу

C = P^e mod n

Кері шифрлеу

P = C^d mod n

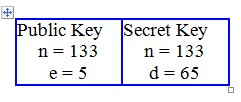
Кілтті генерациялау (кездейсоқ таңдау) мысалы

1) p = 7, q = 19

2) N = pq

N = 7 * 19  = 133

3) (N) = (p-1) (q-1)

(N) = (7 - 1)(19 - 1)  = 6 * 18  = 108

4) (N) – мен өзара жай болатындай кез-келген e (e< N ) таңдалады.

Яғни ЕҮОБ(e, (N)) 1-ге тең болуы керек. ЕҮОБ(e, (N)) табу үшін Евклид әдісін қолданамыз. Төменде осы процедуралар келтірілген.

e = 2 => ЕҮОБ(e, (N)) = ЕҮОБ(e, 108) = 2 (жоқ)

e = 3 => ЕҮОБ(e, (N)) =ЕҮОБ(e, 108) = 3 (жоқ)

e = 4 => ЕҮОБ(e, (N)) =ЕҮОБ(e, 108) = 4(жоқ) e = 5 => ЕҮОБ(e, (N)) =ЕҮОБ(e, 108) = 1 (иә!)

5) d-ны, de mod m = 1 болатындай табамыз

de = 1 + nm, мұндағы n-кез-келген сан. Бұл жолды ары қарай d = (1 + nm) /e деп жаза аламыз. N-нің орнына нөлден бастап сандарды қоя отырып d –ны табатынымыз келесідей:

n = 0 => d = 1 / 5 (жоқ)

n = 1 => d = 109 / 5 (жоқ) n = 2 => d = 217 / 5(жоқ) n = 3 => d = 325 / 5 = 65 (иә!)

Үлкен сандармен жұмыс жасағанда Евклид әдісі қолданылады.