2.7. Послідовне сполучення в колі синусоїдного струму

Нехай на вході електричного кола (рис. 2.7, а) прикладена синусоїдна напруга:

(2.34)

Диференціальне рівняння кола:

(2.35)

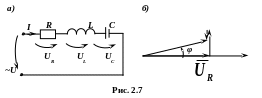
Струм усталеного режиму в колі також синусоїдний і змінюється з тією ж частотою, що й вхідна напруга :

, (2.36)

де – кут зсуву фаз між струмом і напругою на вході кола.

На основі рівняння (2.35) будуємо векторну діаграму кола для діючих значень струму і напруг (рис. 2.7, б). Вектор напруги на резистивному опорі збігається за напрямком із вектором струму , вектор напруги на індуктивності випереджує вектор струму на кут , а вектор напруги на ємності відстає від вектора струму на кут . Отже, між векторами та утворюється кут, що дорівнює . Вектор напруги , прикладеної до кола, дорівнює сумі векторів напруг на окремих його ділянках:

, (2.35, а)

а його величина

.

Завдання полягає у відшуканні величини і при відомих величинах і .

При дослідженні усталеного режиму величина або може бути вибрана довільно. Так як спільним у даному випадку для всіх ділянок є струм, то доцільно вибрати його початкову фазу , тобто .

Тоді

(2.37)

. (2.38)

Підставивши вирази (2.37) і (2.38) у рівняння (2.35), одержимо

(2.39)

Рівність (2.39) справедлива для довільного моменту часу . Зокрема, поклавши і , одержимо

; (2.40)

(2.41)

Піднесемо рівності (2.40) і (2.41) до квадрату і додамо їх ліві і праві частини

або .

Звідси одержимо зв’язок між амплітудами струму і напруги

. (2.42)

Розділивши на ліву і праву частини рівності, одержимо зв’язок між їх діючими значеннями, тобто закон Ома в класичній формі

. (2.43)

Поділивши (2.41) на (2.40), одержимо

,

звідки (2.44)

У виразах (2.42) і (2.43) величина знаменника має розмірність опору. ЇЇ позначають літерою і називають повним опором кола

. (2.45)

При збільшенні частоти індуктивний опір збільшується за рахунок збільшення ЕРС, самоіндукції , а ємнісний опір зменшується, так як збільшується струм зміщення, який пропорційний – швидкості зміни напруги на обкладинках конденсатора.

Напруга на активному опорі

за фазою співпадає зі струмом у колі.

Напруга на індуктивності

випереджує струм на кут .

Напруга на ємності

відстає від струму на кут .

Додаючи геометрично вектори напруг , , , одержимо вектор напруги на вході кола, який зміщений відносно вектора струму на кут .

Так як напруги і зсунуті одна відносно одної на кут , то не можна повний опір визначити шляхом арифметичного додавання величин опорів і , а слід визначити за формулою:

. (2.46)

Розглянемо тепер зсув фаз між напругою та струмом на вході кола.

Струм співпадає за фазою з прикладеною напругою тільки при , тобто при відсутності в колі реактивних опорів, або при їх взаємній компенсації. Останнє має місце при резонансі напруг.

При векторна сума і вектори та співпадають за напрямком.

Якщо , то і . Струм відстає від прикладеної напруги на кут (кут зсуву фаз).

Якщо , то і . Стум випереджує за фазою напругу на кут .

Таким чином, границі зміни кута зсуву фаз: .