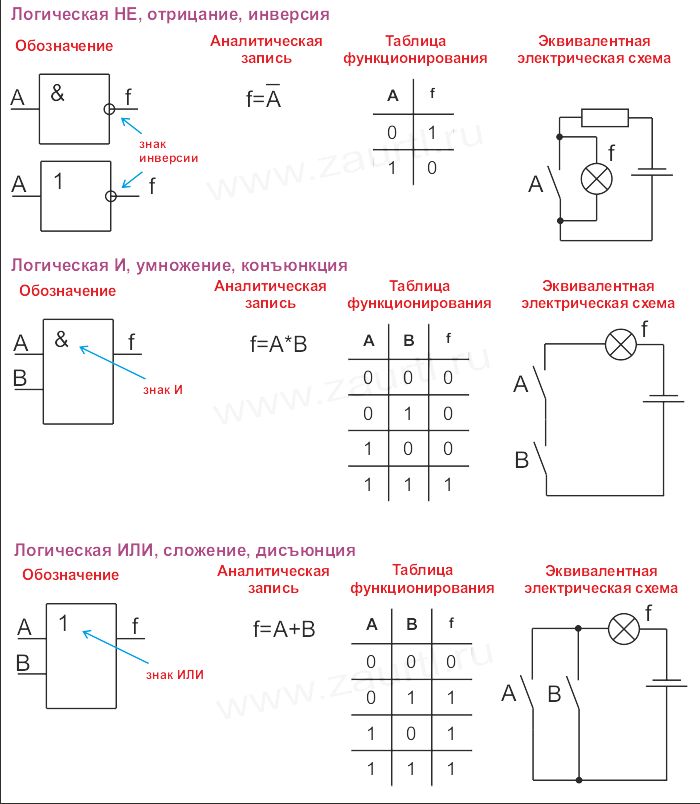
Построение таблиц истинности логических выражений.
Порядок выполнения логических операций в сложном логическом выражении.
1. Инверсия; 2. Конъюнкция; 3. Дизъюнкция; 4. Импликация; 5. Эквивалентность.
┐ & V → ≡
Для изменения указанного порядка выполнения логических операций используются скобки.
Алгоритм построения таблиц истинности для сложных выражений:
Определить последовательность выполнения логических операций (расставить порядок действий, как в математике);
Определить количество различных переменных (простых выражений);(n)
Определить количество строк (количество различных наборов 0 и 1):
количество строк = 2n ,
n - количество простых высказываний;
Подписать различные значения переменных, используя следующее правило: под первой переменной записать 2n/2 0, а затем такое же количество 1; под второй переменной (и на каждом следующем шаге) в два раза меньше 0, чем в предыдущей переменной, и в 2 раза меньше 1; последняя переменная – всегда чередование 0 и 1.
Выполнить логические операции по порядку. При этом зачёркиваем столбцы, которые уже обработали. Для каждого действия берём первые незачёркнутые значения справа и слева.
Столбец, полученный в результате выполнения последнего действия, и есть результат.
Построение логической функции по ее таблице истинности:
Попробуем решить обратную задачу. Пусть дана таблица истинности для некоторой логической функции Z(X,Y):
X |
Y |
Z |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
Составить логическую функцию для заданной таблицы истинности.
Правила построения логической функции по ее таблице истинности:
Выделить в таблице истинности те строки, в которых значение функции равно 1.
Выписать искомую формулу в виде дизъюнкции нескольких логических элементов. Число этих элементов равно числу выделенных строк.
Каждый логический элемент в этой дизъюнкции записать в виде конъюнкции аргументов функции.
Если значение какого-либо аргумента функции в соответствующей строке таблице равно 0, то этот аргумент взять с отрицанием.
Решение.
В первой и третьей строках таблицы истинности значение функции равно 1.
Так как строки две, получаем дизъюнкцию двух элементов: ( ) V ( ).
Каждый логический элемент в этой дизъюнкции запишем в виде конъюнкции аргументов функции X и Y: (X & Y) V (X & Y).
Берем аргумент с отрицанием если его значение в соответствующей строке таблицы равно 0 и получаем искомую функцию: Z (X, Y) =(¬ X & ¬Y) V (X & ¬Y).
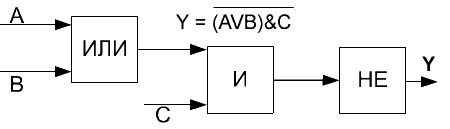
Пример 1. Логической схемы и таблицы истинности для логической функции Y=NOT((AVB)&C)
A |
B |
C |
Y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
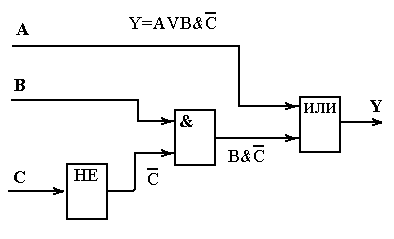
Задание №1. Построить таблицу истинности логической функции Y=AVB&(NotC)
|
|
|
Задание №2. Построить таблицу
истинности логической схемы
|
|
|
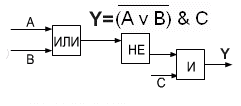
Задание №3. Построить таблицу
истинности для логической функции 
Ответ
А |
В |
С |
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
Задание №4. Построить таблицы истинности для логических функций
1)
2)
3)
Задание №5. Построить схемы выше приведенных функций в Конструкторе логических схем и проверить правильность построения таблиц истинности.
Задание № 6. Организация сравнения двух двоичных чисел заключается в выработке признака равенства (равнозначности) или признака неравенства (неравнозначности) двух сравниваемых чисел. Ограничимся признаком равенства.
Одноразрядная схема сравнения кодов
Значение признака равенства q при сравнении одноразрядных переменных описывается таблицей истинности, представленной на рисунке 3.
В ячейку в E7 введена формула: =ЕСЛИ (C7=D7; 1; 0), которая затем скопирована в ячейки D8:D10.
Значение
q1 функции виде СДНФ:
.
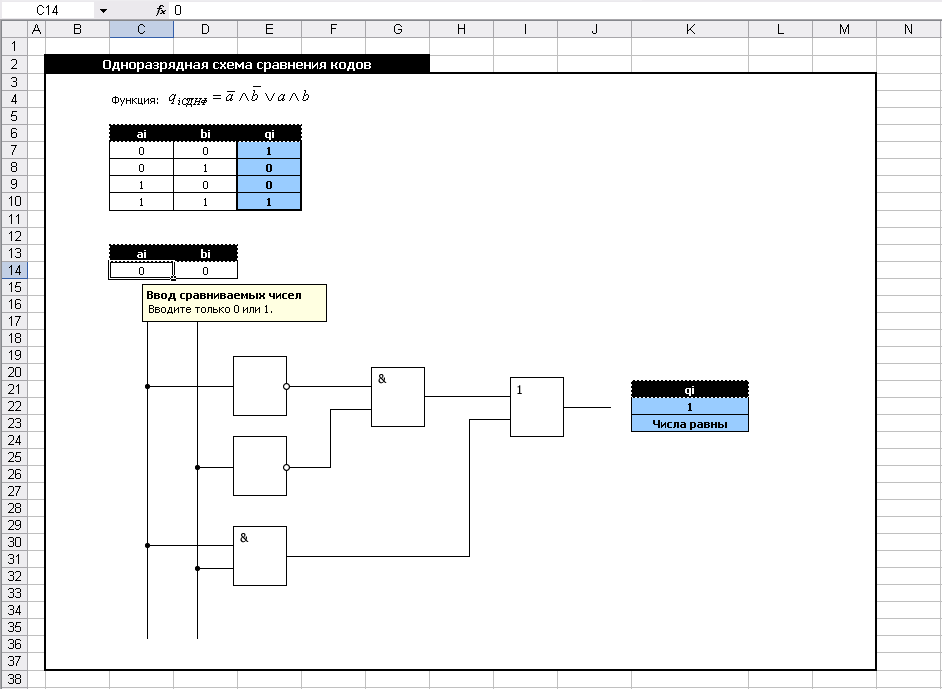
Рисунок 3 – Образец выполнения работы
Упрощение выражения не требуется, пункт 3 порядка проектирования логических схем отсутствует.
Схема имеет вид, представленный на рисунке 3. Схема начерчена непосредственно в Excel с помощью панели рисования с использованием таких приемов, как копирование повторяющихся элементов, группировка.
Дальнейшая работа проделана для того, чтобы получить действующую модель схемы, которая при подаче входных сигналов (сравниваемых одноразрядных двоичных чисел) будет выдавать выходные сигналы (результат сравнения).
Ячейки C14 и D14 отведены для ввода сравниваемых одноразрядных двоичных чисел. Им присвоены имена а и b соответственно.
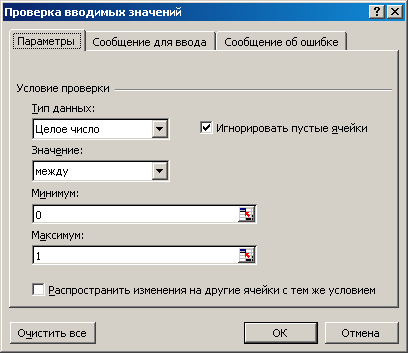
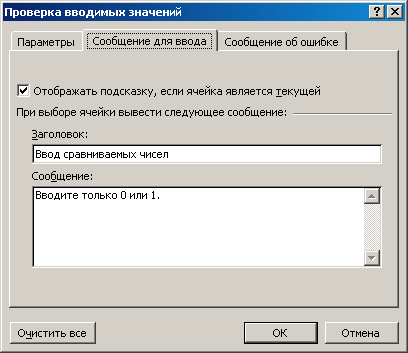
Установлена проверка данных на корректность (ввод только 0 и 1). (рисунки 4 – 5.)
Рисунок 4 – Подсказка при вводе значений
Рисунок 5 – Сообщение об ошибке, в случае ввода некорректных данных
Для этого ячейки C14 и D14 выделены и выполнена команда Данные, Проверка. В диалоговом окне Проверка вводимых значений установить нужные параметры (рисунки 6, а-в).
Рисунок 6 а – Настройка проверки вводимых значений |
Рисунок 6 б – Настройка проверки вводимых значений |
Рисунок 6 в-Настройка проверки вводимых значений
В ячейку K22 введена формула:
=ЕСЛИ (ИЛИ(И (НЕ(C14); НЕ(D14)); И (C14; D14))=ИСТИНА; 1; 0).
Функция ЕСЛИ используется лишь для преобразования значения «ИСТИНА» в 1, а значения «ЛОЖЬ» в 0.
В ячейку K23 введена формула:
=ЕСЛИ (K22=1; «Числа равны»; «Числа не равны»).
Для того чтобы случайно что-то не испортить на листе, лист защищен, кроме ячеек, в которые вводятся сравниваемые числа. Эти ячейки выделены, и выполнена команда Формат, Ячейка, на вкладке Защита снят флажок Защищаемая ячейка. Затем выполнена команда Сервис, Защита, Защитить лист.
На рисунке 3 показан вариант, когда на входы схемы аi, и bi поступают два нуля, на выходе схемы имеем q1 (числа равны). Подавая на входы другие комбинации 0 и 1, можно увидеть, что схема работает точно так, как описывает таблица истинности. Можно дополнительно ввести формулы для проверки сигналов на выходах любых элементов схемы.
Многоразрядная схема сравнения кодов
Признак равенства двухразрядных чисел q принимает значение 1, если выполняется попарно равенство всех разрядов двоичных чисел.
Для примера приведена двухразрядная схема (рисунок 7), что связано лишь с тем, что неудобно рассматривать работу схемы, если она выходит за пределы экрана. Двухразрядная схема состоит из двух одноразрядных схем.
Ячейки C7 и D7 отведены для поразрядного ввода первого числа, им присвоены имена a1 и а0 соответственно. Ячейки E7 и F7 отведены для ввода второго числа, им присвоены имена b1 и b0 соответственно.
В ячейку L7 введена формула для выдачи результата сравнения старших разрядов чисел:
=ИЛИ (И(НЕ(C7); НЕ(E7)); И (C7; E7)).
В ячейку L46 введена формула для выдачи результата сравнения младших разрядов чисел:
=ИЛИ (И(НЕ(F7); НЕ(D7)); И (F7; D7)).
В ячейку O22 введена формула для выдачи признака равенства чисел:
=ЕСЛИ (И(L46; L7)=ИСТИНА; 1; 0).
В ячейку O23 введена формула для выдачи сообщения о результате сравнения чисел:
=ЕСЛИ (O22=1; «Числа равны»; «Числа не равны»).
Рисунок 7 – Двухразрядная схема сравнения кодов
На рисунке 7 представлен результат сравнения чисел 10 и 11. На экране результат сравнения равен 0 и выдано сообщение «Числа не равны».
Домашнее задание
Построить таблицу истинности для логической функции:
С
В
А
оставить логическую функцию по функциональной схеме и определить сигнал на выходе, если А=1, В=0:
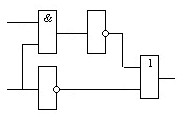
В А
Составить логическую функцию по таблице истинности и построить функциональную схему устройства:
-
X
Y
Z
F
0
0
0
0
0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
0