
- •Практическое занятие №1 Тема: Кодирование информации. Системы счисления. Представление чисел в разных системах счисления.
- •Задания для практического занятия и инструктаж по их выполнению
- •Теоретические сведения
- •Задания.
- •Домашнее задание.
- •Практическое занятие №2. Тема: Правила недесятичной арифметики. Сложение, умножение, деление, сдвиг.
- •Задания для практического занятия и инструктаж по их выполнению
- •Теоретические сведения
- •Дополнительные задания:
- •Задания для самостоятельного решения (домашнее задание)
- •Практическое занятие №3 Тема: Логические операции в эвм. Основные логические функции
- •Теоретические сведения
- •Построение таблиц истинности логических выражений.
- •Практическое занятие №4. Тема: Логические элементы шифраторы и дешифраторы.
- •Теоретические сведения
- •Практическое занятие №5 Тема: Логические элементы мультиплексоры, пороговые ячейки.
- •Теоретические сведения
- •Практическое занятие №6 Тема: Логические элементы триггеры. Rs-триггеры, d-триггеры, jk-триггеры.
- •Теоретические сведения
- •Практическое занятие №7. Тема: Логические элементы полусумматоры и сумматоры.
- •Задания для практического занятия и инструктаж по их выполнению
- •Теоретические сведения
- •Практическое занятие №8. Тема: Логические элементы счетчики. Прямой и обратный счетчик. Регистры
- •Теоретические сведения
- •Двоичный счетчик.
- •Практическое занятие №9. Тема: Моделирование работы узлов компьютера с помощью Excel.
- •Задания для практического занятия и инструктаж по их выполнению
- •Схемы сравнения кодов
- •Одноразрядная схема сравнения кодов
- •Многоразрядная схема сравнения кодов
- •Дешифраторы
- •Практическое занятие №10. Тема: Моделирование работы узлов компьютера с помощью Excel
- •Задания для практического занятия и инструктаж по их выполнению Сумматоры
- •Полусумматор
- •Одноразрядный сумматор
- •Многоразрядный сумматор
- •Практическое занятие №11. Тема: Установка процессора в сокет.
- •Задания для практического занятия и инструктаж по их выполнению
- •Выполнить практические задания по данной теме и оформить отчет по образцу: Теоретические сведения
- •Цель работы.
- •Задание.
- •Практическое занятие №12. Тема: Диагностика и настройка производительности процессора. Работа с утилитами.
- •Задания для практического занятия и инструктаж по их выполнению
- •Выполнить практические задания по данной теме.
- •Практическое занятие №13. Тема: Тестирование основных параметров системы. Работа с утилитами
- •Теоретические сведения
- •Практическое занятие №14. Тема: Сборка основных компонентов системы. Установка драйверов устройств.
- •Задания для практического занятия и инструктаж по их выполнению
- •Записать теоретические сведения в тетрадь.
- •Выполнить практические задания по данной теме. Теоретические сведения
- •Практическое занятие №15. Тема: Установка модулей памяти.
- •Задания для практического занятия и инструктаж по их выполнению
- •Записать теоретические сведения в тетрадь.
- •Выполнить практические задания по данной теме. Теоретические сведения
- •Практическое занятие №16. Тема: Тестирование памяти и настройка параметров bios.
- •Задания для практического занятия и инструктаж по их выполнению
- •Записать теоретические сведения в тетрадь.
- •Выполнить практические задания по данной теме. Теоретические сведения
Задания для практического занятия и инструктаж по их выполнению
Разобрать материал электронного учебника Системы счисления по данной теме.
Записать теоретические сведения в тетрадь.
Прочитать материал презентации по данной теме.
Разобрать и проанализировать примеры.
Выполнить письменно практические задания по данной теме в рабочей тетради.
Теоретические сведения
Язык чисел, как и обычный язык, имеет свой алфавит. В том языке чисел, которым сейчас пользуются практически на всем земном шаре, алфавитом служат десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Система счисления – способ представления числа символами некоторого алфавита, которые называют цифрами.
Все системы исчисления разделяют на два вида:
позиционные;
непозиционные.
Непозиционные системы счисления - это система счисления, в которой величина (значение) числа определяется как сумма или разность цифр в числе.
Позиционные системы счисления - это система счисления, в которой величина, обозначаемая цифрой, зависит от места (позиции) цифры в числе.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. |
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2+ ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m,
где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.
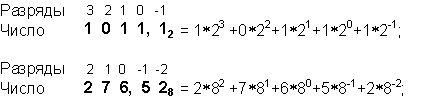
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
Сводная таблица переводов целых чисел из одной системы счисления в другую
П ример.
Число
ример.
Число
![]() перевести
в десятичную систему счисления.
перевести
в десятичную систему счисления.
![]()
Пример. Число
![]() перевести
в десятичную систему счисления.
перевести
в десятичную систему счисления.
![]()
Пример . Число
![]() перевести
в десятичную систему счисления.
перевести
в десятичную систему счисления.
![]()
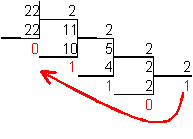
Пример. Число
![]() перевести
в двоичную систему счисления.
перевести
в двоичную систему счисления.
![]()
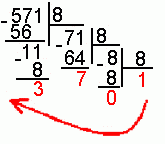
Пример. Число
![]() перевести
в восьмеричную систему счисления.
перевести
в восьмеричную систему счисления.
![]()
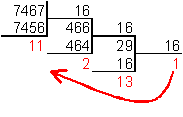
Пример. Число
![]() перевести
в шестнадцатеричную систему счисления.
перевести
в шестнадцатеричную систему счисления.
![]()
Пример. Число
![]() перевести
в восьмеричную систему счисления.
перевести
в восьмеричную систему счисления.
![]()
Пример. Число
![]() перевести
в шестнадцатеричную систему счисления.
перевести
в шестнадцатеричную систему счисления.
![]()
Пример. Число
![]() перевести
в двоичную систему счисления.
перевести
в двоичную систему счисления.
![]()
Пример. Число
![]() перевести
в двоичную систему счисления.
перевести
в двоичную систему счисления.
![]()
Пример 1. Число
![]() перевести
в восьмеричную систему счисления.
перевести
в восьмеричную систему счисления.
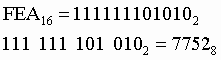
Пример. Число
![]() перевести
в шестнадцатеричную систему счисления.
перевести
в шестнадцатеричную систему счисления.

Задания.
1. Переведите целые числа из десятичной системы счисления в двоичную:
а)513; в)600; д)602; ж)1000;
б)2304; г)5001; е)7000; з)8192.
2. Переведите десятичные дроби в двоичную систему счисления (ответ записать с шестью двоичными знаками):
а)0,4622; в)0,5198; д)0,5803; ж)0,6124;
б)0,7351; г)0,7982; е)0,8544; з)0,9321.
3. Переведите смешанные десятичные числа в двоичную систему счисления:
а)40,5; б)31,75; в)124,25; г)125,125.
4. Переведите целые числа из десятичной в восьмеричную систему счисления:
а) 8700; б)8888; в)8900; г)9300.
5. Переведите целые числа из десятичной в шестнадцатеричную систему счисления:
а)266; б)1023; в)1280; г)2041.
6. Переведите числа из десятичной системы счисления в восьмеричную:
а) 0,43; б) 37,41; в) 2936; г)481,625.
7. Переведите числа из десятичной системы счисления в шестнадцатеричную:
а) 0,17; б)43,78; в)25,25; г)18,5.
8. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основанием 2, 8, 10 и 16.
Основание 2 |
Основание 8 |
Основание 10 |
Основание 16 |
101010 |
|
|
|
|
127 |
|
|
|
|
321 |
|
|
|
|
2А |
9. Переведите двоичные числа в восьмеричную систему счисления:
а)1010001001011; в)1011001101111; д)110001000100;
б)1010,00100101; г)1110,01010001; е)1000,1111001.
10. Переведите двоичные числа в шестнадцатеричную систему счисления:
а)1010001001011; в)1011001101111; д)110001000100;
б)1010,00100101; г)1110,01010001; е)100,1111001.
11. Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления:
а)2668; в)12708; д)10,238;
б)26616; г)2а1916; е)10,2316.
12. 13. Перевести числа из восьмеричной системы счисления в шестнадцатеричную:
-
а) 12754;
б) 1515;
в) 7403.
14. Перевести числа из шестнадцатеричной системы счисления в восьмеричную:
-
а) 1АЕ2;
б) 1С1С;
в) 34Е.
