Задания для практического занятия и инструктаж по их выполнению Сумматоры

Сумматором называется узел арифметического устройства, реализующий ал­гебраическое суммирование чисел, представленных сигналами на его входах.

Числа в любой позиционной системе счисления складываются поразрядно, по­этому сложить любые двоичные числа можно при наличии узлов, реализующих суммирование цифр одного разряда с учетом возможного переноса из соседнего млад­шего разряда. К таким узлам относятся одноразрядные сумматоры на 2 и 3 входа.

Полусумматор

Полусумматор — это логический узел, предназначенный для суммирования двух одноразрядных двоичных чисел. Он имеет 2 входа — а_i и b_i и 2 выхода — р_i+1 и s_i.

р_i+1 — выход переноса в следующий разряд;

s_i — выход суммы.

Полусумматор используется для сложения младших разрядов чисел, где отсут­ствует перенос из предыдущего разряда.

1. Логика работы полусумматора описывается таблицей истинности, представ­ленной на рис. 10 (1).

2. На рис. 10(2) представлены выражения для р_i+1 и s_i в СДНФ.

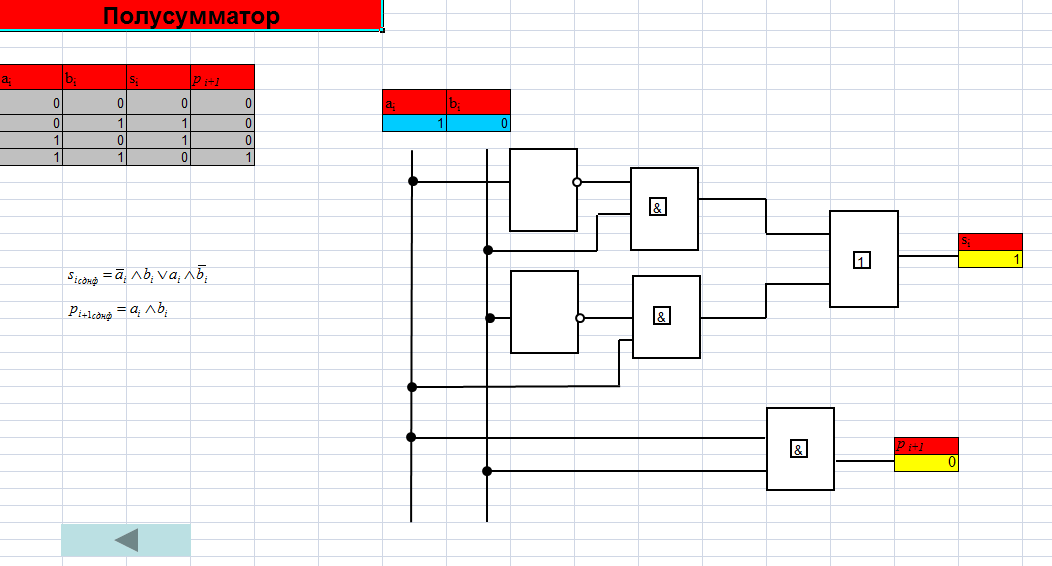
Рис. 10

3. Упрощение выражения не требуется, пункт 3 порядка проектирования логи­ческих схем отсутствует.

4. Схема имеет вид, представленный на рис. 10. Ячейки Н8 и 18 отведены для ввода суммируемых чисел. Им присвоены имена а и b соответственно.

Установлена проверка данных на корректность (ввод только 0 и 1).

Ячейка Р17 отведена для выхода s_i , в нее введена формула

=ЕСЛИ(ИЛИ(И(НЕ(а);b);И(НЕ(b);а))=ИСТИНА;1;0).

Ячейка Р29 отведена для выхода р_i+1, в нее введена формула

=ЕСЛИ(И(а;b)=ИСТИНА; 1 ;0).

Лист защищен за исключением ячеек, в которые вводятся слагаемые.

На рис. 10 показан вариант, когда на входы схемы а_i и b_i поступают две едини­цы. При этом на выходе s_i получаем 0, а на выходе р_i+1 — 1 соответственно.

Подавая на входы другие комбинации 0 и 1, можно увидеть, что схема дей­ствительно выполняет алгебраическое сложение одноразрядных двоичных чисел. Можно дополнительно ввести формулы для проверки сигналов на выходах любых элементов схемы.

Для большей наглядности на рабочем листе снята сетка.

Одноразрядный сумматор

Одноразрядный комбинационный сумматор — это логический узел, предназна­ченный для суммирования трех одноразрядных двоичных чисел. Он имеет три входа — а_i, b_i и р_i и два выхода — р_i+1 и s_i.

На входы a_i, b_i поступают значения суммируемых цифр данного разряда, а на вход р_i — значение переноса из соседнего младшего разряда.

1. Логика работы одноразрядного сумматора описывается таблицей истиннос­ти, представленной на рис. 11 (1).

Puc. 11

2. На рис. 11 (2) представлены выражения для р_i+1 и s_i в виде СДНФ.

3. На рис. 11 (3) представлено упрощение выражения для р_i+1 с помощью карт Карно. Упрощение выражения для s_i на листе не приводится из-за громоздкости. Оно выполнено с использованием законов алгебры логики. Упрощенное выраже­ние для s_i представлено через р_i+1.

4. Схема имеет вид, представленный на рис. 12 (4). Она построена на отдель­ном листе.

Ячейки В7 и С7 и D7 отведены для ввода суммируемых чисел. Им присвоены имена а, b и р соответственно.

Установлена проверка данных, вводимых в ячейки с именами а, b и р на кор­ректность (ввод только 0 и 1).

Ячейка Р11 отведена для выхода р_i+1, ей присвоено имя pi1, и в нее введена формула

=ЕСЛИ(ИЛИ(И(а;b);И(a;p);И(b;р))=ИСТИНА;1;0).

Ячейка Р32 отведена для выхода s_i, в нее введена формула

=ЕСЛИ(ИЛИ(И(а;b;р);И(НЕ(рi1);ИЛИ(а;b;р)))=ИСТИНА;1;0.

Лист защищен за исключением ячеек, в которые вводятся слагаемые.

На рис. 12 показан вариант, когда на входы схемы a_i, b_i и р_i поступают три единицы. При этом на выходе s_i получаем 1 и на выходе р_i+1 - 1.

Рис. 12

Подавая на входы другие комбинации 0 и 1, можно увидеть, что схема дей­ствительно выполняет алгебраическое сложение одноразрядных двоичных чисел. Можно дополнительно ввести формулы для проверки сигналов на выходах любых элементов схемы.