2.2. Объект регулирования

Объектом регулирования называют аппарат, механизм или систему, в которых посредством авторегулятора поддерживается заданное значение параметра регулирования. Математическая модель или характеристика объекта регулирования представляет собой математическую зависимость между входными и выходными величинами объекта. В химической промышленности объекты весьма разнообразны. Объектом может быть вещество, аппарат или часть аппарата (куб ректификационной колонны). Объект может быть из нескольких аппаратов, соединенных между собой.

Объекты, в которых регулируемые величины в равновесном состоянии имеют одинаковое значение по всему объему объекта, называются объектами с сосредоточенными параметрами. Объекты, в которых значения регулируемых величин в различных точках объекта неодинаковы, как в равновесном, так и в переходном режиме, называются объектами с распределенными параметрами. Эти объекты описываются дифференциальными уравнениями в частных производных. Пример, трубопровод с транспортируемым по нему газом (давление газа по течению неодинаково из-за потери на трение и местного сопротивления).

Основные свойства объектов: емкость, нагрузка, самовыравнивание, запаздывание

1. Емкостью объекта называют то количество вещества или энергии, которое содержится в объекте в данный момент. Часто и само устройство, в котором происходит накопление энергии, называют емкостью. По количеству емкостей объекты подразделяются на одноемкостные и многоемкостные.

2. Нагрузка – количество энергии или вещества, отбираемое из объекта регулирования для каких-либо целей в установившемся режиме.

3. Самовыравнивание – способность объекта самостоятельно восстанавливать нарушенное равновесие между подачей и потреблением вещества за счет отклонения регулируемого параметра.

Одноемкостный объект с самовыравниванием

Статическая характеристика объекта с самовыравниванием - это эависимость Х_вых = f (Х_вх) в установившемся режиме (рис. 2.3). За входную величину Х_вх принимаем поступление вещества в емкость в л/мин (рис.2.3) (например, 3 л/мин), за выходную Х_вых – уровень в емкости в метрах. В установившемся режиме количество поступающего вещества равно выходящему 3 л/мин (т.е. нагрузке), в результате уровень не меняется (например, 1 м). Когда приток увеличивается скачком, например, до 30 л/мин, уровень начинает расти. С ростом уровня возрастает гидростатическое давление на дно сосуда. В результате увеличивается скорость истечения жидкости из емкости – V. Так как площадь выходного отверстия F в емкости не меняется, то расход на выходе также возрастает (Q=F*V). Затем, за счет увеличения гидростатического давления на дно сосуда, наступит равновесие (установившийся режим), т.е. нагрузка = 30л/мин. Уровень установился на новой отметке (например, 2,5 м). В этот момент можно измерять новый установившийся уровень и результат наносить на график статической характеристики. Далее приток вновь увеличиваем скачком. В установившемся режиме получим для статической характеристики также третью точку и т.д.

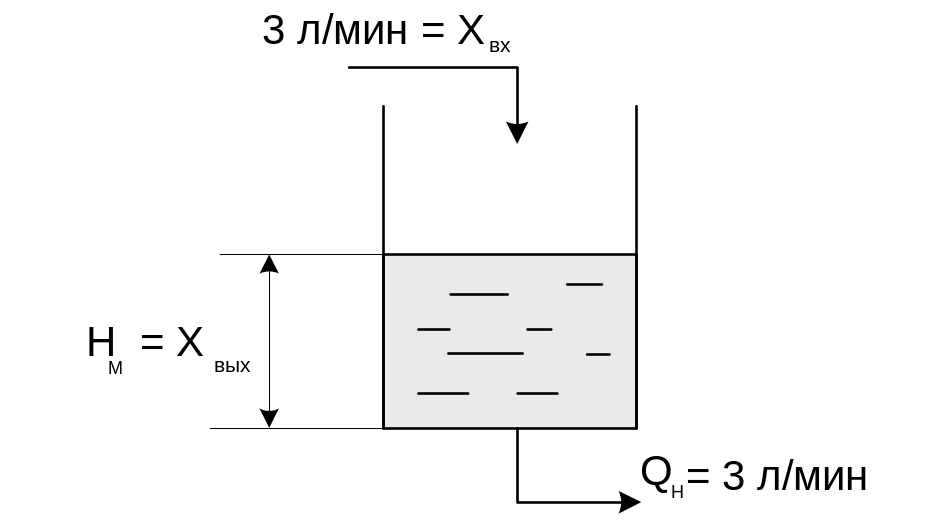
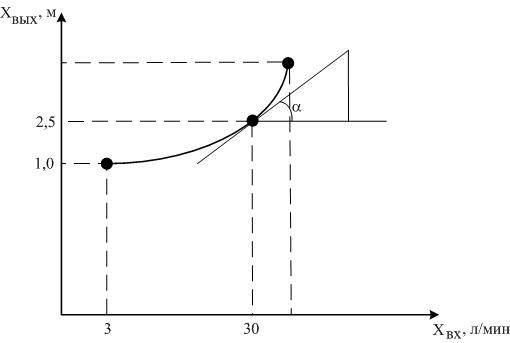
Рис. 2.20. Статическая характеристика объекта c самовыравниванием.

Статическая характеристика строится для определения коэффициента усиления К. Если статическая характеристика нелинейная, как здесь, то ее иногда линеаризуют. Если статическая характеристика линейная, то коэффициент усиления для нее только один – общий.

Так как в данном случае характеристика нелинейная, то понятие коэффициента усиления можно отнести только к какой-то точке кривой. Выбирается точка, проводим в ней касательную.

Динамическая характеристика одноемкостного объекта с самовыравниванием - это эависимость Х_вых = f (Х_вх) в неустановившемся режиме. Здесь  – время (рис.2.4). После нанесения возмущения на входе скачком с 3л/мин до 30л/мин, каждую секунду измеряем возрастающий уровень до установления нового уровня. Получим график кривой. (рис. 2.4).

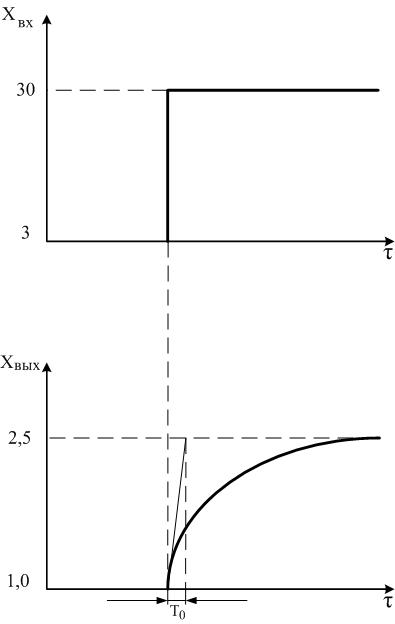
Рис.2.21. Динамическая характеристика объекта c самовыравниванием.

К полученной кривой проводим касательную в точке Х_вых = 1 м до пересечения с новым установившимся уровнем Х_вых = 2,5м, затем опускаем перпендикуляр. Полученный отрезок на оси времени Т_о – постоянная времени объекта. Ради определения Т_о и была построена динамическая характеристика объекта.

Объект с самовыравниванием по типу динамической характеристики эквивалентен апериодическому звену I порядка и описывается обыкновенным дифференциальным уравнением I–го порядка с постоянными коэффициентами (экспонента).

Найденные из статической и динамической характеристик константы K и Т_о подставляем в дифференциальное уравнение и, решив его, получим

.*

Таким образом, можно построить аналитическую динамическую характеристику в координатах (Х_вых, τ). Кроме того, найденное решение можно использовать в программах ПК (не нужно вводить в ПК таблицы экспериментальных результатов, а вместо них вводим формулу*). Этот процесс называется «математическая идентификация объекта».

Влияние емкости объекта на величину постоянной времени

Рассмотрим влияние емкости объекта на величину постоянной времени Т_о. Установим обогреватели одинаковой мощности в двух помещениях имеющих разный объем. Считаем, что температуры в этих помещениях вначале были одинаковы. Так как объем первого из помещений меньше объема второго, то в первом случае температура установится быстрее, чем во втором. Кроме того, установившаяся температура в помещении меньшего объема будет выше, чем в помещении большего объема при одной и той же мощности обогревателей. При построении динамических характеристик этих помещений получим Т_о первого помещения меньше Т_о комнаты имеющей больший объем (рис.2.5). Следовательно, чем меньше емкость объекта, тем меньше постоянная времени Т_о.

Рис. 2.22. Динамические характеристики объектов c самовыравниванием.

Одноемкостный объект без самовыравнивания.

Динамическая характеристика

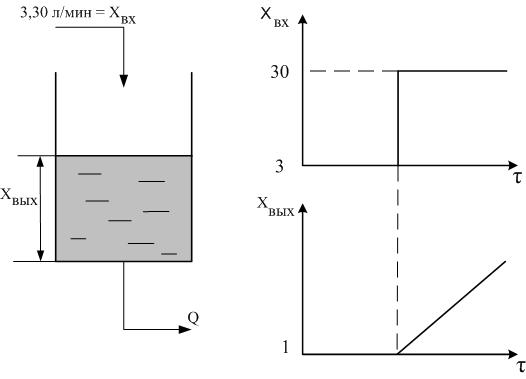
Рис.2.23. Динамическая характеристика объекта без самовыравнивания.

Одноемкостный объект без самовыравнивания эквивалентен интегрирующему звену (рис.2.6.). При увеличении притока на входе скачком, например, до 30 л/мин, уровень неограниченно растет, самовыравнивания не наступает, т.к. выходное отверстие емкости засорилось (либо там установлен насос постоянной производительности).

Многоемкостный объект с самовыравниванием

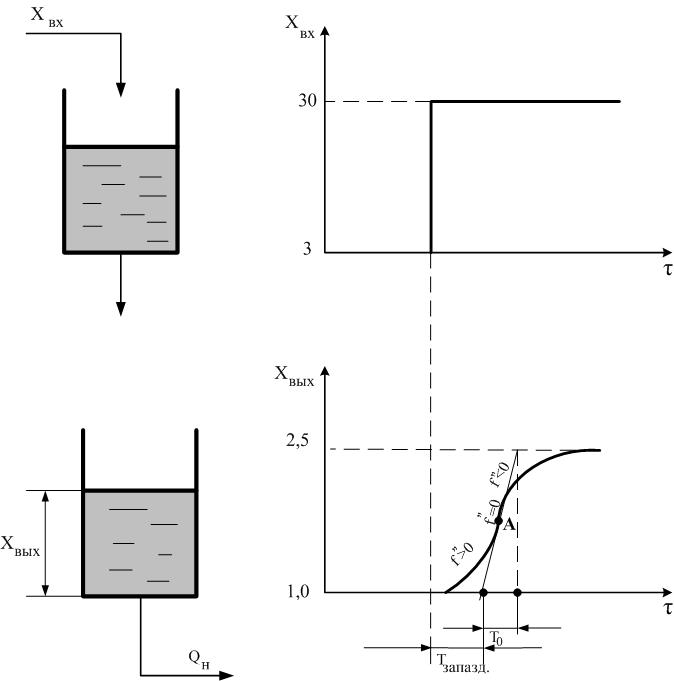
Рис. 2.24. Динамическая характеристика многоемкостного

объекта с самовыравниванием.

Многоемкостный объект (в нашем случае двухемкостный) с самовыравниванием по типу динамической характеристики эквивалентен апериодическому звену II порядка и описывается обыкновенным дифференциальным уравнением II – го порядка с постоянными коэффициентами (две экспоненты).

Динамическая характеристика (рис.2.7.) описывается дифференциальным уравнением II порядка. Входная величина X_вх, выходная величина X_вых, т.е. уровень во 2-й емкости.

После нанесения скачка X_вх с 3 л/мин до 30 л/мин уровень во 2-й емкости увеличивается вначале с возрастающей скоростью (здесь f^" > 0), а затем с убывающей скоростью (f^" < 0). Точка А – это точка перегиба (f^" = 0). В итоге, после нанесения скачка X_вх с 3 л/мин до 30 л/мин уровень во 2-й емкости установиться на отметке, например, 2,5 м. Здесь Т_зап – время запаздывания; Т_о – постоянная времени. Чем больше расстояние между емкостями, тем выше смещается точка перегиба А (т.е. увеличивается время запаздывания).

Многоемкостный объект без самовыравнивания

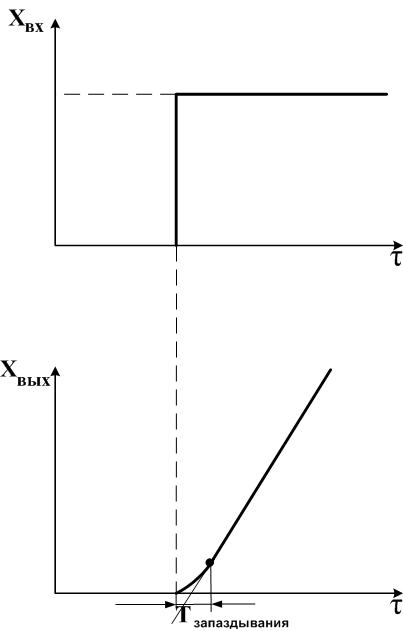
Рис.2.25. Динамическая характеристика многоемкостного (двухемкостного)

объекта без самовыравнивания.

Многоемкостный объект без самовыравнивания по типу динамической характеристики (рис.2.8.) эквивалентен интегрирующему звену. При увеличении притока на входе скачком, например, до 30 л/мин, уровень растет, но самовыравнивания во 2-й емкости не наступает, т.к. выходное отверстие этой емкости засорилось (либо там установлен насос постоянной производительности).

Запаздывание в объектах и регуляторах

В реальных объектах (регуляторах) изменение регулируемого параметра начинается не сразу после нанесения возмущения, а спустя некоторое время. Это время называют запаздыванием. Различают 2 вида запаздывания: чистое (транспортное) – τ₀; емкостное - τ_е. Соответственно – полное запаздывание.

В одноемкостном объекте имеется только чистое запаздывание τ₀. Оно вызывается наличием в регулируемом объекте участков, по которым распространение сигнала требует некоторого времени.

В многоемкостном, (двух и более объектов), кроме чистого имеется еще и емкостное запаздывание τ_е. Емкостное запаздывание обусловлено гидравлическими тепловыми и другими сопротивлениями. Эти сопротивления вызывают замедленный переход вещества из одной емкости в другую.

Рассмотрим динамическую характеристику одноемкостного объекта с самовыравниванием с учетом запаздывания (рис. 2.9).

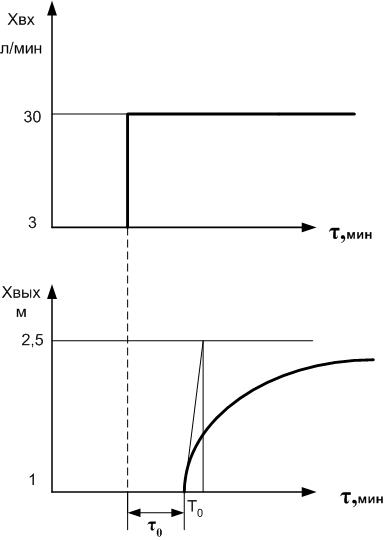
Рис. 2.26. Динамическая характеристика одноемкостного объекта

с самовыравниванием с учетом запаздывания.

Как следует из рис.2.9 кривая разгона смещается вправо на время чистого (транспортного) запаздывания τ_0.

2.3. Автоматический регулятор

Автоматический регулятор – это совокупность устройств, при помощи которых автоматически поддерживается значение регулируемой величины с той или иной точностью по отношению к заданному значению. По роду используемой энергии регуляторы подразделяют на:

1. пневматические;

2. гидравлические;

3. электрические;

4. электрогидравлические.

Зависимость μ = f (σ) в неустановившемся режиме называется законом регулирования регулятора, где σ = (Т_тек – Т_зад) – сигнал рассогласования, μ – закон перемещения затвора регулирующего органа,  – время. Здесь:

Т_тек – текущее значение регулируемого параметра;

Т_зад– заданное значение регулируемого параметра.

Динамическая характеристика регулятора как динамического звена рассматривается всегда в следующих координатах:

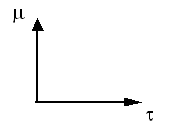
В зависимости от закона регулирования регулятора бывают линейные и нелинейные.

В настоящее время роль регуляторов выполняют программируемые контроллеры. В них запрограммирован закон регулирования (чаще всего – ПИД закон).

Классификация линейных регуляторов

1. П-регулятор (пропорциональный);

2. И-регулятор (интегральный);

3. ПИ-регулятор (пропорционально-интегральный (изодромный));

4. Регуляторы с предварением (с опережением):

   • ПД-регулятор (пропорционально-дифференциальный);

   • ПИД-регулятор (пропорционально-интегрально-дифференциальный).

Из нелинейных регуляторов наиболее популярен позиционный регулятор.

Рассмотрим смысл закона регулирования регулятора на примере САР температуры целевого продукта в теплообменнике. Эта схема нам уже известна. Это САР по отклонению. Здесь σ – сигнал рассогласования 90º – 100º = –10 ºС  σ. Закон регулирования регулятора (контроллера) определяет характер перемещения затвора регулирующего органа в новое положение.

На место регулятора (контроллера) в данной схеме будем поочередно ставить линейные регуляторы и, будем наблюдать, как регулирующее воздействие μ от каждого закона регулирования влияет на характер перемещения затвора регулирующего органа.

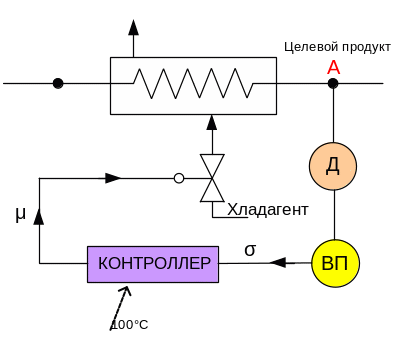
П-регулятор

Это регулятор, у которого μ пропорционально σ, т.е.

μ = – Кσ.

При скачке входной величины σ на значение (–10ºС) затвор регулирующего органа переходит в новое μ - положение скачком (рис.2.12). Поэтому П-регуляторы применяются там, где нет строгого требования к точности регулирования.

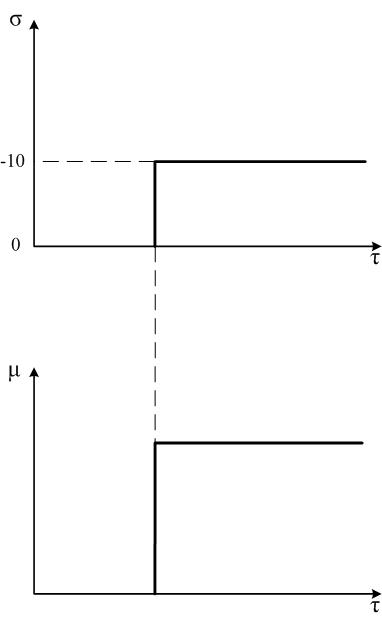
Рис.2.27. Закон регулирования П-регулятора.

Достоинство такого регулирования: регулирующий орган быстро перемещается на новое положение, т.е. высокая скорость регулирования.

Недостаток: имеет место остаточное отклонение, т.е. имеет место некоторая ошибка регулирования.

И-регулятор

Это регулятор, у которого μ пропорционально интегралу σ

При скачке входной величины на значение (–10ºС) затвор регулирующего органа медленно переходит в новое положение (рис.2.13).

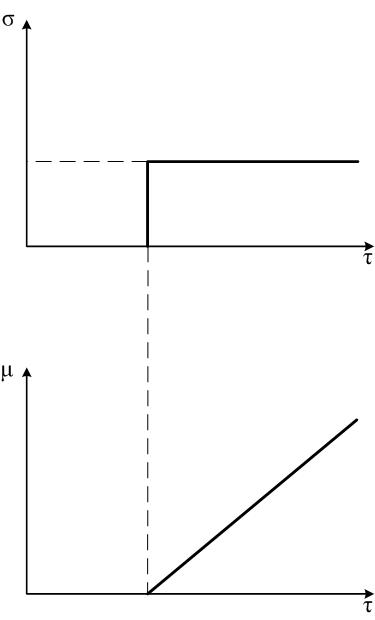
Рис.2.28. Закон регулирования И-регулятора.

Как бы ни было мало отклонение регулируемой величины от заданного значения, интегральный регулятор будет продолжать перемещать регулирующий орган вплоть до необходимого положения.

Достоинство: отсутствие остаточного отклонения регулируемого параметра от заданного значения.

Недостаток: низкая скорость регулирования, т.е. затвор в новое положение перемещается медленно.

ПИ-регулятор

Это параллельное соединение предыдущих двух регуляторов (П и И - регуляторов). Этот регулятор сочетает положительные моменты П и И -регуляторов.

У ПИ-регулятора (рис.2.14) регулирующее воздействие μ перемещает затвор пропорционально отклонению параметра σ и интегралу отклонения σ.

,

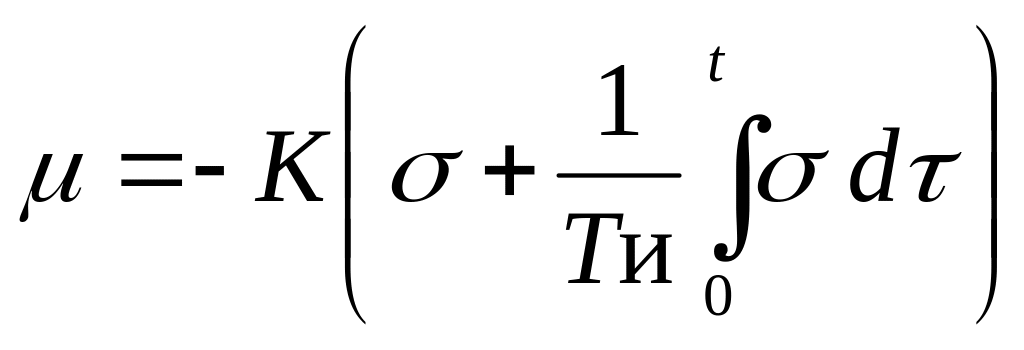где: К, Т_и – параметры настройки регулятора. Как видим, математическое выражение данного закона – это сумма двух предыдущих формул. Затвор регулирующего органа часть пути (а, б) пройдет скачком по П-закону, а оставшуюся часть (б, в) – медленно по И - закону.

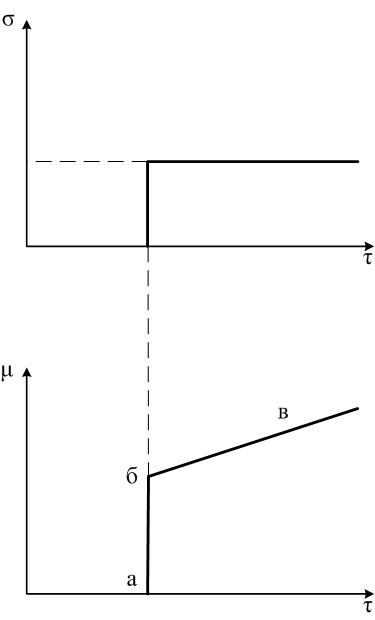
Рис.2.29. Закон регулирования ПИ-регулятора.

Регуляторы с предварением

ПД-регулятор

Это такой регулятор (рис.2.15), у которого выходной сигнал μ пропорционален входному сигналу σ и производной dσ/d, т.е.

.

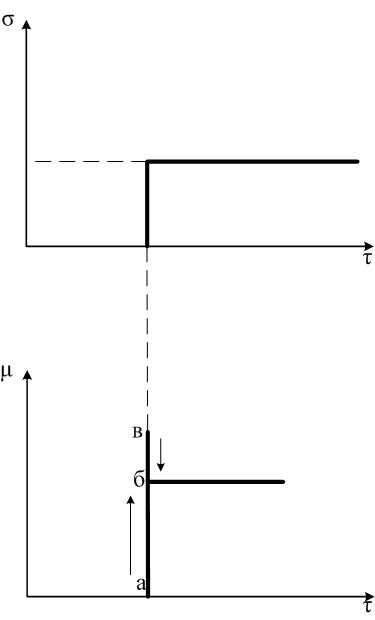
Рис.2.30. Закон регулирования ПД-регулятора.

Производная dσ/d характеризует тенденцию изменения (отклонения) регулируемой величины. Величина и знак воздействия от производной позволяют регулятору как бы предвидеть в какую сторону и на сколько отклонилась бы регулируемая величина под действием данного возмущения. Это предвидение позволяет регулятору предварять своим воздействием возможное отклонение регулируемой величины. В результате процесс регулирования завершается в более короткое время. Сначала затвор скачком переходит из точки а в точку в (П – закон), т.е. больше чем надо, затем отскакивает назад в точку б (дифференциальное действие) и остается в этом положении.

ПИД-регулятор

У него 3 родителя: П-регулятор, И-регулятор, ПД-регулятор. Соответственно складываются 3 формулы (рис.2.16.)

.

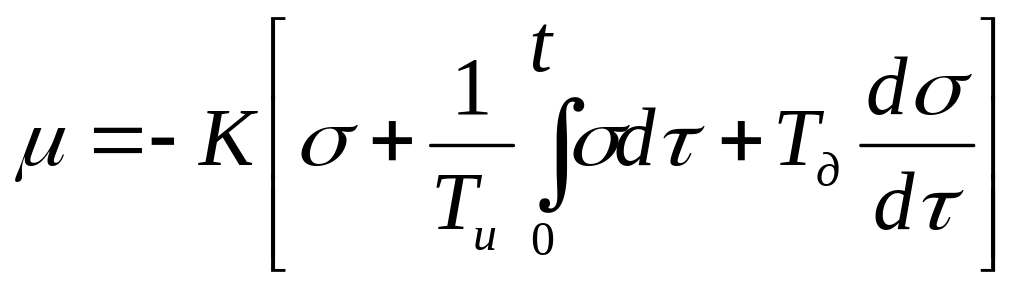Здесь: К, Т_и, Т_д – параметры настройки, которые можно настроить вручную.

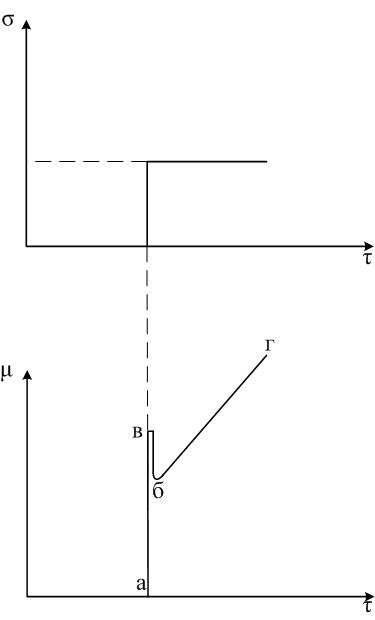
Рис.2.31. Закон регулирования ПИД-регулятора.

ПИД - закон используется во многих контроллерах. Сначала затвор скачком переходит из точки а в точку в (П – закон), т.е. больше чем надо, затем отскакивает назад в точку б (дифференциальное действие), а далее затвор медленно перемещается в конечное положение г (И – закон). В результате процесс регулирования завершается в более короткое время и с меньшей погрешностью регулирования.

Итак, рассмотрены идеальные характеристики линейных регуляторов. В реальности все происходит во времени (см. рис.2.18а – ПИД-закон регулирования идеальный, 2.18б – ПИД-закон регулирования реальный).

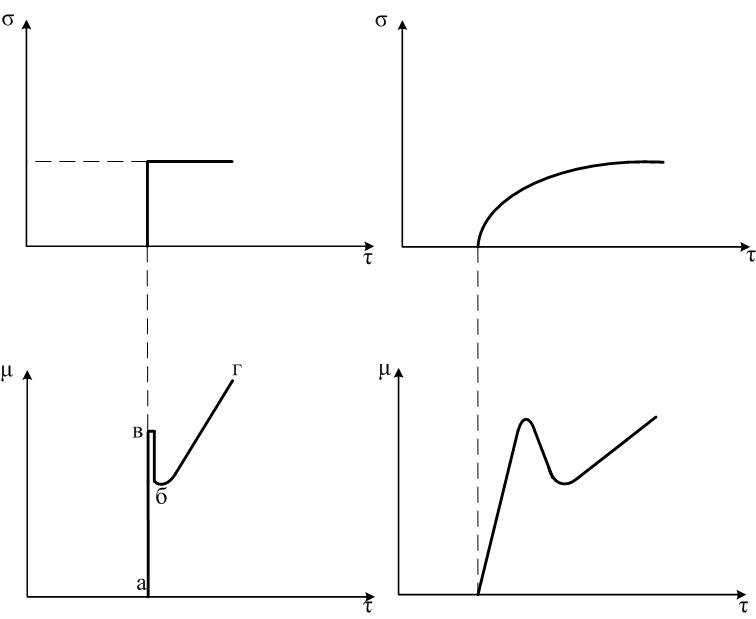
(а) (б)

Рис.2.32. ПИД – закон идеальный (а) и реальный (б)

с учетом действия по времени.

Кроме того, в графиках нужно учитывать запаздывание (чистое (транспортное) – τ₀

и емкостное запаздывание- τ_е).

Нелинейные регуляторы

Позиционный регулятор

У позиционных регуляторов регулирующее воздействие заставляет затвор срабатывать только при определенных отклонениях регулируемого параметра от заданной величины. Регулирующий орган позиционного регулятора может занимать ограниченное число определенных позиций. Перемещение из одного положения в другое происходит мгновенно. Примером может быть контактная пара (регулирующий орган) для включения ТЭНа в сауне. Регулирующий орган - контактная пара имеет только 2 позиции (вкл., выкл.). Наиболее распространены двухпозиционные регуляторы. При использовании двухпозиционной САР регулируемый параметр совершает незатухающие синусоидальные колебания (рис.2.17.).

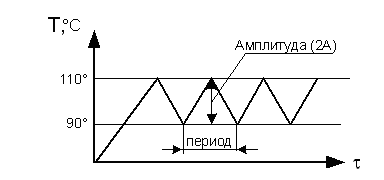
Рис.2.33. Закон регулирования двухпозиционного регулятора.