2.1.2. Передаточные функции типовых динамических звеньев.

1. Усилительное звено

,

где к – коэффициент усиления звена (0<k<); .

2. Апериодическое звено 1-го порядка

,

где – постоянная времени звена, зависящая от конструкции и принципа действия звена.

,

т.е.

3. Интегрирующее звено (астатическое)

,

,

.

4. Колебательное звено

,

где Т₁, Т₂, к – постоянные коэффициенты.

получим ,

,

т.е. .

5. Апериодическое звено 2-го порядка

,

где Т₁, Т₂, к – постоянные коэффициенты.

Получим ,

, т.е. .

6. Дифференцирующее звено

;

, т.е. .

Структурные схемы систем соединения звеньев

Схемы САР, представленные соединениями элементарных динамических звеньев, называются структурными. Составление структурных схем облегчает анализ и синтез реальных систем. Для динамических характеристик САР имеет значение порядок соединения звеньев между собой.

Рассмотрим следующие виды соединений звеньев:

1. Последовательное;

2. Параллельное;

3. Соединение звеньев по принципу обратной связи (параллельно-встречное).

Последовательное соединение звеньев

При таком соединении х_вых предыдущего звена является входной величиной – х_вх для последующего звена.

Дана система из трех последовательно соединенных звеньев (рис. 2.17).

Рис. 2.17. Последовательное соединение звеньев

Найдем W(p) для всей системы звеньев.

Решение:

Так как для каждого звена , то

;

;

.

Но , .

Таким образом, после подстановки получим .

Тогда, рассматривая систему соединений трех звеньев, как единое звено, получим .

Таким образом, при последовательном соединении n звеньев передаточная функция всей системы равна:

.

Пример: Дана система из трех последовательно соединенных звеньев: усилительное звено и два апериодических звена первого порядка. Их передаточные функции следующие: ; ; .

Найти передаточную функцию системы.

Решение:

В соответствии с полученным ранее выражением имеем:

.

Таким образом, данная система из трех последовательно соединенных динамических звеньев представляет собой апериодическое динамическое звено второго порядка, а именно:

.

Здесь, Т₁+Т₂=11; Т₁Т₂=28, т.е. Т₁=4, Т₂=7, .

Параллельное соединение звеньев

При данном соединении звеньев один и тот же входной сигнал подается на вход двух и большего числа звеньев. При этом значения выходных величин суммируются.

Рис. 2.18. Параллельное соединение звеньев

Здесь ;

.

,

Но ; ; .

В результате получим: .

Соответственно для «n» параллельно соединенных звеньев получим звено с передаточной функцией:

.

Соединение звеньев по принципу обратной связи

(параллельно-встречное)

Рассмотрим структурную схему (рис. 2.19).

Рис. 2.19. Параллельно-встречное соединение звеньев

При таком соединении звеньев подается на вход второго звена, т.е. , а алгебраически складывается с .

Если вычитается из , т.е. , то связь отрицательна.

Итак, пусть первое звено охвачено вторым звеном, как отрицательной обратной связью. САР по отклонению это замкнутая система с отрицательной обратной связью. В простейшем случае (как в данном случае) ее можно рассматривать как систему, состоящую из двух звеньев: объекта регулирования и регулятора. Найдем передаточную функцию для САР по отклонению.

, т.к. .

Передаточные функции звеньев можно записать: ,

, но .

Тогда получим , откуда находим .

,

.

,

откуда

.

Таким образом, передаточная функция для САР по отклонению равна:

.

Итак, зная передаточные функции можно найти , а, в конечном счете, записать дифференциальное уравнение САР по отклонению.

Для структурной схемы из «n» последовательно соединенных звеньев , охваченных отрицательной обратной связью , передаточная функция САР будет иметь вид:

.

Пользуясь структурными схемами, можно синтезировать САР с заданными свойствами.

Устойчивость замкнутых САР

Устойчивыми являются линейные САР, в которых возможны только апериодические или колебательные затухающие переходные процессы.

Устойчивость САР зависит от сочетания динамических характеристик объекта и регулятора.

Динамические свойства линейной САР в общем случае описывается дифференциальным уравнением вида:

где а_i, b_i –постоянные величины (1).

Решение этого уравнения для заданной функции входного сигнала и «m» ее производных описывает переходный процесс в САР, вызванный действием этой функции.

А.М.Ляпунов доказал, что судить об устойчивости линейной динамической системы можно на основании анализа ее свободного движения, т.е. изменения выходного сигнала системы после снятия возмущающего воздействия. Если выходной сигнал системы при свободном движении возвращается к заданной величине, то такая система устойчива.

Свободное движение линейной САР описывается решением ее дифференциального уравнения (1) с правой частью, равной нулю.

(2)

Это уравнение в преобразованном по Лапласу виде называется характеристическим уравнением САР.

(3)

Анализ устойчивости линейной САР сводится к вычислению корней ее характеристического уравнения (3). Для устойчивости линейной САР необходимо и достаточно, чтобы все действительные корни характеристического уравнения системы или действительные части всех его компонентных корней были отрицательными.

Напомним, что в общем случае корни характеристического уравнения могут быть вещественными и комплексно-сопряженными.

,

где - вещественная часть корней, -мнимая часть корней. (Вещественные корни будем считать частным случаем комплексных при ).

Таким образом, могут иметь место случаи:

а) Устойчивая САР

б) САР на границе устойчивости

в) Неустойчивая САР

Таким образом, прямой путь определения устойчивости системы состоит в отыскании корней характеристического уравнения. Но этот путь трудоемкий, особенно при . Поэтому практически для анализа устойчивости применяют ряд косвенных оценок называемых критериями устойчивости. Эти оценки получены на основании необходимого и достаточного условия устойчивости. Они позволяют судить об устойчивости без вычисления корней ее характеристического уравнения.

Критерий устойчивости Рауса-Гурвица

Этот критерий относится к алгебраическим критериям устойчивости, накладывающим ограничения на коэффициенты характеристического уравнения.

Если в характеристическом уравнении , то для устойчивости САР необходимо и достаточно чтобы были положительными «n» определителей Гурвица: .

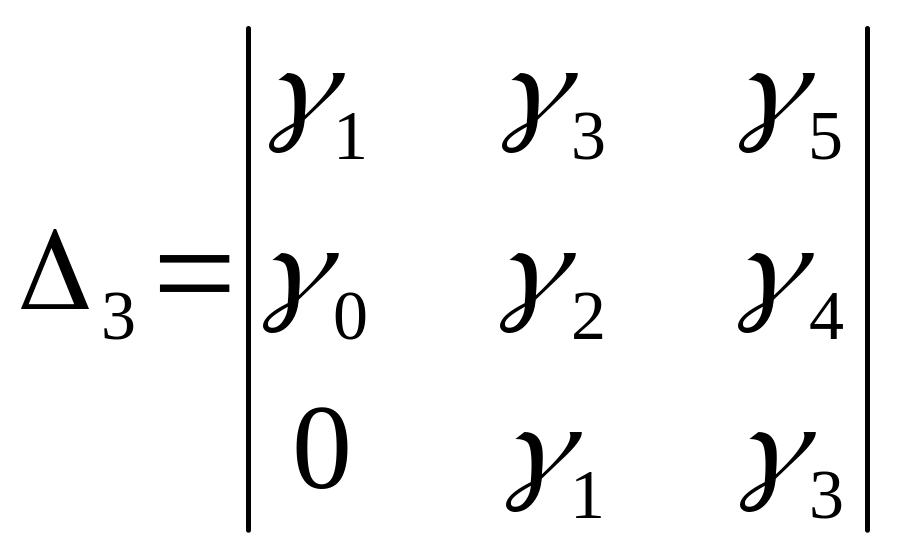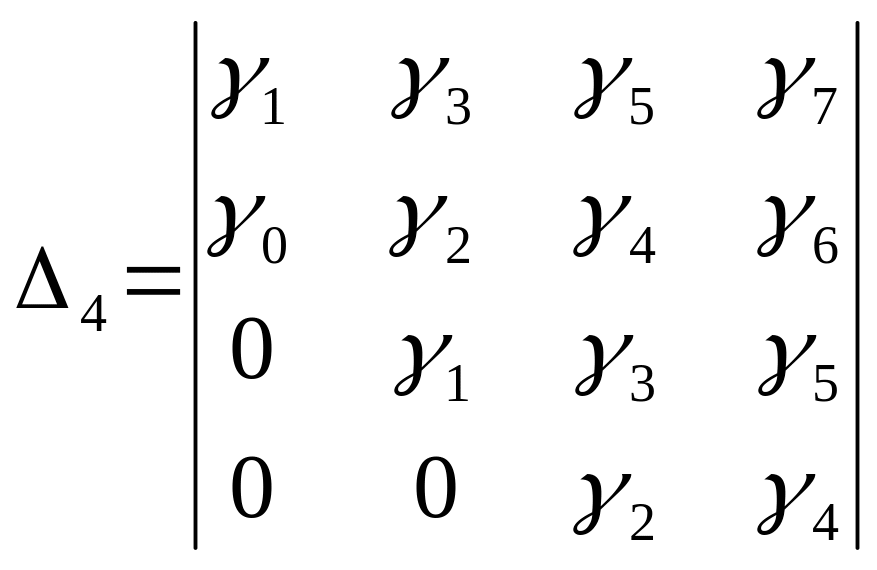; ; ; и т.д. до

При этом коэффициенты с индексом > степени «n» уравнения заменяются нулями. Если эти определители положительны [26], то все корни характеристического уравнения имеют отрицательную вещественную часть.

Пример: Проверить устойчивость САР, если характеристическое уравнение имеет вид:

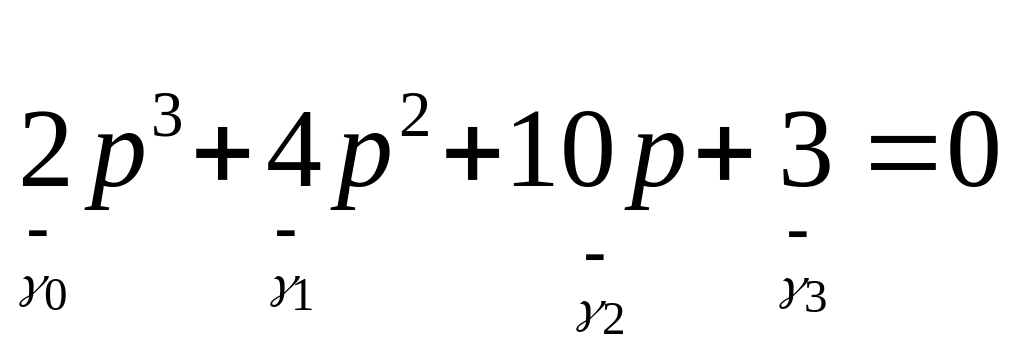
Другим способом .

Таким образом, так как , , то исследуемая САР устойчива.

Критерий устойчивости Рауса-Гурвича рационально применять для уравнений не выше 4-й-5-й степени. Есть также другие критерии устойчивости: Михайлова, Найквиста и т.д.