4. Колебательное звено

После скачкообразного изменения х_вх изменение х_вых имеет форму затухающих синусоидальных колебаний ( – коэффициент затухания, ).

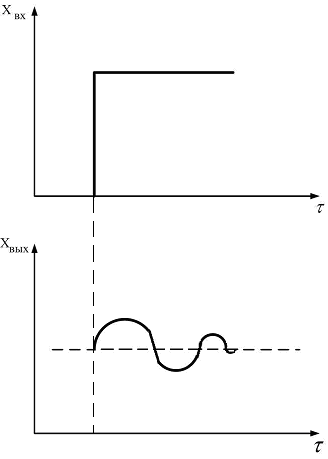
Рис. 2.10.

Звено описывается обыкновенным дифференциальным уравнением 2-го порядка:

,

где Т₁, Т₂, к – постоянные коэффициенты.

Решение уравнения имеет вид:

,

где ;

;

;

.

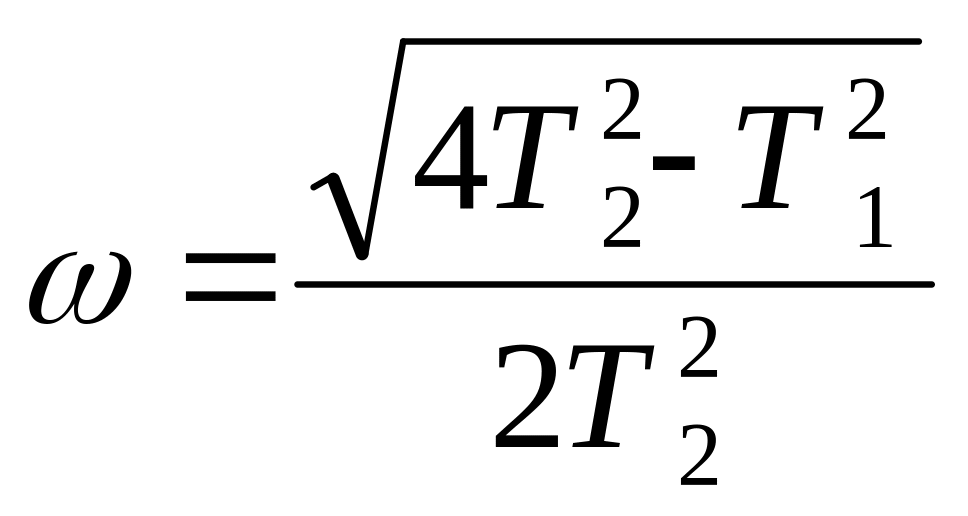В зависимости от значения  величина х_вых может совершать незатухающие колебания (=0), возрастающие колебания (<0), затухающие колебания (<1).

Примером звена (<1) является U-образная трубка.

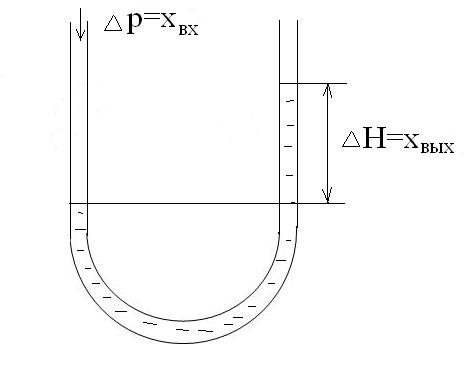
Рис. 2.11.

5. Апериодическое звено 2-го порядка

Зависимость в неустановившемся режиме для данного типа звена имеет вид:

,

где Т₁, Т₂, к – постоянные коэффициенты.

Решением данного уравнения является:

.

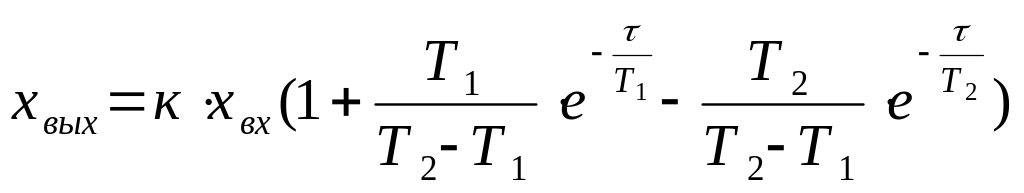
Величина х_вых с течением времени стремится к новому установившемуся значению без колебаний. Есть точка перегиба.

Пример.

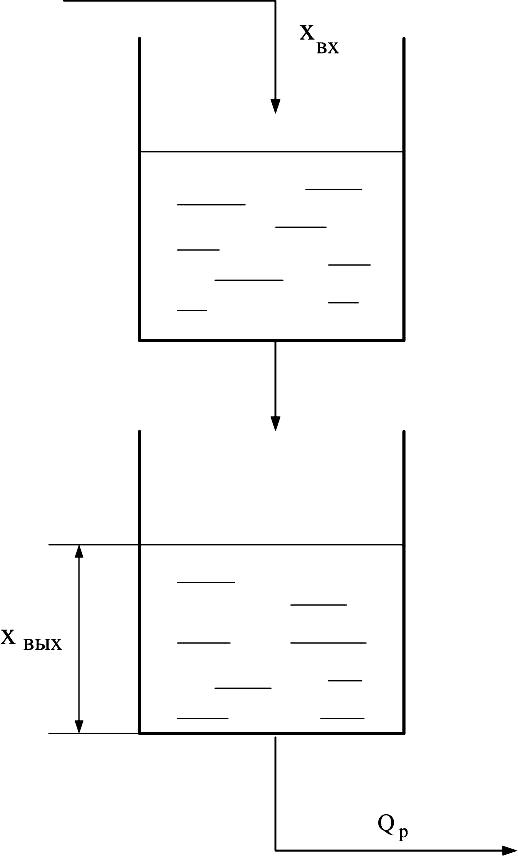
Рис. 2.12. Двухемкостный объект

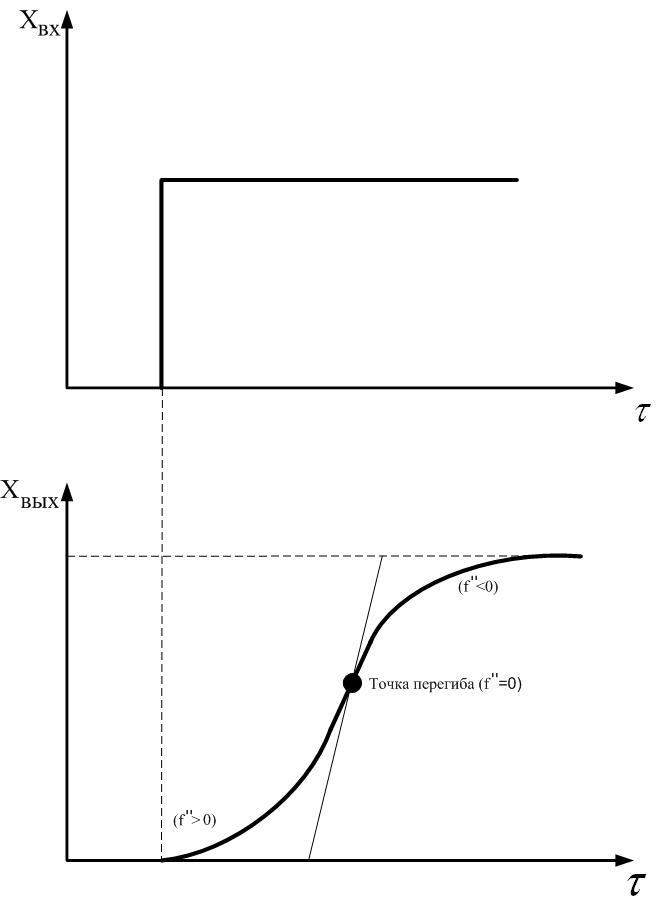
Рис. 2.13. Динамическая характеристика двухемкостного объекта

Уравнения колебательного и апериодического звена 2-го порядка имеют одинаковый вид. Как их отличить?

Пример:

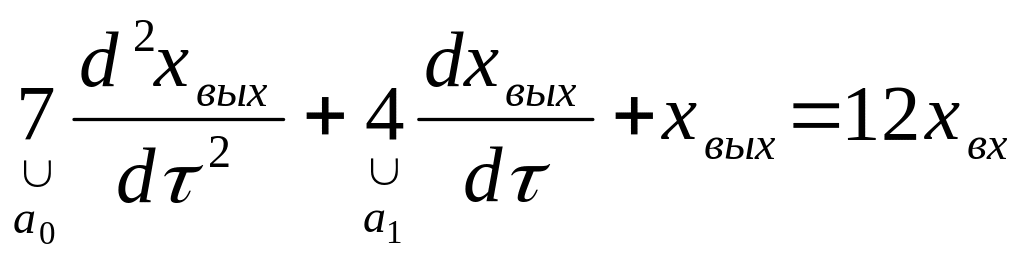
Если , то это апериодическое звено 2-го порядка;

– колебательное звено (как здесь 4²<47).

6. Дифференцирующее звено

У звена такого типа изменение х_вых пропорционально скорости изменения х_вх.

а) Идеальное дифференцирующее звено

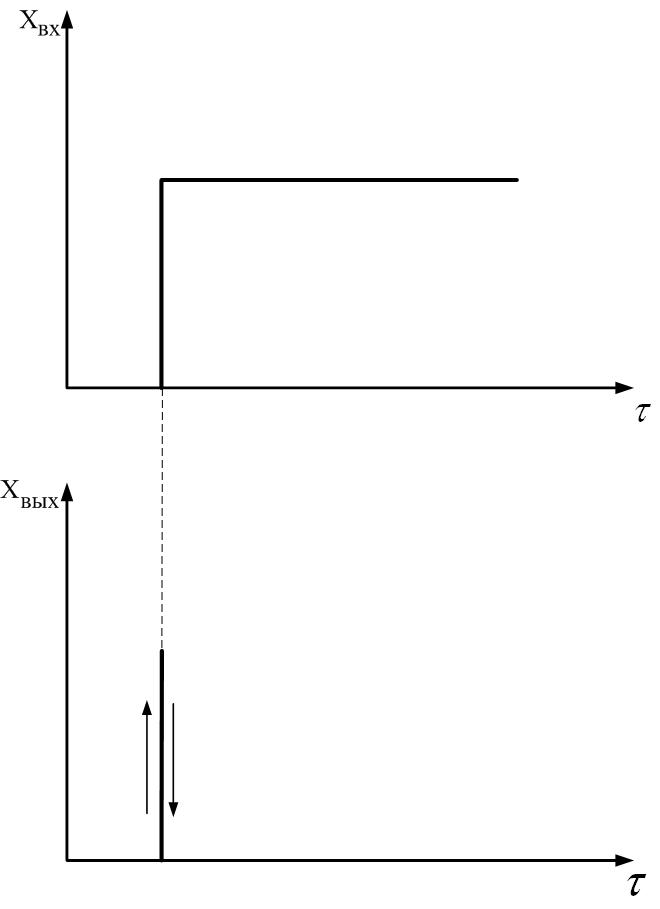
Рис. 2.14.

Величина х_вых в момент изменения х_вх меняется от 0 до  и снова возвращается к нулю.

б) Реальное дифференцирующее звено

;

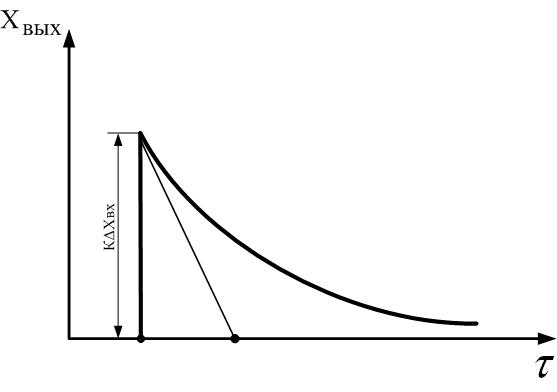
Рис. 2.15.

Т – постоянная времени.

Пример:

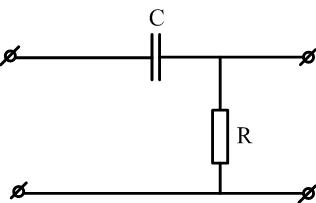
Рис. 2.16.

Конденсатор С зарядили мгновенно. Затем он постепенно разряжается через сопротивление: это RC цепочка – реальное дифференцирующее звено.

2.1.1. Необходимые сведения из операционного исчисления

Форма записи математической модели объекта (звена) может быть различной: алгебраические и трансцендентные уравнения, обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных. В некоторых случаях используются специальные формы записи, такие как передаточные функции, временные и частотные характеристики.

Для того, чтобы записать передаточную функцию звена необходимо использовать метод операционного исчисления.

Основной идеей этих методов является переход от исходного дифференциального уравнения к некоторому вспомогательному алгебраическому, при построении которого учитывается также система начальных условий.

Обратное преобразование от решения вспомогательного алгебраического уравнения позволяет получить требуемое частное решение первоначально заданного дифференциального уравнения.

Основным понятием операционного исчисления является преобразование Лапласа, которое ставит в соответствие функции действительной переменной f() (оригиналу), определенной при – изображение-функцию F(p), определенную равенством: ,

где р – положительное действительное число или комплексное число с положительной действительной частью.

Переход от оригинала f() к его изображению обозначается символами: или , а от изображения к оригиналу или .

Чтобы гарантировать существование изображения и сходимость всех используемых несобственных интегралов, достаточно предположить, что оригинал f() удовлетворяет следующим условиям:

1. На любом конечном интервале функции f() и f’() имеют не более конечного числа точек разрыва 1-го рода (конечных скачков);

2. f()  0 для <0;

3. f() растет не быстрее показательной, т.е. существуют такие действительные постоянные М>0, S>0, что .

Существуют правила для преобразования Лапласа, которые используются при решении дифференциальных уравнений [25].

Вот некоторые из правил, которые потребуются:

Дифференцирование оригинала

Пусть f() дифференцируема на и f’() удовлетворяет условиям 1-3 существования изображения. Тогда:

а) если , то ; в частности, если , то , т.е. дифференцированию функции соответствует умножение изображения на «р».

б) если существует и удовлетворяет условиям 1-3, то из следует . В частности, если удовлетворяет нулевым начальным условиям , то

.

Таким образом, при переходе к изображениям и при соблюдении нулевых начальных значений с оператором дифференцирования можно обращаться как с обычным множителем «р».

Интегрирование оригинала

Пусть непрерывна на , удовлетворяет условиям 1-3 существования изображения и .

Тогда , т.е. интегрирование функции соответствует деление изображения на «р».

Временной оператор – Р

Передаточная функция – W(P)

Динамические свойства звеньев САР, а также САР в целом часто удобнее представлять не дифференциальными уравнениями, а так называемыми передаточными функциями . В дальнейшем будем обозначать и как и .

Передаточная функция рассматривается как условная запись дифференциального уравнения, в котором временной оператор обозначен буквой Р, т.е. . В результате передаточные функции условно рассматриваются как алгебраические выражения (взамен дифференциальных). Это облегчает и упрощает анализ полученных выражений при математических выкладках, связанных с изучением САР.

Получим передаточные функции для вышеназванных типовых динамических звеньев.