5. Задание № 5 «исследование процесса дискретизации аналоговых сигналов»

5.1. Условие

Аналоговый сигнал s(t) (см. рис. 5.1) длительностью T_с= 1мс подвергнут дискретизации путем умножения на последовательность δ-импульсов. Интервал дискретизации Т_д.

Требуется:

1) Рассчитать и построить график зависимости модуля спектральной плотности аналогового сигнала s(t) от частоты (спектрограмму модуля).

2) Определить максимальную частоту в спектре аналогового сигнала f_m, ограничив спектр в соответствии с одним из известных критериев.

3) Рассчитать интервал дискретизации Т_д и число выборок N.

4) Рассчитать отсчеты аналогового сигнала s(kТ_д) и изобразить и под временной диаграммой аналогового сигнала в едином временном масштабе.

5) Записать выражение для дискретного сигнала s_T(t) и определить спектральную плотность этого сигнала.

6) Провести прямое дискретное преобразование Фурье (ДПФ) и определить коэффициенты ДПФ.

7) На одном рисунке друг под другом в едином частотном масштабе построить: спектрограммы модулей: исходного аналогового сигнала; сигнала с ограниченным спектром; дискретного сигнала; коэффициентов ДПФ.

8) Записать выражение для z-преобразования дискретного сигнала, приведя его к рациональной дроби.

5.2 Исходные данные

Изобразим заданный сигнал на рис.5.1.

Рис. 5.1 — Заданный аналоговый сигнал

5.3. Решение

5.3.1. Для начала зададим заданный сигнал аналитически

Определим спектральную плотность сигнала применяя ППФ [1]:

Поскольку отличен от нуля в пределах , поэтому пределы интегрирования можно ограничить.

Проведем численное интегрирование с помощью пакета MathCAD [3] и построим график спектрограммы модуля.

Рис. 5.2 — Спектрограмма модуля аналогового сигнала

Из спектрограммы модуля определим . Для этого на уровне 0,1 проведем прямую и, в точке, где пересекается прямая и спектрограмма модуля и будет .

Рис. 5.3 — Спектрограмма модуля аналогового сигнала и прямая на уровне 0,1

Выберем Тогда количество выборок [1]:

5.3.4. Рассчитаем отсчеты аналогового сигнала.

Для этого вместо t в формуле (5.1) подставим .

Рассчитаем по формуле (5.7) и составим таблицу отсчетных значений.

Таблица 5.1 — Значения высоты отсчетов

	0	1	2	3	4	5	6	7	8
	0	0,659	0,435	0,287	0,189	0,125	0,082	0,054	0

Построим отсчеты аналогового сигнала.

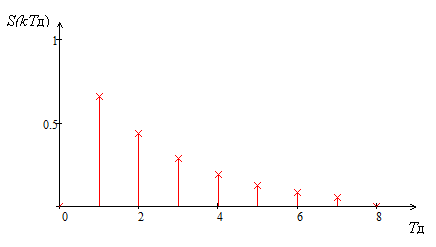
Рис. 5.4 — Временная диаграмма аналогового сигнала и его отсчеты

5.3.5. Запишем выражение для дискретного сигнала s_T(t) и определим спектральную плотность этого сигнала.

Запишем аналитическое выражение для сигнала c ограниченной спектральной плотностью (рис. 5.5, а) [1].

По формуле (5.8) построим график ограниченной спектральной плотности сигнала (рис. 5.5, b)

Количество выборок конечно, значит аналоговый сигнал также конечен во времени, следовательно, дискретный сигнал в общем виде запишется так

Используя фильтрующее свойство δ-функции, выражение представим в следующем виде:

По формуле (5.10) построим график спектральной плотности дискретного сигнала (рис. 5.5, c)

5.3.6. Проведём прямое дискретное преобразование Фурье (ДПФ) и определим коэффициенты ДПФ.

Дискретное преобразование Фурье (ДПФ) определяется по формуле [1]:

где n=0, 1, …, N — номер отсчета спектральной плотности.

Подставим значения из таблицы 5.1 и получим:

Отсчеты спектральной плотности, определяемые (5.11), следуют через интервалы Взяв модули коэффициентов ДПФ построим спектрограмму, разместив отсчёты на оси частот через интервалы, кратные .

Рис. 5.5 — Графики модуля спектральной плотности исходного аналогового сигнала (a) и сигнала с ограниченным спектром (b), дискретного сигнала (c), коэффициентов ДПФ (d)

5.5.6. Запишем выражение для z-преобразования дискретного сигнала и приведём его к рациональной дроби.

Проведем z-преобразование дискретного сигнала, которое определяется соотношением [1]:

где — комплексная переменная, которая вводится как Вычислим сумму (5.16), подставив найденные выше значения дискретного сигнала

5.4. Выводы

В ходе выполнения задания № 5 была рассчитана спектральная плотность аналогового входного сигнала. Определена максимальная частота в спектре входного сигнала f_m=3,5 кГц. Рассчитан интервал дискретизации и определено число выборок. и N=9.Определена спектральная плотность дискретного сигнала. Проведено ДПФ. Построены соответствующие графики. Записано выражение для z-преобразования дискретного сигнала.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Учебное пособие «Сигналы и процессы в радиотехнике, часть 2» для студентов направления 6.050901 — «Радиотехника» / СевНТУ; сост. Ю. Б. Гимпилевич — Севастополь: СевНТУ, 2013. — 149 с.

2.Методические указания «Методические рекомендации к выполнению курсовой работы по дисциплине «Сигналы и процессы в радиотехнике» для студентов дневной формы обучения направления 6.050901 — «Радиотехника» / СевНТУ; сост. Ю.Б. Гимпилевич, И.В. Сердюк — Севастополь: СевНТУ, 2013. — 24 с.

3.Программный пакет для математических расчетов «Mathcad 14».